1 条题解
-
0
自动搬运
来自洛谷,原作者为

chinuya
欲买桂花同载酒,终不似,少年游。搬运于
2025-08-24 22:04:34,当前版本为作者最后更新于2022-08-24 00:17:00,作者可能在搬运后再次修改,您可在原文处查看最新版自动搬运只会搬运当前题目点赞数最高的题解,您可前往洛谷题解查看更多
以下是正文
为了纪念第一道蓝题,特来写一篇题解。
2022.8.25:更改了 LaTeX 格式。
直奔主题:
思路:
显然的,当有一个矩阵满足:
- 左上角坐标为 ,右下角坐标为
则这个矩阵的最优解为:
- 将这个矩阵切开(横、竖)后的两个矩阵的最优解中的最小值与这个矩阵的各元素之和。
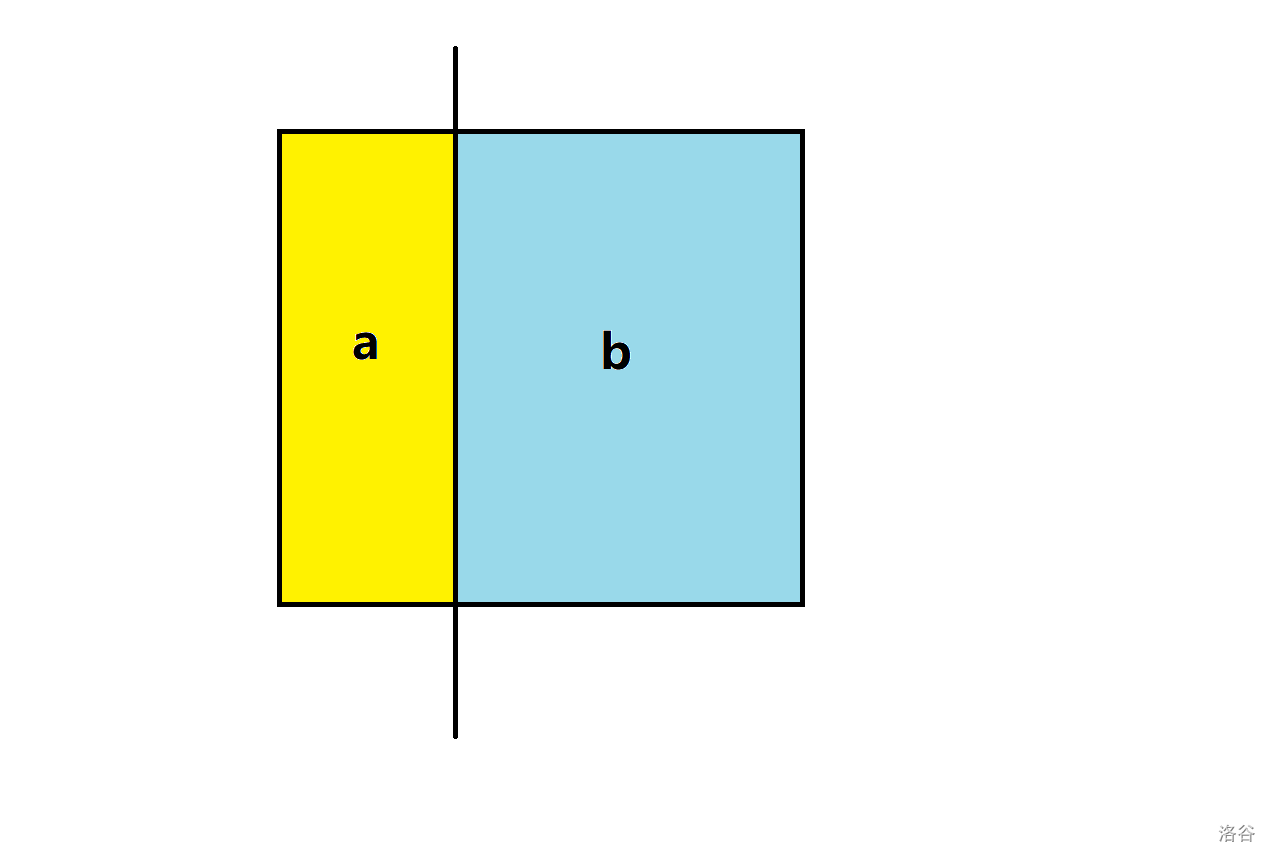
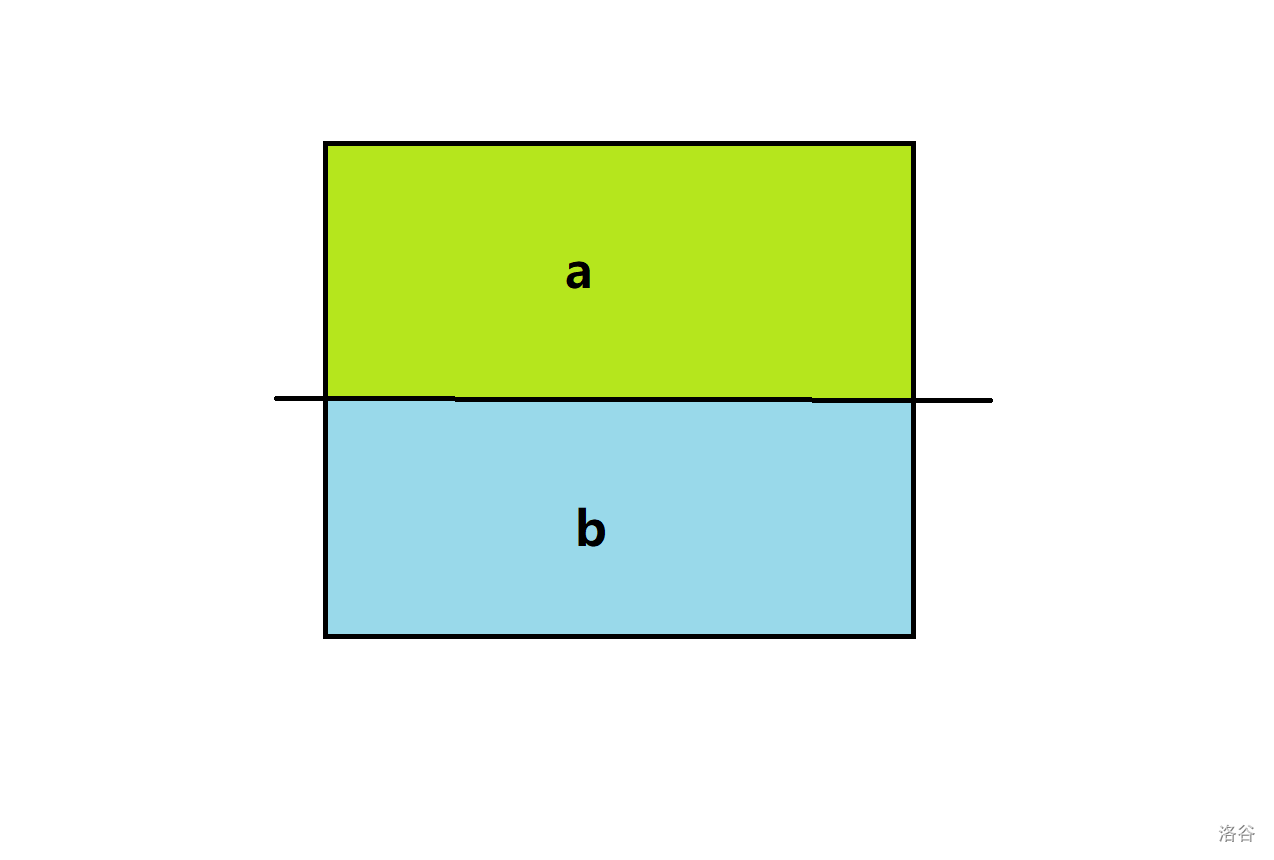
如上,是横着切和竖着切的两种情况。
所以,我们可以 dfs 枚举每一刀切的位置。同时,用记忆化删去部分冗余的计算。定义一个数组 进行记忆化搜索。
代码:
#include<bits/stdc++.h>//支持万能头文件!! using namespace std; int n,m; int ra[60][60]; //每块巧克力上的葡萄干数量 int f[60][60][60][60]; //记忆化 int dfs(int a,int b,int c,int d) { if(f[a][b][c][d]!=0)//如果已经切过这种情况了 return f[a][b][c][d];//直接返回 if(b==d&&a==c) return 0;//如果开始点和结束点是同一点,即没法切了,就return int ma=1e10;//赋一个极大值,以便后来作min运算 for(int i=a;i<c;i++) ma=min(ma,dfs(a,b,i,d)+dfs(i+1,b,c,d));//横着切,即上边加下边 for(int i=b;i<d;i++) ma=min(ma,dfs(a,b,c,i)+dfs(a,i+1,c,d));//竖着切,即左边加右边 for(int i=a;i<=c;i++) for(int j=b;j<=d;j++) ma+=ra[i][j];//要付出多少葡萄干 return f[a][b][c][d]=ma; /*等价于: f[a][b][c][d]=ma; return f[a][b][c][d];*/ } int main() { cin>>n>>m; for(int i=1;i<=n;i++){ for(int j=1;j<=m;j++){ cin>>ra[i][j]; //循环输入葡萄干 } } cout<<dfs(1,1,n,m); return 0; }这种做法开 O2 就可以 AC 了,
但是,作为一个合格的 oier ,我们应该不断追求更好的做法。优化思路:
因为考虑到每进行一次 dfs,就要算一遍葡萄干的和,所以很自然地想到利用前缀和数组来优化。
每输入一个数,则对其进行前缀和计算。就避免每次搜索都用一个双层循环来计算。
前缀和代码:
AC代码:
#include<bits/stdc++.h>//支持万能头文件!! using namespace std; int n,m; int ra[60][60]; //每块巧克力上的葡萄干数量 int f[60][60][60][60]; //记忆化 int cc[60][60]; //前缀和数组 int dfs(int a,int b,int c,int d) { if(f[a][b][c][d]!=0)//如果已经切过这种情况了 return f[a][b][c][d];//直接返回 if(b==d&&a==c) return 0;//如果开始点和结束点是同一点,即没法切了,就return int ma=1e10; for(int i=a;i<c;i++) ma=min(ma,dfs(a,b,i,d)+dfs(i+1,b,c,d));//横着切,即上边加下边 for(int i=b;i<d;i++) ma=min(ma,dfs(a,b,c,i)+dfs(a,i+1,c,d));//竖着切,即左边加右边 f[a][b][c][d]=ma+cc[c][d]-cc[a-1][d]-cc[c][b-1]+cc[a-1][b-1]; //这里使用前缀和优化 return f[a][b][c][d]; } int main() { cin>>n>>m; for(int i=1;i<=n;i++){ for(int j=1;j<=m;j++){ cin>>ra[i][j]; //循环输入葡萄干 cc[i][j]=ra[i][j]+cc[i][j-1]+cc[i-1][j]-cc[i-1][j-1];//计算前缀和 } } cout<<dfs(1,1,n,m); return 0; }这样不用 O2 就可以过了!
拓展:
不会吧不会吧,不会还有人不知道二维前缀和怎么算吧!
核心代码:
其中, 表示前缀和数组, 表示原数组。
我们可以用一个图形来理解一下:
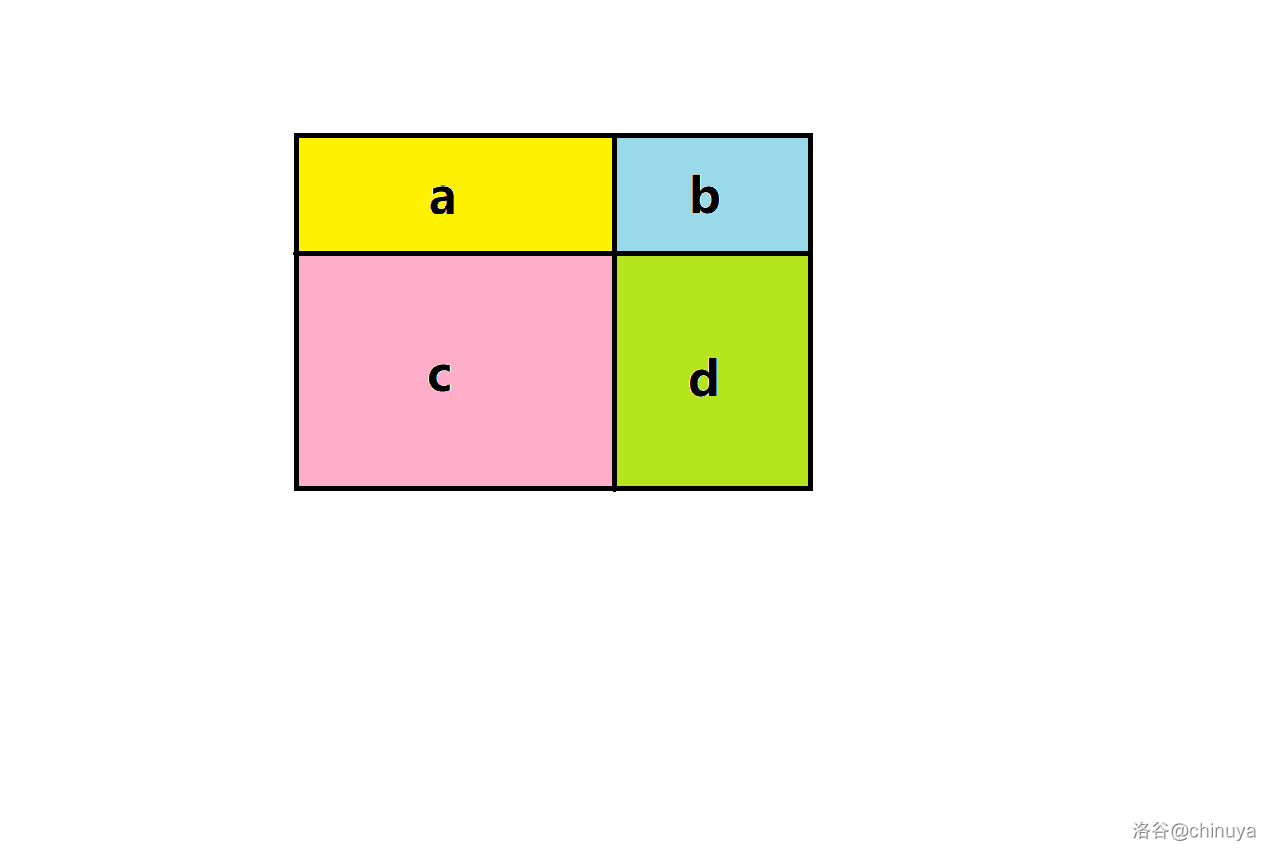 整个面积就是 , 相当于 , 相当于 , 相当于 ,相当于。
整个面积就是 , 相当于 , 相当于 , 相当于 ,相当于。很显然:
$$\begin{aligned} s_{i,j} &=a+b+c+d \\ &=(a+b)+(a+c)-a+d \\ &=s_{i-1,j}+s_{i,j-1}-s_{i-1,j-1}+k_{i,j} \end{aligned} $$当然,这不是严谨的推论,图也不标准,仅供参考。
- 1
信息
- ID
- 3872
- 时间
- 5000ms
- 内存
- 128MiB
- 难度
- 5
- 标签
- 递交数
- 0
- 已通过
- 0
- 上传者
