自动搬运

查看原文

来自洛谷，原作者为

	zhylj 人生输家

搬运于2025-08-24 21:55:28，当前版本为作者最后更新于2018-03-17 16:37:15，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

想要更好的阅读体验？前往我的博客：https://www.cnblogs.com/zhylj/p/9525885.html

首先，我们考虑最暴力的方法：

对于每组换乘站，有$8$种情况：

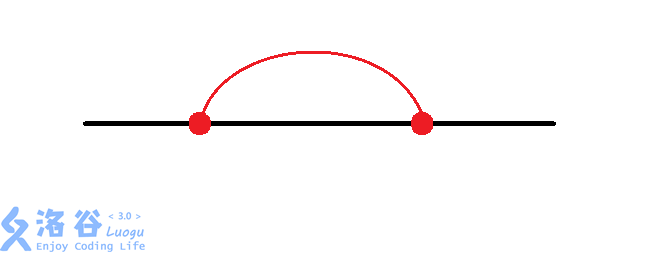
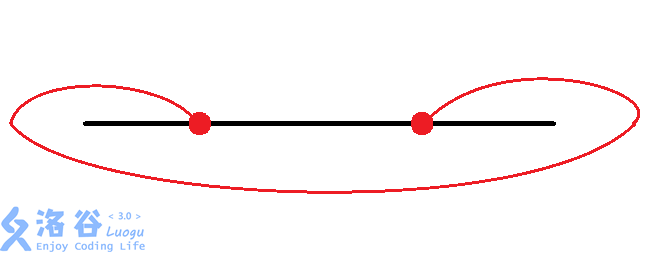
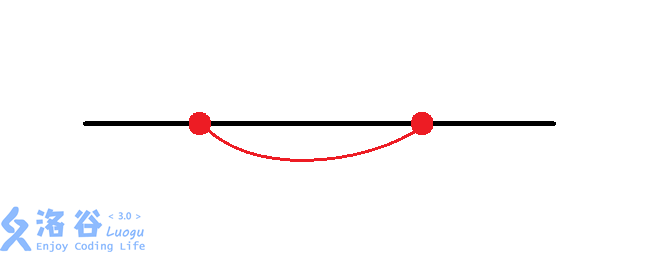
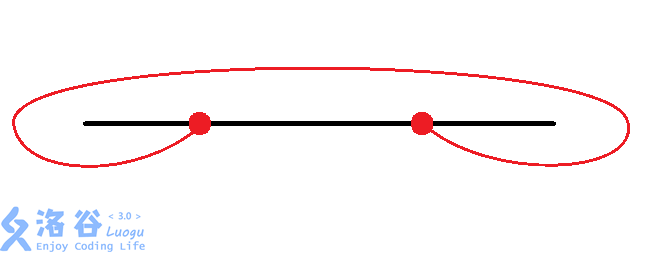
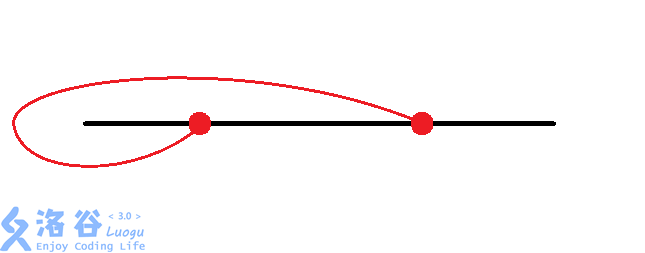
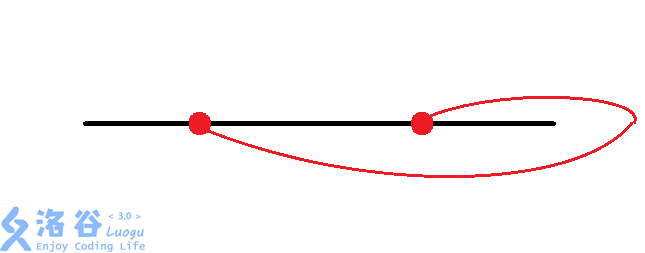
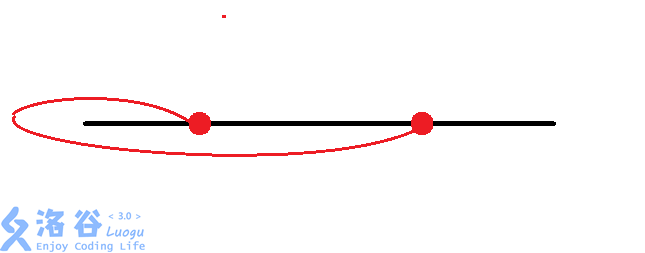
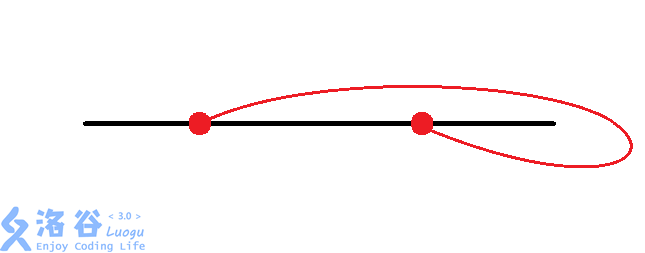
考虑我们对每组换乘站进行枚举，再加上$O(n)$的暴力找交点数，时间复杂度为$O(n8^{\left(\frac{n}{2}\right)})$，面对$n\le 44$的数据，显然会$\rm TLE$。

期望得分$\rm 10$。

考虑寻找这$8$种情况有没有重复。

我们发现，对于前两种，放到一起，会是这样的：

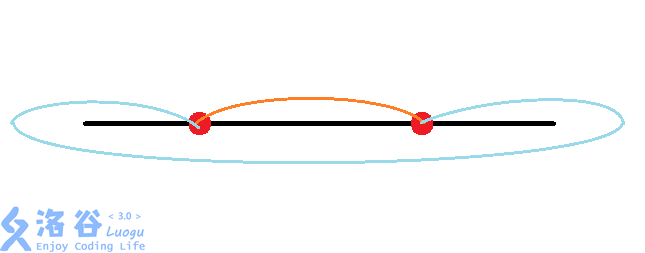
对于这种情况，由于这两条线产生了一个完全包住0号线的环，我们发现对于每一个其他的线，要么不和这两条线产生交点，要么对这两条线每条都产生一个交点。

故，每个点不需要枚举左右，只需要枚举上下即可，时间复杂度$O(4^{(\frac{n}{2})}\times n)$
情况还剩下：

再考虑，能不能继续减少情况数。

于是我们考虑把前两幅图的放在一起。

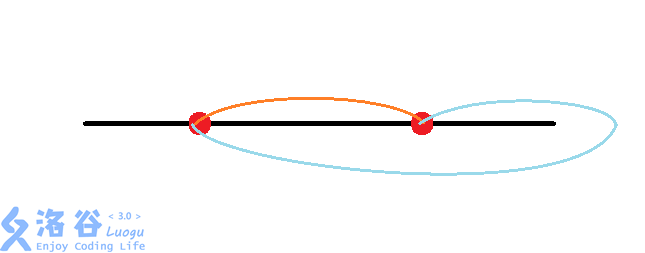
这张图也构成了环，但是这个环并没有能把0号线包住，但是这个环把0号线右边的所有点包住了，也就是在第一个红点右边的所有点是不会受到这两个的选择的影响的。

然后再来看第一个红点左边的情况，如果你是按左端点从左往右搜索的，你会发现到这步的时候红点左边已经搜索完了，即在左边会进出环的点已经全部决定了，而又因为不会对右边造成影响，所以我们可以贪心地取这两条环产生交点的最小值。

同理，剩下的也可以这样处理。

时间复杂度$O(n2^{\left(\frac{n}{2}\right)})$。

期望得分$\rm 80$分。

搜索的时间复杂度看上去已经很优了，所以我们考虑能不能优化找交点的时间复杂度。

考虑我们从左往搜索，用$a.l,a.r$表示$a$线路的左端点右端点，若只考虑同向，因为$a.l \lt a.r,\;b.l \lt b.r,\; a.l \lt b.l$则有三种情况：

显然，只有情况$3$是相交的。

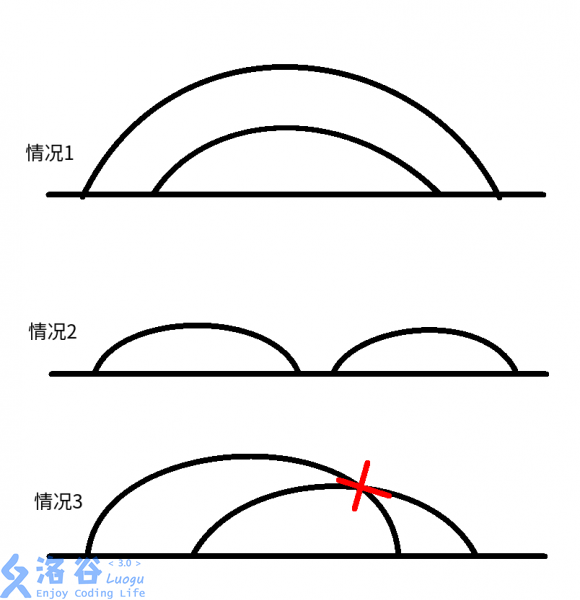
我们发现只有$b.l\lt a.r\lt b.r$我们才需要统计。

是不是很熟悉？你可以使用树状数组来进行统计。

每个右端点标记$1$，然后求$[b.l,b.r]$的和即可。

对于朝向问题，显然左端点的朝向不影响，右端点只有同向才会相交，可以自行画图，这边不作演示。

至于代码，由于写的时候比较早，太丑就不放出来了。

时间复杂度$O(2^{\left(\frac{n}{2}\right)}\log n)$，可以$\rm AC$。

有问题请留言。