自动搬运

查看原文

来自洛谷，原作者为

	Supor__Shoep AFO | 耳畔之际，恋之回音。 | 你的她，青春永驻

搬运于2025-08-24 22:51:00，当前版本为作者最后更新于2023-08-25 08:03:23，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

---

这里是出题人题解。本题有较多奇怪做法，这里就介绍一下我初步想到的解法。

下文定义 $cnt$ 为基环数上的环的大小。

Subtask 1:

枚举两个点 $x,y$，通过搜索得到 $x\to y$ 的路径（保证翻转的边数尽可能小），记录翻转的边和未翻转的边，然后乘起来就可以得到答案。

枚举是 $O(n^2)$，找路径在最坏情况下是 $O(n)$，因此总时间复杂度约为 $O(n^3)$。

期望得分：$5pts$

Subtask 2:

枚举每一个点依次算答案。

我们从枚举的点 $x$ 开始进行搜索，并时刻记录两个乘数的值。当搜索到了基环树的环时，我们只能按照有向边的方向走，如果你反着走，就没有保证翻转了最少的边。

遍历完整棵树，把所有答案累加到 $x$ 的答案上面。时间复杂度 $O(n^2)$。

期望得分：$5pts+10pts=15pts$

Subtask 3:

这个做法和正解已经非常接近了！！！！！

剖析一下基环树的结构，我们可以将其理解为一个环以及以环上节点为根的许多棵树形成的集合。为了方便表示，树表示以环上节点为根的树，基环树才表示整个集合。因此尝试分类讨论：

• 环上节点：我们发现任意两个环上节点并不会互相产生代价，也就是说只有树上的某些节点会对环上节点产生代价。考虑预处理出每一棵树中，离根节点至少 $k$ 条边的所有点到根节点的距离之和。设一棵树 $T$ 中的距离之和为 $w_0$，某个环上节点 $x$ 到 $T$ 的根节点的距离为 $w_1$，则 $T$ 带给 $x$ 的答案的代价就是 $w_0\times w_1$。因此环上节点的答案就可以用 $O(cnt^2)$ 求了。

• 不同树上的节点：如果两个节点在不同的树中，那么它们两个可能会产生代价。不难发现这里的思路与上一种情况类似，设一棵树为 $T$，$T$ 的根节点答案为 $w_0$，考虑从根节点向下进行搜索（注意是在反图上面搜索），每次深度增加一个边权 $val$ 的时候，只有未翻转的边权之和在发生改变，已翻转的边权之和是不会变的，因此树上节点的答案可以根据其父亲节点的答案推来，并且 $\Delta=\Delta val\times D$，其中 $D$ 表示已翻转的边权之和，是非常好求的。

• 同一棵树上节点：这是一部分人容易忽略的一种情况。我们可以通过枚举 $x$ 来计算 $x$ 对其它节点的影响代价。首先我们发现单个枚举 $x$ 肯定不行，于是我们将枚举的 $x$ 换一个含义，它代表的是以 $x$ 为根的子树。我们找到 $x$ 向上的 $k$ 级祖先 $y$，如果找不到，则说明 $x$ 不会给同一棵树中的节点带来代价，那么整棵子树也就不能带来完整的代价。否则，$x\to y$ 的路径就相当于已翻转的边权之和，如下图所示，$k=1$，红色部分表示枚举的子树，而蓝色的部分就是这棵子树送出代价的范围。

  现在我们要将 $x$ 的子树中所有节点的答案传到其它节点。设 $x$ 的 $k$ 级祖先为 $y$，记 $R$ 表示 $x$ 中所有节点到 $y$ 的距离之和，$dis_i$ 表示 $i$ 到根节点的距离，则对于蓝色部分的所有节点 $p$，答案增加 $R\times (dis_p-dis_y)$，把式子拆开变成 $R\times dis_p-R\times dis_y$。这里的 $dis_p$ 取自于蓝色部分，而不属于红色部分，考虑用差分维护 $\sum R$ 和 $\sum R\times dis_y$。最后计算答案的时候从根开始，向下将差分值进行累加即可。

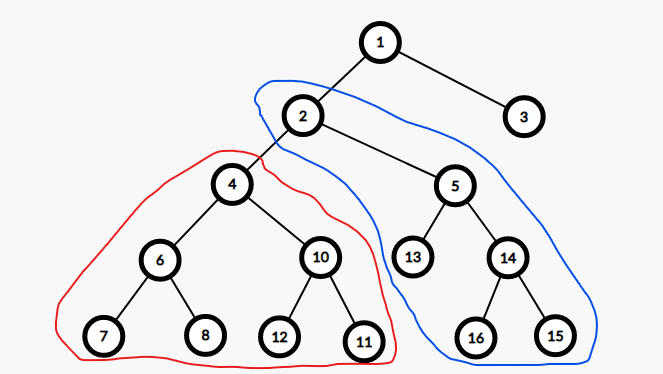
计算环上的答案时，我们采用了 $O(cnt^2)$ 的枚举法，计算树上答案时，我们采用了 $O(nk)$ 的差分法，两者并列，时间复杂度 $O(\max\{nk,cnt^2\})$。

期望得分：$5pts+10pts+25pts=40pts$

Subtask 4:

在 $O(\max\{nk,cnt^2\})$ 的做法中，我们发现如果 $cnt$ 很大，那么还是会超时，而树上差分的方法是 $O(nk)$，可以继续采用。所以我们只需要优化环上的答案就行了。

不难发现环上每一个节点的答案之间都有一些联系，考虑设计一个动态规划求解。

设 $dp_i$ 表示环上节点 $i$ 的答案，这种状态下没有办法进行初始化，因此先暴力枚举出任意一个点的答案。设 $D_i$ 表示以环上节点 $i$ 为根的树中深度大于 $k$ 的节点到 $i$ 的距离之和（$i$ 的深度为 $1$）。

给一个图：

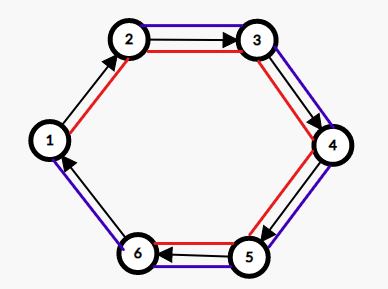
假如我们枚举的是 $1$ 号点，得到了答案 $dp_1$，红色线条对应的就是 $1$ 号点的答案所统计到的范围，而它本身不需要被计算，因为其中一个乘数变成了 $0$。按照顺序，现在我们要计算 $dp_2$，蓝色线条对应的是 $2$ 号点的答案应该统计到的范围。不难观察到它们都有一段重复的范围，即 $[2,6]$，除去不会被计算到的 $2$ 号点本身，区间范围 $[3,6]$ 的 $\sum D_i$ 是重复的，因此 $2$ 不必再枚举这一段的乘数。设 $dis(i,j)$ 表示 $i\to j$ 的距离（距离是指走有向边的距离），我们可以列出两者答案的式子：

$$dp_1=\sum _{j=2} ^6 dis(1,j)\times D_j$$ $$dp_2=(\sum _{j=3}^6 dis(2,j)\times D_j)+dis(2,1)\times D_1 $$

根据上图可以发现 $dis(1,j)-dis(2,j)$ 正是边 $(1,2)$ 的边权，则：

$$\begin{aligned} dp_2&=(\sum_{j=3}^6 (dis(1,j)-dis(1,2))\times D_j)+dis(2,1)\times D_1 \\ &=(\sum_{j=3}^6 dis(1,j)\times D_j)-dis(1,2)\times (\sum_{j=3}^6 D_j)+dis(2,1)\times D_1\\ &=dp_1-dis(1,2)\times D_2-dis(1,2) \times(\sum_{j=3}^6 D_j)+dis(2,1)\times D_1\\ &=dp_1-dis(1,2)\times (\sum_{j=2}^6 D_j)+dis(2,1)\times D_1 \end{aligned}$$

由于 $D_j$ 的值不变，所以我们可以提前预处理 $sum=\sum _{j=1}^{cnt} D_j$，同时还可以预处理出一个前缀和，方便计算 $dis$。设 $pre$ 表示环上节点 $i$ 的上一个环上节点，则：

$$dp_i=dp_{pre}-dis(pre,i)\times (sum-D_{pre})+dis(i,pre)\times D_{pre} $$

差分 $O(nk)$，动态规划 $O(cnt)$，时间复杂度 $O(nk)$。

期望得分：$5pts+10pts+25pts+60pts=100pts$

标程：

#include <bits/stdc++.h>
using namespace std;
const int MAXN = 1e6 + 5;
int head[MAXN], nxt[MAXN], to[MAXN], val[MAXN], tot;
void add(int x, int y, int z) {
    to[++tot] = y;
    val[tot] = z;
    nxt[tot] = head[x];
    head[x] = tot;
}
vector<pair<int, int> > v[MAXN];
int n, k;
void read(int &x) {
    x = 0;
    short flag = 1;
    char ch = getchar();
    while (ch < '0' || ch > '9') {
        if (ch == '-')
            flag = -1;
        ch = getchar();
    }
    while (ch >= '0' && ch <= '9') {
        x = (x << 1) + (x << 3) + (ch ^ 48);
        ch = getchar();
    }
    x *= flag;
}
long long D[MAXN];
int vv[MAXN], vis[MAXN], stk[MAXN], cnt;
int dfs1(int x) {//找环 
    if (vv[x] == 1) {
        vv[x] = 2, vis[x] = 1, stk[++cnt] = x;
        return 1;
    }
    vv[x] = 1;
    for (int i = head[x]; i; i = nxt[i]) {
        if (dfs1(to[i])) {
            if (vv[x] != 2) {
                vis[x] = 1, stk[++cnt] = x;
                return 1;
            }
            return 0;
        }
    }
    return 0;
}
int now, len[MAXN];
void dfs(int x, int dep, long long sum) {
    if (dep >= k)
        D[now] += sum;//更新 D[i] 的值 
    for (int i = 0; i < len[x]; i++) {
        if (vis[v[x][i].first])
            continue;
        dfs(v[x][i].first, dep + 1, sum + v[x][i].second);
    }
}
long long res[MAXN], dis[MAXN];
int temp[MAXN];
long long Dis[MAXN];
long long sum;
void dfs2(int x) {
    for (int i = 0; i < len[x]; i++) {
        if (vis[v[x][i].first])
            continue;
        res[v[x][i].first] = res[x] + sum * v[x][i].second, Dis[v[x][i].first] = Dis[x] + v[x][i].second;
        dfs2(v[x][i].first);
    }
}
int Get(int x, int dep) {//求 x 的 dep 级祖先 
    int rsum = dep;
    while (rsum--) {
        if (vis[x])
            return -1;
        x = to[head[x]];
    }
    return x;
}
long long sumup[MAXN], siz[MAXN];//sumup[i] 表示 i 的子树中所有点到 i 的距离之和，siz[i] 表示子树大小 
long long cf1[MAXN], cf2[MAXN];//分别维护 R 和 R * dis[y] 的和 
void dfs3(int x) {
    siz[x] = 1;
    for (int i = 0; i < len[x]; i++) {
        if (vis[v[x][i].first])
            continue;
        dfs3(v[x][i].first);
        siz[x] += siz[v[x][i].first], sumup[x] += 1ll * siz[v[x][i].first] * v[x][i].second + sumup[v[x][i].first];
    }
    int ancestor2 = Get(x, k - 1), ancestor = Get(ancestor2, 1);
    if (ancestor == -1)
        return;
    long long rsum = siz[x] * (Dis[x] - Dis[ancestor]) + sumup[x];//求出 R 
    cf1[ancestor] += rsum, cf1[ancestor2] -= rsum;//差分 
    cf2[ancestor] += rsum * Dis[ancestor], cf2[ancestor2] -= rsum * Dis[ancestor];
}
void dfs_down(int x) {//向下累加差分值并统计答案 
    for (int i = 0; i < len[x]; i++) {
        if (vis[v[x][i].first])
            continue;
        cf1[v[x][i].first] += cf1[x], cf2[v[x][i].first] += cf2[x];
        dfs_down(v[x][i].first);
    }
    res[x] += Dis[x] * cf1[x] - cf2[x];
}
int main() {
    read(n), read(k); 
    for (int i = 1; i <= n; i++) {
        int x, y, z;
        read(x), read(y), read(z);
        add(x, y, z), v[y].emplace_back(x, z);
        len[y]++;
    }
    dfs1(1);
    for (int i = 2; i <= cnt; i++) temp[i] = stk[i];
    for (int i = 2; i <= cnt; i++) stk[i] = temp[cnt - i + 2];//处理完之后，stk[i] 就表示第 i 个环上节点 
    for (int i = 1; i <= cnt; i++) now = i, dfs(stk[i], 0, 0);//求出 D[i] 
    for (int i = 2; i <= cnt; i++) dis[i] = dis[i - 1] + val[head[stk[i - 1]]];//预处理前缀和 
    dis[cnt + 1] = dis[cnt] + val[head[stk[cnt]]];
    for (int i = 2; i <= cnt; i++) sum += D[i], res[stk[1]] += dis[i] * D[i];//预处理 D[i] 的和，并暴力枚举第一个点的答案 
    for (int i = 2; i <= cnt; i++) {
    	int wx = val[head[stk[i - 1]]];
    	res[stk[i]] = res[stk[i - 1]] + (dis[cnt + 1] - wx) * D[i - 1] - sum * wx;//转移 
        sum -= D[i], sum += D[i - 1];
    }
    sum += D[cnt];
    for (int i = 1; i <= cnt; i++) sum -= D[i], dfs2(stk[i]), sum += D[i];//向树上传递答案 
    for (int i = 1; i <= cnt; i++) dfs3(stk[i]);//处理在同一棵树上的两个节点之间的答案 
    for (int i = 1; i <= cnt; i++) dfs_down(stk[i]);//统计答案 
    for (int i = 1; i <= n; i++)	printf("%lld\n", res[i]);
    return 0;
}