自动搬运

查看原文

来自洛谷，原作者为

	yujinning 初三|7级钩|目标省一

搬运于2025-08-24 22:44:35，当前版本为作者最后更新于2023-02-05 15:18:47，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

前言

一道 USACO-Ag 的题目，T2。

总体难度不大，码量惊人。

解题

首先理解题意。

• 刚开始每个格子都有一个方向标。

• 每次操作修改一个方向标，并实时更新答案。

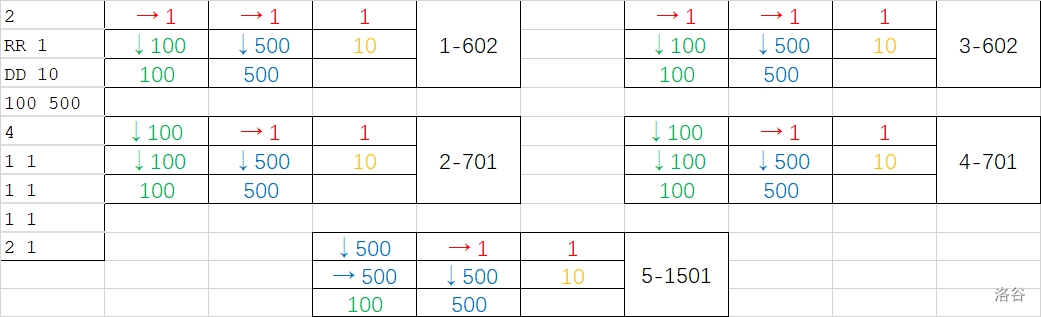
样例答案如下图所示。

解法

可以注意到，对于刚开始的图，每个点所对的饲料桶是确定的。

若将竖列的饲料桶标记为 $1\sim n$，横行的饲料桶标记为 $n+1\sim 2\times n$，则对于每个点，刚开始都有一个确定的饲料桶，可以看成根。

如果把一张图看做成一片森林，则对于样例而言，$(1,1), (1,2)$ 的根为 $1$，$(2,1)$ 的根为 $3$，$(2,2)$ 的根为 $4$。

• 初始计算：对于每个根依次遍历，对于竖列的根第 $n$ 列必须为 $R$，对于横行的根第 $n$ 行必须为 $D$，记录每个点的根，每个根和点的子树大小，每个节点最多遍历一遍，时间复杂度 $O(n^2)$；计算为每个根的子树大小乘对应饲料桶的值。

• 修改计算：对于定点，这个点的子树从原本指向的点的根变为现在指向的点，若原根饲料桶大小为 $i$，现根饲料桶大小为 $j$，上一次操作答案为 $ans$，这个点的子树大小为 $sz$，则操作后答案为 $ans+(j-i)\times sz$，同时遍历子树，修改根。每次操作可以理解为一棵树中的一棵子树被接到了另一棵树里。

• 每次计算实际最多遍历 $2n-1$ 遍，遍历 $Q$ 次，共遍历 $2nQ-Q$ 次。

计算下来，时间复杂度和为 $O(n^2+nQ)$。

代码

本代码内为方便表示点，将点对 $(i,j)$ 表示为数 $(i-1)\times n+j$，可以将所有点表示为 $1-n^2$ 内的数。

另外，给出一组较强的调试数据。

3
RRR 10
DDR 20
RRD 30
40 50 60
4
3 3
1 1
3 3
1 1

输出：

350
200
220
400
350

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll N=1509;
ll n,Q,p[N*2],sz[N*N+2*N],f[N*N+2*N],ans;
char a[N][N];
vector<ll> son[N*N+2*N];
inline ll id(ll x,ll y){
	if(x<=n&&y<=n) return (x-1)*n+y;
	if(x==n+1) return n*n+n+y;
	return n*n+x;
}
inline void dfs(ll x,ll y,ll fa){
	ll ider=id(x,y),iderx=id(x-1,y),idery=id(x,y-1);
	sz[ider]=1;
	f[ider]=fa;
	if(a[x][y-1]=='R'){
		son[ider].push_back(idery);
		dfs(x,y-1,fa);
		sz[ider]+=sz[idery];
	}
	if(a[x-1][y]=='D'){
		son[ider].push_back(iderx);
		dfs(x-1,y,fa);
		sz[ider]+=sz[iderx];
	}
}
inline void dfs_bao(ll x,ll y,ll fa,ll cha){
    ans+=cha;
    f[id(x,y)]=fa;
    if(a[x][y-1]=='R')
		dfs_bao(x,y-1,fa,cha);
	if(a[x-1][y]=='D')
		dfs_bao(x-1,y,fa,cha);
}
int main(){
	ios::sync_with_stdio(false);
	cin.tie(0),cout.tie(0);
	cin>>n;
	for(register ll i=1;i<=n;i++){
		for(register ll j=1;j<=n;j++) cin>>a[i][j];
		cin>>p[i];
	}
	for(register ll i=n+1;i<=2*n;i++) cin>>p[i];
	for(register ll i=1;i<=n;i++){
		if(a[i][n]=='R'){
		    son[n*n+i].push_back(id(i,n));
			dfs(i,n,i);
			sz[n*n+i]=sz[id(i,n)];
		}
	}
	for(register ll i=n+1;i<=2*n;i++){
		if(a[n][i-n]=='D'){
			son[n*n+i].push_back(id(n,i-n));
			dfs(n,i-n,i);
			sz[n*n+i]=sz[id(n,i-n)];
		}
	}
	for(register ll i=1;i<=2*n;i++)
		ans+=p[i]*sz[n*n+i];
	cout<<ans<<endl;
	for(register ll i=1;i<=n;i++){
		f[id(n+1,i)]=i+n;
		f[id(i,n+1)]=i;
	}
	int q=0;
	cin>>Q; q=Q;
	while(Q--){
		ll opx,opy;
		cin>>opx>>opy;
		ll faxyer=0;
		if(a[opx][opy]=='R') faxyer=f[id(opx+1,opy)],a[opx][opy]='D';
		else faxyer=f[id(opx,opy+1)],a[opx][opy]='R';
		ll val=p[faxyer];
		ll cha=val-p[f[id(opx,opy)]];
		dfs_bao(opx,opy,faxyer,cha);
		cout<<ans<<endl;
	}
	return 0;
}