自动搬运

查看原文

来自洛谷，原作者为

	离散小波变换° 有志不在年高，无志空长百岁

搬运于2025-08-24 22:43:20，当前版本为作者最后更新于2022-11-27 08:59:52，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

---

题解

前缀和题。

注意到 $M$ 矩阵可以看作 $B$ 矩阵在行上长度为 $r$ 的循环，在列上长度为 $c$ 的循环，容易想到将原来的 $A$ 矩阵也按照这两个方向上的循环进行染色。使用 $r\times c$ 种颜色染色。

这样子有什么好处呢？我们进行一个特殊的二维前缀和。

$$S_{i,j}=A_{i,j}+S_{i-r,j}+S_{i,j-c}-S_{i-r,j-c}$$

那比如说 $(4,7)$ 位置。$S_{4,7}$ 的值就是 $a_{2,1}+a_{2,4}+a_{2,7}+a_{4,1}+a_{4,4}+a_{4,7}$。换言之，我们对每种颜色都做了一次二维前缀和。

比如，现在需要计算左上角、右下角分别为 $(3,4),(5,7)$ 的子矩阵里，所有绿色元素的和。那么答案就是，

$$S_{5,7}-S_{1,7}-S_{5,1}+S_{1,1}$$

更一般地，如果我们希望计算左上角、右下角分别为 $(x_1,y_1),(x_2,y_2)$ 的子矩阵（$(x_1,y_1)$，$(x_2,y_2)$ 两个位置的颜色相同，设为 $t$）里，所有颜色为 $t$ 的元素之和，答案就是：

$$S_{x_2,y_2}-S_{x_2,y_1-c}-S_{x_1-r,y_2}+S_{x_1-r,y_1-c} $$

现在考察一次询问。

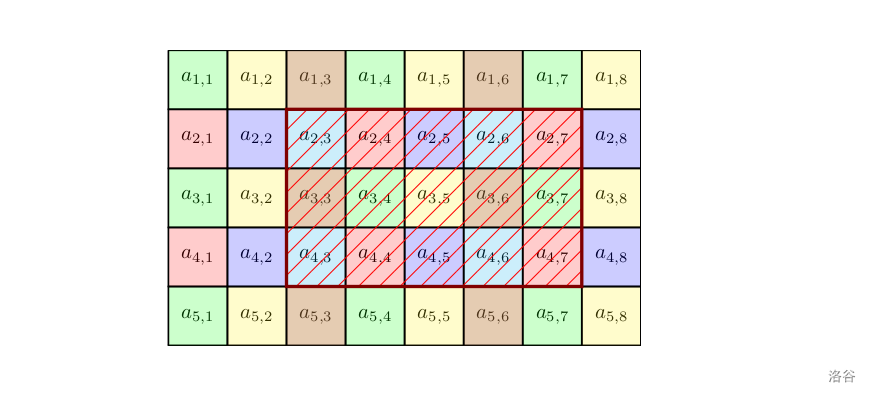
容易发现，我们选取询问矩阵左上角这个 $r\times c$ 的小矩阵，那么这个小矩阵里面应该每种颜色都恰好出现了一次。当然这不是重点，重点是矩阵里所有颜色都会在这个小矩阵出现一次。并且，我们可以根据 $B$ 矩阵算出，哪些颜色对应的 $A_{i,j}$ 值是需要被计算的。

容易计算出小矩阵里的每种颜色，在大矩阵（询问的那个矩阵）里对应的矩阵的左上角、右下角坐标。对于每种颜色，都做一次二维前缀和即可。

时间复杂度为 $\mathcal O(nm+qrc)$。

参考代码

#include<bits/stdc++.h>
#define up(l, r, i) for(int i = l, END##i = r;i <= END##i;++ i)
#define dn(r, l, i) for(int i = r, END##i = l;i >= END##i;-- i)
using namespace std;
typedef long long i64;
const int INF = 2147483647;
int n, m, r, c, q;
int qread(){
    int w=1,c,ret;
    while((c = getchar()) >  '9' || c <  '0') w = (c == '-' ? -1 : 1); ret = c - '0';
    while((c = getchar()) >= '0' && c <= '9') ret = ret * 10 + c - '0';
    return ret * w;
}
const int MAXN = 2e3 + 3;
const int MAXM =  50 + 3;
const int MOD  = 998244353;
int A[MAXN][MAXN], S[MAXN][MAXN]; bool B[MAXN][MAXN];
int calc(int a1, int b1, int a2, int b2){
    int ret = S[a2][b2];
    if(a1 > r) ret = (ret - S[a1 - r][b2] + MOD) % MOD;
    if(b1 > c) ret = (ret - S[a2][b1 - c] + MOD) % MOD;
    if(a1 > r && b1 > c) ret = (ret + S[a1 - r][b1 - c]) % MOD;
    return ret;
}
int main(){
    n = qread(), m = qread();
    up(1, n, i) up(1, m, j) A[i][j] = qread();
    r = qread(), c = qread();
    up(1, r, i) up(1, c, j) B[i][j] = qread();
    up(1, n, i) up(1, m, j){
        S[i][j] = A[i][j];
        if(i > r) S[i][j] = (S[i][j] + S[i - r][j]) % MOD;
        if(j > c) S[i][j] = (S[i][j] + S[i][j - c]) % MOD;
        if(i > r && j > c)
            S[i][j] = (S[i][j] - S[i - r][j - c] + MOD) % MOD;
    }
    q = qread();
    up(1, q, i){
        int _x1 = qread(), _y1 = qread();
        int _x2 = qread(), _y2 = qread();
        int ans = 0;
        up(1, min(r, _x2 - _x1 + 1), a)
            up(1, min(c, _y2 - _y1 + 1), b) if(B[a][b] == 0){
                int a1 = _x1 + a - 1, a2 = a1 + (_x2 - a1) / r * r;
                int b1 = _y1 + b - 1, b2 = b1 + (_y2 - b1) / c * c;
                ans = (ans + calc(a1, b1, a2, b2)) % MOD;
        }
        printf("%d\n", ans);
    }
    
    return 0;
}