自动搬运

查看原文

来自洛谷，原作者为

	rubbishZZZ **

搬运于2025-08-24 22:43:09，当前版本为作者最后更新于2024-03-15 14:54:32，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

提供一个

平面图 Dag 和一个偏序关系是等价的，我们考虑 Dilworth 定理。偏序关系中，最小链覆盖等于最长反链，因此我们想要找最多的没有偏序关系的边。

平面图转对偶图，那么最长反链就是对偶图中从最左边到最右边最长的一个路。题目中给的边是按顺序的，那么我们可以考虑 DP，把平面图中点的信息存在原图中块的右侧的边。

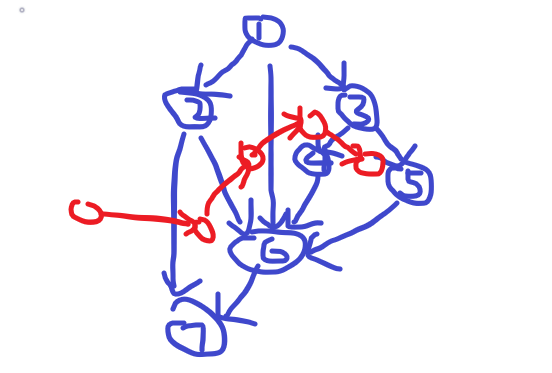
如上图，蓝边为原图的边，红边为对偶图的边，那么红边最长的链砍掉的蓝边就是最长反链，就是答案。

我们设 $f_{x}$ 从最左边到 $x$ 这条边左边的块的最长路，每次不停往上跳，再更新右侧的边的答案。

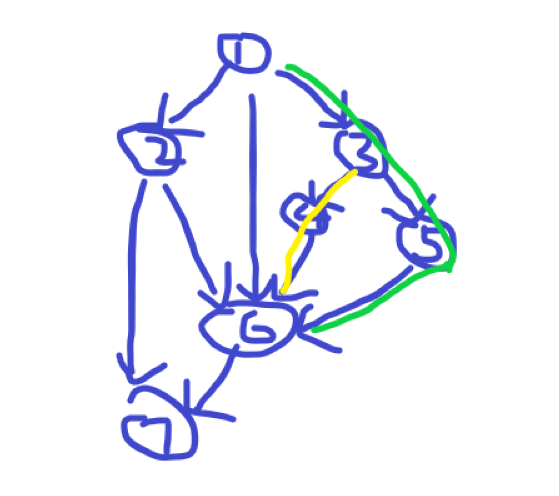
如上图，绿色使我们 dfs 的路径，$6$ 号点访问过了，那我们就用黄色边 $f$ 的最大值来更新 $3$ 到 $5$ 和 $5$ 到 $6$ 两条边的 $f$ 值。

复杂度是 $O(n)$。

代码：

#include <bits/stdc++.h>
#define pii pair<int, int>
#define fi first
#define se second
#define MP make_pair
#define ep emplace
#define eb emplace_back
//#define int long long
#define rep(i, j, k) for (int i = j; i <= k; i++)
#define per(i, j, k) for (int i = j; i >= k; i--)
typedef double db;
typedef long double ldb;
typedef long long ll;
typedef __int128 lll;
typedef unsigned long long ull;
typedef unsigned int ui;
using namespace std;

int read() {
	int s = 0, f = 1;
	char c = getchar();
	while (c < '0' || c > '9') f ^= (c == '-'), c = getchar();
	while (c >= '0' && c <= '9') s = s * 10 + c - '0', c = getchar();
	return f ? s : -s;
}
int n, tot, in[500005], dp[1000005], vis[500005][2], rev[500005], lst[500005], ans;
vector<pii> e[500005];
void dfs(int u) {
	vis[u][0] = 1;
	for (pii p : e[u]) {
		int v = p.fi, id = p.se;
		if (!vis[v][0]) rev[v] = u, lst[v] = id, dfs(v);
		else {
			int Dp = -1, U = u, V = v;
			while (vis[v][1]) Dp = max(Dp, dp[lst[v]]), v = rev[v];
			Dp++;
			ans = max(ans, Dp);
			dp[id] = Dp;
			while (U != v) dp[lst[U]] = Dp, U = rev[U];
			rev[V] = u, lst[V] = id;
		}
	}
	vis[u][1] = 1;
}

signed main() {
	n = read();
	rep(i, 1, n - 1) {
		for (int cnt = read(); cnt--; ) {
			int x = read();
			in[x]++;
			e[i].eb(x, ++tot);
		}
	}
	dfs(1);
	printf("%d\n", ans + 1);
	return 0;
}