自动搬运

查看原文

来自洛谷，原作者为

	Y_ATM_K ด้้้้้็้้้็็็็็้้้้้็็็็็้้้้้้็็็็็้้้้้็็็็็้้้้้้็็็็็้้้้้็็็็็้้้้้้็็็็็้้้้้็็็็็้้้้้้็็AFO!

搬运于2025-08-24 22:41:27，当前版本为作者最后更新于2022-11-22 21:42:41，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

题面传送门

分析

先对灵能传递进行转化。

可以发现，如果把 $a$ 做一遍前缀和得到数组 $s$，那么对于一次对 $i$ 的灵能传递相当于把 $s_i,s_{i-1}$ 交换。

我们令 $s_0 = 0$，剩下的就是把 $s_{1 \sim n-1}$ 重新排列，使得 $\max_{i=1}^{n}{\{|s_i-s_{i-1}|\}}$ 最小。

如果可以移动 $s_0,s_n$，那么直接将 $s$ 排序，这样相邻的差是最小的。

通过上面的思路，不难想到这样的做法：

设 $L = \min(s_0,s_n),R = \max(s_0,s_n)$。先从 $L$ 取到 $s$ 最小值，再取到最大值，最后取到 $R$。

我们对 $s_{1 \sim n-1}$ 排序后，取第一个大于等于 $L$ 的位置 $M$，对于 $1 \sim M-1$ 的数，分别放在 $L,M$ 下面，从大到小地把数放在较小的一边，对 $M+1 \sim n-1$ 的同理。

这样一定是相邻差最小的。

以放 $1 \sim M-1$ 为例。如下图，考虑交换两个数 $x,y$，对于 $x,y$ 上面的 $p,q$，根据前面的贪心策略，一定有 $y \le x \le q \le p$，因此交换后最大距离变大；对于 $x,y$ 下面的 $s,t$ 同理。

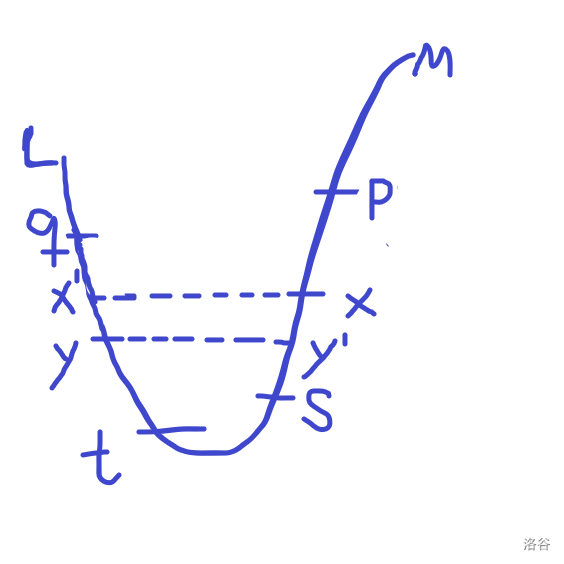
时间复杂度为 $O(Tn \log n)$。

代码

#include <bits/stdc++.h>
#define N 300005
#define ll long long
using namespace std;
int T,n;ll a[N],ans;
int main() {
	scanf("%d",&T);
	while(T--) {
		scanf("%d",&n);
		for(int i=1;i<=n;++i) scanf("%lld",&a[i]),a[i]+=a[i-1];
		sort(a+1,a+n);ans=0;
		ll L=0,R=a[n];if(L>R) swap(L,R);
		int m=lower_bound(a+1,a+n,L)-a;
		ll l=L,r=a[m];
		for(int i=m;i;--i) {
			if(l<r) swap(l,r);
			ans=max(ans,l-a[i]);
			l=a[i];
		}
		ans=max(ans,max(l-r,r-l));
		l=a[m],r=R;
		for(int i=m+1;i<n;++i) {
			if(l>r) swap(l,r);
			ans=max(ans,a[i]-l);
			l=a[i];
		}
		ans=max(ans,max(l-r,r-l));
		if(m==n) ans=max(ans,R-a[n-1]);
		printf("%lld\n",ans);
	}
	return 0;
}