自动搬运

查看原文

来自洛谷，原作者为

	一扶苏一 休息结束。邮箱 yifusuyi@qq.com

搬运于2025-08-24 22:36:52，当前版本为作者最后更新于2022-03-12 20:39:25，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

题外话，比赛时大家好像都在树剖，没见到几个写差分的（（这题不会成了天天爱跑步 2.0 吧（

F2. 生活在树上（hard version）

题意：给定一棵树，点数为 $n$，点有点权。定义树上两点间路径的权值是其简单路径上点权的异或和。有 $q$ 次询问，每次给定两个节点 $x, y$ 查询是否存在一个点 $u$，使 $u$ 到 $x$ 和 $u$ 到 $y$ 的路径的权值的异或为 $k$。

关键词：前缀和，构造，树上差分。

参考难度：绿。

分析：首先异或构成一个 Abel 群，所以如果一个点在 $u$ 到 $x$ 和 $y$ 的路径上都出现了，那么他对答案没有贡献。

考虑 $u$ 到 $x$ 的路径和 $u$ 到 $y$ 的路径总是先经过若干个相同的点，然后与 $(x, y)$ 所成的链有一个交点 $t$，接着在这个交点处分开，一个走向 $x$ 一个走向 $y$，如图：

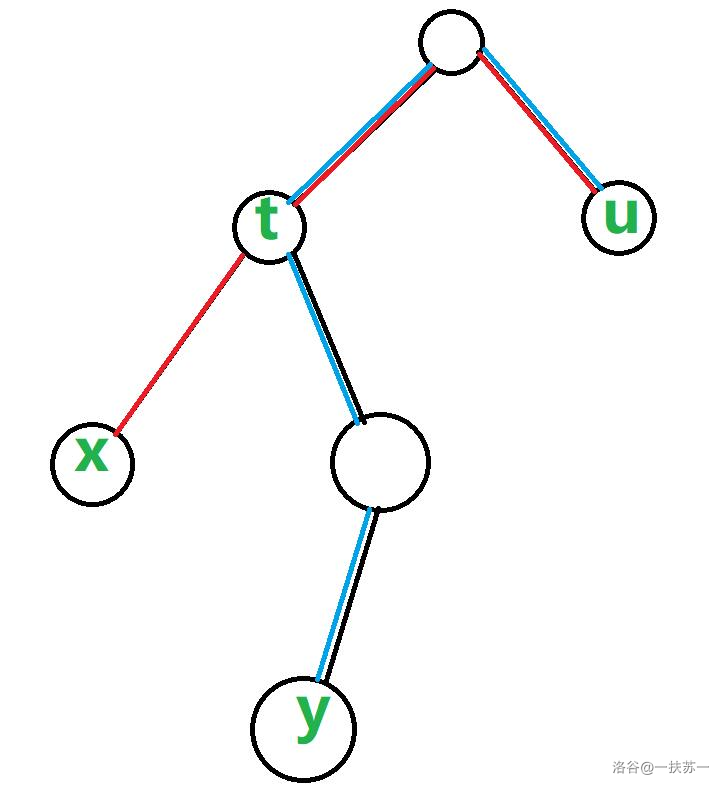
图中红色路径是 $u$ 到 $x$ 的路径，蓝色路径是 $u$ 到 $y$ 的路径，二者在 $(u, t)$ 部分是重复的。不难验证，无论 $u$ 在哪个位置，都满足这个性质。

于是我们发现，$\mathrm{dis}_{u, x} \bigoplus \mathrm{dis}_{u, y}$ 的值可能是 $s_x \bigoplus s_y \bigoplus w_a \bigoplus w_t$，$s_x$ 和 $s_y$ 表示 $x$，$y$ 到根路径的点权异或和，$t$ 是 $x$ 到 $y$ 的链上任何一个点，$a$ 是 $x$ 和 $y$ 的最近公共祖先。注意到 $a$ 在链上，但是 $w_a$ 在 $s_x$ 和 $s_y$ 中都被计算了一次，二者的异或没有了 $w_a$ 的贡献，因此要再异或一次把贡献加回来；此外考虑 $t$ 是两条路径上重复的点，因此对异或和没有贡献，需要异或一次将其贡献去掉。

于是问题就变成了 $s_x \bigoplus s_y \bigoplus w_a \bigoplus w_t = k$ 是否成立。注意到 $x, y, a, k$ 都是定值，根据消去律，$w_t = k \bigoplus s_x \bigoplus s_y \bigoplus w_a$。于是问题转化成了：在 $x$ 到 $y$ 的链上是否存在一个 $t$，使得 $t$ 的权值是 $W= k \bigoplus s_x \bigoplus s_y \bigoplus w_a$。也即查询这条链上权值为 $W$ 的点的个数。这是一个经典的树上差分问题：我们只需要查询 $(x, a)$ 和 $(y, b)$ 两条链上其个数然后相加即可，其中 $b$ 是 $a$ 的「是 $y$ 的祖先的」孩子。我们只需要在 $x, y, a, fa(a)$ 四个点分别打上查询标记，查询这四个位置到根的路径上 $W$ 的权值个数，记为 $p$，则 $(x, y)$ 上 $W$ 权值个数即为 $p_x + p_y - p_a - p_{fa(a)}$。

统计 $p$ 只需要用树上差分的套路，离线询问，在树上打标记，最后进行一次 dfs，用一个全局桶维护当前节点到根的权值数量即可，详见代码。

时间复杂度为 $O(n \log n)$ 或 $O(n \alpha (n))$。其中 $\log n$ 或 $\alpha (n)$ 是求 LCA 的开销。因为本身就需要离线询问，std 使用的是 tarjan 求 LCA 的 $O(n \alpha (n))$ 的做法，使用倍增求 LCA 可能需要一定的常数优化，但是根据验题人程序，也可以通过本题。

(C++)

#include <array>
#include <vector>
#include <iostream>

const int maxn = 1000005;
const int maxw = 10000007;

int n, q;
std::array<std::vector<int>, maxn> e;
std::array<int, maxn> a, b, lca, ufs, rnk, anc, kk, cnt, fa, k, ans;
std::array<bool, maxn> vis;
std::array<std::vector<std::pair<int, int> >, maxn> qry, QQ;
std::array<std::pair<int, int>, maxn> Q;
std::array<int, maxw> bk;

void dfs2(const int u);
void dfs(const int u, const int f);

int main() {
  std::ios::sync_with_stdio(false);
  std::cin.tie(0);
  std::cin >> n >> q;
  for (int i = 1; i <= n; ++i) {
    std::cin >> a[i];
    rnk[ufs[i] = anc[i] = i] = 1;
  }
  for (int u, v, i = 1; i < n; ++i) {
    std::cin >> u >> v;
    e[u].push_back(v); e[v].push_back(u);
  }
  for (int i = 1, u, v; i <= q; ++i) {
    std::cin >> u >> v >> kk[i];
    qry[u].push_back(std::make_pair(v, i));
    qry[v].push_back(std::make_pair(u, i));
    Q[i] = std::make_pair(u, v);
  }
  dfs(1, 0);
  for (int i = 1; i <= q; ++i) if ((k[i] = b[Q[i].first] ^ b[Q[i].second] ^ a[lca[i]] ^ kk[i]) < maxw) {
    QQ[Q[i].first].push_back(std::make_pair(i, 1));
    QQ[Q[i].second].push_back(std::make_pair(i, 1));
    QQ[lca[i]].push_back(std::make_pair(i, -1));
    QQ[fa[lca[i]]].push_back(std::make_pair(i, -1));
  }
  dfs2(1);
  std::array<std::string, 2> prt{"nO\n", "yEs\n"};
  for (int i = 1; i <= q; ++i) std::cout << prt[ans[i] > 0];
}

int find(int x) { return ufs[x] == x ? x : ufs[x] = find(ufs[x]); }

void dfs(const int u, const int f) {
  b[u] = a[u] ^ b[f];
  fa[u] = f;
  for (auto v : e[u]) if (v != f) {
    dfs(v, u);
    int x = find(u), y = find(v);
    if (rnk[x] > rnk[y]) std::swap(x, y);
    anc[ufs[x] = y] = u;
    if (rnk[x] == rnk[y]) ++rnk[y];
  }
  for (auto [v, i] : qry[u]) if (vis[v]) {
    lca[i] = anc[find(v)];
  }
   vis[u] = true;
}

void dfs2(const int u) {	// 这里是树上差分对应求结果的 dfs 函数
  ++bk[a[u]];
  for (auto [i, w] : QQ[u]) {
    ans[i] += w * bk[k[i]];
  }
  for (auto v : e[u]) if (v != fa[u]) {
    dfs2(v);
  }
  --bk[a[u]];
}