自动搬运

查看原文

来自洛谷，原作者为

	ListenSnow True ending

搬运于2025-08-24 22:32:14，当前版本为作者最后更新于2021-09-29 21:26:52，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

题意

有 $N$ 块长方形的木板，长度分别为 $1,2,…,N$，宽度都是 $1$。

现在要用这 $N$ 块木板组成一个宽度为 $N$ 的围栏，满足在围栏中，每块木板两侧的木板要么都比它高，要么都比它低。

也就是说，围栏中的木板是高低交错的。

我们称“两侧比它低的木板”处于高位，“两侧比它高的木板”处于低位。

显然，有很多种构建围栏的方案。

每个方案可以写作一个长度为 $N$ 的序列，序列中的各元素是木板的长度。

把这些序列按照字典序排序，如下图所示，就是 $N=4$ 时，所有满足条件的围栏按照木板长度的字典序排序后的结果。

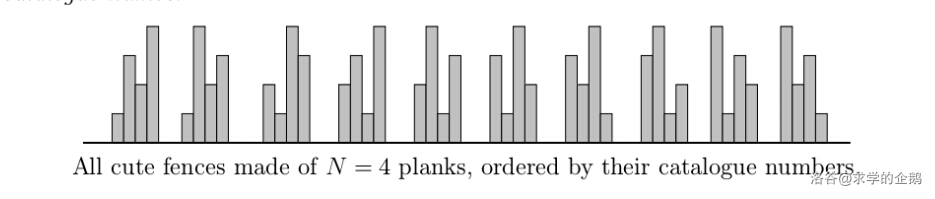
现在给定整数 $C$，求排名为 $C$ 的围栏中，各木板的长度从左到右依次是多少。

数据范围

$1 \leq N \leq 20$，$0 < C <2^{63}$。

思路

思路来源于蓝书。

本题要求字典序排名为 $C$ 的方案，而字典序的排序方式决定了本题可以采用试填法。具体地，第 $i$ 个木板长度从小到大枚举到 $j$ 时，第 $i$ 位，固定填 $j$， $i+1 \sim n$ 的所有填法数量大于等于要求的方案的排名 $m$ ，那么答案中的第 $i$ 位就必然是 $j$。考虑如何预处理出方案数。

定义 $f[n][j][k]$ 表示用 $n$ 块木板组成围栏，最左边的木板在这些木板中排名为 $j$ （题目中隐含了每种长度只能用 $1$ 次的条件），且最左边的木板状态为 $k$ （$k=0$ 表示低位，$k=1$ 表示高位）的所有方案数。可以得到状态转移方程：

$f[i][j][1]=\sum_{k=1}^{j-1} f[i-1][k][0]$。

$f[i][j][0]=\sum_{k=j}^{i-1} f[i-1][k][1]$。

注意到第二个转移方程的 $k \in[j,i-1]$，这是因为 $k$ 代表的是排名，而不是真实的长度，这里其实用到了离散的思想 (如对于 $f[3][1][1]$，$1,3,2$ 和 $4,7,5$ 在状态中都认为是 $1,3,2$，且只会被计算一次)。

接下来就考虑如何试填。由于题目中木板的长度是高低交替，于是可以先确定第一块木板的状态，再用一个数不断异或 $1$ 来表示当前木板需要的状态。后面就可以从小到大枚举，依次确定每一块木板的长度，总复杂度为 $O(N^2)$，预处理的复杂度为 $O(N^3)$。

一些实现细节见代码。

code：

#include<cstdio>
#include<cstring>
using namespace std;
const int N=30;
#define int long long
int f[N][N][2],n,m,T;
bool vis[N];
void init()
{
	f[1][1][1]=f[1][1][0]=1;
	for(int i=2;i<=20;i++)
	    for(int j=1;j<=i;j++)
        {
	        for(int k=1;k<j;k++) f[i][j][1]+=f[i-1][k][0];
	        for(int k=j;k<i;k++) f[i][j][0]+=f[i-1][k][1];
		}
}
signed main()
{
	init();scanf("%lld",&T);
	while(T--)
	{
		scanf("%lld%lld",&n,&m);
		memset(vis,0,sizeof(vis));
		int last,k;
		for(int i=1;i<=n;i++)
		{
			if(f[n][i][1]>=m)//由于是按照字典序，所以优先考虑第二块木板最小的情况 
			{
				last=i,k=1;
				break;
			}
			else m-=f[n][i][1];//由于f[i][j][k] 表示的是方案数，而不是排名，所以需要减去字典序更小的方案数 
			if(f[n][i][0]>=m)
			{
				last=i,k=0;
				break;
			}
			else m-=f[n][i][0];
		}
		printf("%lld",last);vis[last]=true;
		for(int i=2;i<=n;i++)
		{
			k^=1;int rank=0;//rank 表示len在剩余没有选用的木板中排名rank,因为状态中需要用排名 
			for(int len=1;len<=n;len++)
			{
				if(vis[len]) continue;rank++;
				if(k==0&&len<last||k==1&&len>last)
                {
                	if(f[n-i+1][rank][k]>=m)
                	{
                		last=len;
                		break;
					}
					else m-=f[n-i+1][rank][k];
				}
			}
			vis[last]=true;//注意标记当前木板被使用过 
			printf(" %lld",last);
		}
		puts("");
	}
	return 0;
}