自动搬运

查看原文

来自洛谷，原作者为

	aaki code is poetry

搬运于2025-08-24 22:28:33，当前版本为作者最后更新于2021-02-01 16:09:39，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

路线图

我们先拿部分分，然后不断优化收敛，得到满分。

概要分析

当然是把 $\text{[A,Z]}$ 映射为 $[1,26]$。
我们可以把这道题抽象成存在很多山峰，字母映射的数字就是山峰的阶梯高度，我们从西坡登上山顶,然后从东坡下山 。

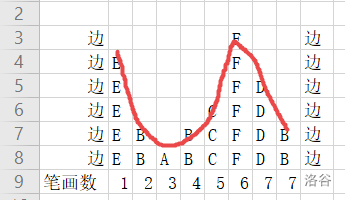
• 对于从西坡上山时，每一级楼梯都是上升的，必然存在山谷,因此需要多画一笔。
• 对于下山时,如果楼梯已经在西坡(也就是上山楼梯)出现过,笔画不增加,如果没出现过,笔画增加。
• 下坡时判断是否是当前山峰的西坡的标准是:向西没有遇到过比当前阶梯更低的山谷。
• 位于左边界的楼梯，我们认为是一步上山的。

拿到49分

分析

对于中间的断层 $[a,b]$ ,我们把数据拆分为 $[1,a-1]$ 和 $[b+1,n]$ 两部分,依次计算画的笔数。

详细设计

• 如果是上升的(就是在西坡上),笔数 + 1 。
• 如果是下降的，使用数组 $v$ 判断当前数字在西坡上是否存在。
• 上坡要新增 $v$ 数据,下坡时要把大于当前高度的数据删除。

代码实现

#include<iostream>
#include<cstring>
using namespace std;
string s;
int ar[100010],n,q,ans,v[30];
int  find(int a,int b){
	memset(v,0,sizeof(v));
	int ans = 0;
	for(int i = a;i<=b;i++){
		if(ar[i] > ar[i-1] || i==a ) ans ++,v[ar[i]] = 1;
		else if(ar[i] < ar[i-1]){
			ans +=(!v[ar[i]]);
			v[ar[i]] = 1;
			for(int j = ar[i] + 1;j<=30;j++) v[j] = 0;
		}
	}
	return ans;
}
void cal(){
	int a,b;
	ans = 0;
	cin >>a>>b;
	if(a>1) ans += find(1,a-1);
	if(b<n) ans += find(b+1,n);
	cout << ans<<endl;
}
int main(){
	cin >> n>>q>>s;
	for(int i = 0;i<n;i++) ar[i+1] = s[i] -'A' +1;
	for(int i  = 1;i<=q;i++)cal();
	return 0;
}

时间复杂度

$O(n \times q)$

当然了循环次数会达到 $10^{10}$ 。

拿到满分

分析

在每次询问现计算是不可能的,我们要想办法把每次询问的时间复杂度降到和 $n$ 无关的 $O(1)$ 。

详细设计

自然,我们想到预处理,因为是分为2段$[1,a-1]$ 和 $[b+1,n]$,因为西段是从1开始的,所以用 $f_i$ 记录在第 $i$ 步时的累计笔数,这是没问题的。 问题出在东段,因为起点是不一定的,西坡情况未知,造成 $f$ 缓存全部失效。

我们知道: 对于相同的一段路径 从西到东走和从东到西走结果是一样的 。 对于东段终点都是 $n$ (也就是从东到西走的起点)是不变的,我们再次从西到东维护一次记录 $fx$ ($fx$ 起点记为 $n$) 。 最终的结果就是：
$f_{a-1} + fx_{b+1}$

代码实现

部分代码

int find2(int a,int b){
	memset(v,0,sizeof(v));
	int ans = 0;
	for(int i = b;i>=a;i--){
		if( ar[i] > ar[i + 1]|| i==b) ans ++,v[ar[i]] = 1;
		else if(ar[i] < ar[i+1]){
			ans +=(!v[ar[i]]);
			v[ar[i]] = 1;
			for(int j = ar[i] + 1;j<=30;j++) v[j] = 0;
		}
		fx[i] = ans;
	}
	return ans;
}
void cal(){
	int a,b;
	ans = 0;
	cin >>a>>b;
	if(a>1) ans += f[a-1];
	if(b<n) ans += fx[b+1];;
	cout << ans<<endl;
}

后记

这道题比赛时是翻车了的,误入了分制算法,想用线段树优化的,把时间白白浪费了。没有想到后缀数组的用法(倒序前缀和) 。

要注意全局变量和局部变量尽量不要重名,否则 debug 时就酸爽了。