自动搬运

查看原文

来自洛谷，原作者为

	hellolin Forever for dreaming!

搬运于2025-08-24 22:24:05，当前版本为作者最后更新于2024-10-10 21:20:01，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

---

注：下文下标统一从 $0$ 开始，根节点是 $0$，区间采用左闭右开记法，一条链包含它的两个端点。

首先我们观察到以下性质：

1. 题目所求 $\sum\limits^{r}_{i=l}f(a,i)$ 可以转为 $\sum\limits^{r}_{i=0}f(a,i)-\sum\limits^{l-1}_{i=0}f(a,i)$，所以修改操作可以只考虑 $[0, r)$ 的情况。
2. 如果对点 $x$ 做修改，答案受影响的节点一定都在 $0\to x$ 的链上。
3. 每个节点的答案一定不小于它的任何一个儿子，也就是说从下至上是单调不降的。
4. 如果我们事先知道某个子树内删除 $x$ 之外的答案，那么我们就可以在 $x$ 更改权值之后知道子树新的答案。

我们先考虑只对于一棵子树，修改一次的情况。根据性质四，我们可以维护子树内最大值和次大值，这样可以快速知道更新后的答案。

再考虑修改多次的情况，我们已经知道了除 $x$ 之外的答案 $v$，值在区间 $[0, r)$ 中取，怎么知道答案之和呢？

如果 $v\geq r-1$，那么无论怎么修改，答案都是 $v$ 不变。修改 $r$ 次的总贡献为 $v\times r$。

如果 $v < r-1$，那么前 $v$ 次修改时答案都是 $v$，后面 $r-v$ 次答案为 $v,v+1,v+2,\dots,r-1$。修改 $r$ 次的总贡献为：

$$\begin{aligned} &v^2+v+(v+1)+(v+2)+\dots+(r-1)\\ =\ &v^2+\frac{(r+v-1)(r-v)}{2}\\ =\ &v^2+\frac{r^2-v^2-r+v}{2}\\ =\ &\frac{v^2+v}{2}+\frac{r^2-r}{2} \end{aligned} $$

最后我们考虑影响多棵子树怎么做。还是设修改 $x$ 节点，值在区间 $[0, r)$ 取。

根据性质二、性质三，最大值（和次大值）自下而上单调不降，也就是在某一个节点之前，删除 $x$ 之外的答案是子树次大值，在之后是子树最大值。这个分界点我们倍增找就行了。

不难发现这个分界点以下以及以上的区间，又分成了 $v < r-1$ 和 $v \geq r-1$ 的区间，一共四个小区间。我们还是倍增找到这两个分界点。

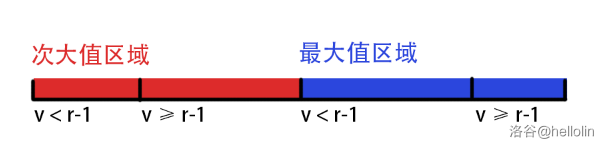
对于 $v\geq r-1$ 的区间，它们都是链上连续的一段，对于次大值与最大值记录 $v\times r$ 前缀和即可。

对于 $v<r-1$ 的区间，总贡献为（$\mathrm{len}$ 为区间长度）：

$$\begin{aligned} &\sum(\frac{v^2+v}{2}+\frac{r^2-r}{2})\\ =\ &\frac{\sum v^2+\sum v}{2}+\frac{\mathrm{len}\times (r^2-r)}{2} \end{aligned} $$

维护一下子树内答案和、答案平方和，树剖查询即可。

树剖和倍增初始化 $O(n\log n)$，查询 $O(\log n)$，前缀和初始化 $O(n)$，查询 $O(1)$。总时间复杂度 $O(n\log n)$，写得优秀一点是可以跑进 2s 的。

#include "hellolin/common.hpp"
#include "hellolin/utils.hpp"
#include "hellolin/io.hpp"

namespace hellolin {
static constexpr i64 Mod = 998244353, Inv2 = 499122177;

struct SubTree {
  i64 fir = 0, sec = 0;
  friend SubTree operator+(const auto &l, const auto &r) {
    if (l.fir == r.fir) {
      return {l.fir, r.fir};
    } else if (l.fir > r.fir) {
      return {l.fir, max(l.sec, r.fir)};
    } else {
      return {r.fir, max(r.sec, l.fir)};
    }
  }
  SubTree &operator+=(const auto &r) {
    return *this = *this + r;
  }
};

struct Node {
  struct {
    i64 sum = 0, squ = 0;
  } fir, sec;
  Node operator-() const {
    return { {-fir.sum, -fir.squ}, {-sec.sum, -sec.squ} };
  }
  friend Node operator+(const auto &l, const auto &r) {
    return { {l.fir.sum + r.fir.sum, l.fir.squ + r.fir.squ}, {l.sec.sum + r.sec.sum, l.sec.squ + r.sec.squ} };
  }
  friend Node operator-(const auto &l, const auto &r) {
    return l + -r;
  }
  Node &operator+=(const auto &r) {
    return *this = *this + r;
  }
  Node &operator-=(const auto &r) {
    return *this = *this - r;
  }
};

void main() {
  int n, q, opt;
  io.read(n, q, opt);

  std::vector<int> val(n);
  io.read(val);

  std::vector<std::vector<int>> g(n);
  for (int i = 1, u, v; i < n; ++i) {
    io.read(u, v);
    --u, --v;
    g[u].push_back(v);
    g[v].push_back(u);
  }

  std::vector<int> son(n, -1), dfn(n), idx(n), siz(n), dep(n), top(n);
  std::vector<std::vector<int>> anc(20, std::vector<int> (n));
  std::vector<SubTree> tree(n);
  std::vector<Node> presum(n);
  int tot = 0;

  auto dfs1 = [&](auto &&f, int x, int fa) -> void {
    siz[x] = 1;
    dep[x] = (fa == -1 ? -1 : dep[fa]) + 1;
    anc[0][x] = fa;
    tree[x] = {val[x], 0};

    for (const int &y : g[x]) {
      if (y == fa) continue;
      f(f, y, x);
      siz[x] += siz[y];
      if (son[x] == -1 or siz[y] > siz[son[x]]) son[x] = y;
      tree[x] += tree[y];
    }
  };
  auto dfs2 = [&](auto &&f, int x, int tp) -> void {
    idx[dfn[x] = tot++] = x;
    top[x] = tp;
    if (son[x] != -1) f(f, son[x], tp);
    for (const int &y : g[x]) {
      if (y == anc[0][x] or y == son[x]) continue;
      f(f, y, y);
    }
  };
  dfs1(dfs1, 0, -1);
  dfs2(dfs2, 0, 0);
  for (int i = 1; i <= 19; ++i) {
    anc[i][0] = -1;
    for (int j = 1; j < n; ++j) {
      if (anc[i - 1][j] != -1)
        anc[i][j] = anc[i - 1][anc[i - 1][j]];
      else
        anc[i][j] = -1;
    }
  }

  presum[0] = {
      {tree[0].fir, tree[0].fir * tree[0].fir},
      {tree[0].sec, tree[0].sec * tree[0].sec}
  };
  for (int i = 1; i < n; ++i) {
    int cur = idx[i];
    presum[i] = presum[i - 1] + Node({
      {tree[cur].fir, tree[cur].fir * tree[cur].fir},
      {tree[cur].sec, tree[cur].sec * tree[cur].sec}
    });
  }

  auto query = [&](int l, int r) {
    if (l == 0) return presum[r - 1];
    return presum[r - 1] - presum[l - 1];
  };

  auto queryLink = [&](int x, int y) {
    Node result;
    while (top[x] != top[y]) {
      if (dep[top[x]] < dep[top[y]]) swap(x, y);
      result += query(dfn[top[x]], dfn[x] + 1);
      x = anc[0][top[x]];
    }
    if (dep[x] > dep[y]) swap(x, y);
    result += query(dfn[x], dfn[y] + 1);
    return result;
  };

  auto solve = [&](int a, i64 r) -> i64 {
    if (r <= 0) return 0;
    i64 result = 0;

    int b = a;
    for (int i = 19; i >= 0; --i) {
      if (anc[i][b] == -1) continue;
      if (tree[anc[i][b]].fir <= val[a]) b = anc[i][b];
    }

    if (tree[b].fir <= val[a]) {
      int c = a;
      for (int i = 19; i >= 0; --i) {
        if (anc[i][c] == -1 or dep[b] > dep[anc[i][c]]) continue;
        if (tree[anc[i][c]].sec < r - 1) c = anc[i][c];
      }

      if (tree[c].sec < r - 1) {
        Node link = queryLink(a, c);
        i64 count = dep[a] - dep[c] + 1;
        i64 delta = (count * (r * (r - 1) % Mod) % Mod + link.sec.squ + link.sec.sum) % Mod * Inv2 % Mod;
        result = (result + delta % Mod) % Mod;
        c = anc[0][c];
      }
      if (c != -1 and dep[c] >= dep[b]) {
        Node link = queryLink(c, b);
        result = (result + link.sec.sum * r % Mod) % Mod;
      }
      b = anc[0][b];
    }
    if (b == -1) return result;

    int d = b;
    for (int i = 19; i >= 0; --i) {
      if (anc[i][d] == -1) continue;
      if (tree[anc[i][d]].fir < r - 1) d = anc[i][d];
    }

    if (tree[d].fir < r - 1) {
      Node link = queryLink(b, d);
      i64 count = dep[b] - dep[d] + 1;
      i64 delta = (count * (r * (r - 1) % Mod) % Mod + link.fir.squ + link.fir.sum) % Mod * Inv2 % Mod;
      result = (result + delta % Mod) % Mod;
      d = anc[0][d];
    }
    if (d != -1) {
      Node link = queryLink(d, 0);
      result = (result + link.fir.sum * r % Mod) % Mod;
    }

    return result;
  };

  i64 answer = 0, origin = query(0, n).fir.sum;
  for (int i = 0, l, r, a; i < q; ++i) {
    io.read(l, r, a);
    l = (answer * opt + (i64) l) % n + 1;
    r = (answer * opt + (i64) r) % n + 1;
    a = (answer * opt + (i64) a) % n + 1;
    if (l > r) swap(l, r);
    ++r, --a;

    Node link = queryLink(a, 0);
    answer = ((origin - link.fir.sum) * (r - l) % Mod + solve(a, r) - solve(a, l)) % Mod;
    answer = (answer + Mod) % Mod;
    io.writeln(answer);
  }
}
} // namespace hellolin

int main() { hellolin::main(); }