自动搬运

查看原文

来自洛谷，原作者为

	liuliucy **

搬运于2025-08-24 22:23:39，当前版本为作者最后更新于2023-08-02 15:58:20，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

---

各种情况

首先，我们可以用边权表示出每个点的点权：

$$2a_i=\sum_j e_{i,j}$$

$e_{i,j}$ 表示一条从 $i$ 到 $j$ 的边的边权。然后，我们便可以列出一个方程组：

$$\left\{\begin{matrix} \sum_j e_{1,j}=2a_1\\ \sum_j e_{2,j}=2a_2\\... \\ \sum_j e_{n,j}=2a_n \end{matrix}\right.$$

有 $n$ 个方程，$m$ 个未知数，我们用高斯消元暴力我们可以知道当 $m>n$ 时方程组有无数组解，图是联通的，所以只可能 $m=n-1$ 或者 $m=n$ ，当 $m=n-1$，这是一棵树，而 $m=n$ 时则是基环树。

我们分别考虑以下三种情况：

如图所示时：

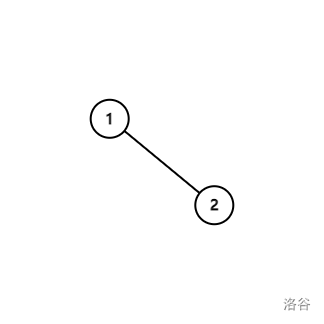
这显然是可以直接算的，因为 $a_1$ 点权的两倍就是 $1-2$ 的边权。

当是个环时：

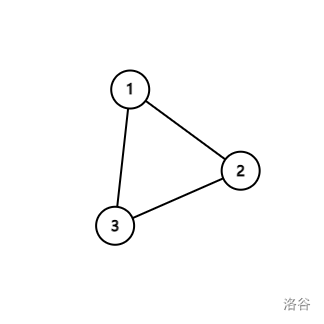
我们可以列出方程组：

$$\left\{\begin{matrix} e_{1,2}+e_{1,3}=2a_1\\ e_{2,3}+e_{1,2}=2a_2\\ e_{1,3}+e_{2,3}=2a_3 \end{matrix}\right.$$

我们将 $1$ 式减去 $2$ 式 加上 $3$ 式便可得到 $2e_{1,3}$ 的值，之后便可得到所有的边权。

而当环上有偶数个点时：

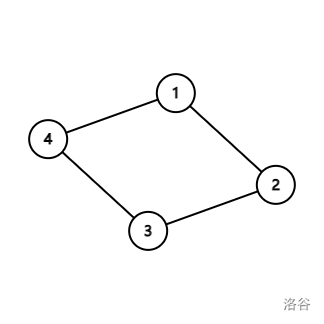
这也有无穷多组解，因为我们将 $e_{1,4}$ 加 $1$ ，$e_{1,2}$ 减 $1$，之后再将 $e_{2,3}$ 加 $1$，$e_{3,4}$ 减 $1$，我们发现这样也是成立的，但是却得到了不同的一组解，所以这样会出现无穷多组解。

算法

我们先拓扑排序，先处理掉链的情况，最后只剩下环，最后再处理环即可。

CODE

#include<bits/stdc++.h>
using namespace std;
struct xx{
	int x,id,nxt;
}e[1000001];
int head[1000001],cnt;
bool b[1000001];
void add(int x,int y,int id){
	e[++cnt].x=y;
	e[cnt].id=id;
	e[cnt].nxt=head[x];
	head[x]=cnt;
}
bool vis[1000001];
bool used[1000001];
int a[1000001],in[10000001];
int ans[10000001];
queue<int>q;
int n,m,aw,ct,f=1;
void dfs1(int x,int fa,int rt){
	if(fa!=-1&&rt==x){
		if(ct%2==0){
			printf("0");
			exit(0);
		}
		return;
	}
	aw+=f*a[x];
	f*=-1;
	ct++;
	for(int i=head[x];i!=-1;i=e[i].nxt){
		int y=e[i].x;
		if(y==fa)continue;
		if(in[y]<2)continue;
		if(b[y])continue;
		b[y]=1;
		dfs1(y,x,rt);
	}
}
void dfs2(int x,int fa,int rt){
	if(fa!=-1&&rt==x)return;
	for(int i=head[x];i!=-1;i=e[i].nxt){
		int y=e[i].x;
		if(y==fa)continue;
		if(in[y]<2)continue;
		if(b[y])continue;
		b[y]=1;
		aw=a[x]-aw;
		ans[e[i].id]=2*aw;
		dfs2(y,x,rt);
		
	}
}
signed main(){
	memset(head,0xff,sizeof(head));
	scanf("%d%d",&n,&m);
	if(m>n){
		putchar('0');
		return 0;
	}
	for(int i=1;i<=n;i++)scanf("%d",&a[i]);
	for(int i=1;i<=m;i++){
		int x,y;
		scanf("%d%d",&x,&y);
		add(x,y,i);
		add(y,x,i);
		in[y]++;in[x]++;
	}
	for(int i=1;i<=n;i++)if(in[i]==1)q.push(i);
	while(!q.empty()){
		int x=q.front();
		q.pop();
		if(used[x])continue;
		used[x]=1;
		for(int i=head[x];i!=-1;i=e[i].nxt){
			int y=e[i].x,id=e[i].id;
			if(vis[id])continue;
			ans[id]=2*a[x];
			a[y]-=a[x];
			vis[id]=1;
			in[y]--;
			if(in[y]==1){
				q.push(y);
			}
		}
	}
	memset(b,0,sizeof(b));
	for(int i=1;i<=n;i++){
		if(b[i])continue;
		if(in[i]>=2){
			dfs1(i,-1,i);
			memset(b,0,sizeof(b));
			aw/=2;
			dfs2(i,-1,i);
		}
	}
	for(int i=1;i<=cnt/2;i++)printf("%d\n",ans[i]);
}