自动搬运

查看原文

来自洛谷，原作者为

	Karry5307 兄弟会背叛你，女人会离开你，金钱会诱惑你，生活会刁难你，只有数学不会，不会就是不会，怎么学都不会

搬运于2025-08-24 22:23:37，当前版本为作者最后更新于2020-08-08 18:28:56，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

题意

略。

前言

作为验题人，被出题人甩了锅来写标程，在写标程的时候发现这题是真的难写。

所以在讲这个题的时候不仅有出题人的一些方法，也有自己的体会。

某些图是蒯的神仙 JV 的。

题解

首先将 $2n\times 2m$ 的方格划分成 $n\times m$ 个 $2\times 2$ 的小方格，注意到由于限制条件，每个 $2\times 2$ 方格里只能摆上一个攻城锤，然后整个图的摆法必须像这样：

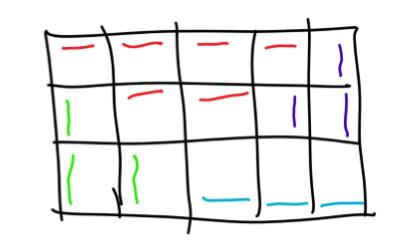
接下来规定一个 $2\times 2$ 的方格的上下左右，就是这个方格内攻城锤的相对位置。

接下来考虑算这个摆法的方案数。考虑划两条分界线，一条分割上右和下左，另一条是上左和下右，如下图：

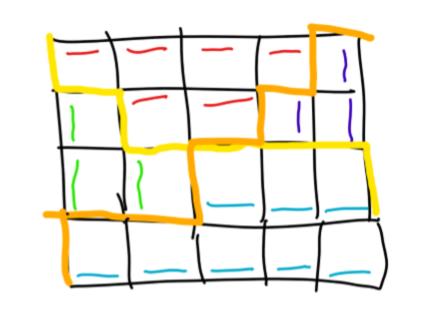
相当于我们只需要算出两条分界线的划法，将这两条分界线的方案数乘起来就可以得到总数。

接下来考虑划分上右和下左的方案数，另一条分界线如法炮制一遍就可以了。

这个分界线其实也可以理解为从左上角走到右下角的方案数，注意到有一些点因为钦定放的位置的限制是不能走的。左和下所在 $2\times 2$ 方格的左下角，右和上所在 $2\times 2$ 方格的右上角都是不能走到的。

接下来注意到 $m$ 很大，因此要一列一列来考虑。我们首先将可以走的点划分成一些矩形，然后考虑使用生成函数。

在矩形的内部，下一列方案数所对应的生成函数就是这一行的生成函数乘上 $\frac{1}{1-x}$。而在矩形的边界处就不一定了。

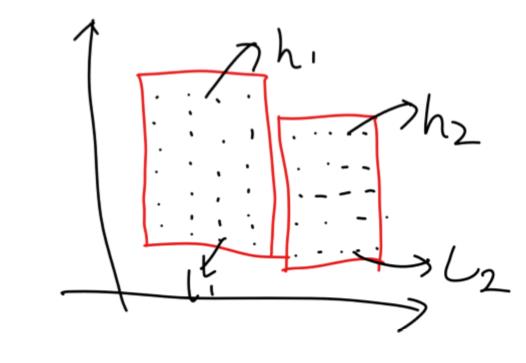
在这种情况下，对于左边的矩形的右边界转移到右边矩形的左边界的时候，先将 $h_1\sim h_2-1$ 次项的系数清零，然后做一遍前缀和，再将 $l_1+1\sim l_2$ 次项的系数全部用 $l_1$ 次项的系数填充就好了。

这样，由于矩形最多有 $n$ 个，然后每一次操作是 $O(n)$ 的，所以总时间复杂度为 $O(n^2)$。

大体操作就讲到这里，接下来是代码细节。

首先一个需要注意的点就是到底哪些点是不能走的。还是以左下和右上的分界线为例子，注意到左下的限制和右上的限制其实是一个凸包，所以可以排个序然后单调栈维护一下。

接下来最麻烦的是矩形划分，这里可以考虑使用归并排序的思想。对于每个矩形，我们记录他的左右端点和上下边界。然后对于每个凸包上的点都会造成矩形的边界更新。

然后分 $3$ 种情况下一个左端点和下一个右端点的位置关系。这里有个小细节，就是对于每个上边界的改变来说位置的更新应该是对应的 $y$ 坐标减 $1$。

最后就是维护这个多项式，我们可以不用记录实际的多项式而是记录这个多项式乘上 $(1-x)^t$，然后剩下的就随便做就好了。

代码

#include<bits/stdc++.h>
using namespace std;
typedef int ll;
typedef unsigned int ul;
typedef long long int li;
typedef unsigned long long int ull;
const ll MAXN=2e5+51;
struct Point{
	li x1,y1,x2,y2;
	ll dir;
};
struct Point2{
	li x,y;
	inline bool operator <(const Point2 &rhs)const
	{
		return x<rhs.x;
	}
	inline bool operator >(const Point2 &rhs)const
	{
		return x>rhs.x;
	}
};
struct Event{
	li y,lx,rx,lp,rp;
};
struct Rect{
	li u,d,ly,ry;
};
inline ll getR(ll MOD)
{
	ul v=MOD;
	return v*=2-MOD*v,v*=2-MOD*v,v*=2-MOD*v,v*=2-MOD*v,v;
}
Point pt[MAXN];
Point2 pt2l[MAXN],pt2r[MAXN],pt3l[MAXN],pt3r[MAXN];
Event ev[MAXN];
Rect rect[MAXN];
ll n,kk,MOD,R,R2;
li m,x,y,xt,yt;
inline ul reduce(ull x)
{
	ull y=ul(x>>32)-ul((ull(ul(x)*R)*MOD)>>32);
	return y+(MOD&-((ll)y<0));
}
struct ModInt{
	ul v;
	ModInt()
	{
		v=0;
	}
	ModInt(ul v)
	{
		this->v=reduce(ull(v)*R2);
	}
	ModInt(const ModInt &rhs)
	{
		this->v=rhs.v;
	}
	inline ModInt operator -()
	{
		ModInt res;
		res.v=(MOD&-(v!=0))-v;
		return res;
	}
	inline ModInt &operator +=(const ModInt &rhs)
	{
		return v+=rhs.v-MOD,v+=MOD&-(ll(v)<0),*this;
	}
	inline ModInt &operator -=(const ModInt &rhs)
	{
		return v-=rhs.v,v+=MOD&-(ll(v)<0),*this;
	}
	inline ModInt &operator *=(const ModInt &rhs)
	{
		return v=reduce(ull(v)*rhs.v),*this;
	}
	inline ll get()
	{
		return reduce(v);
	}
};
inline ModInt operator +(const ModInt &x,const ModInt &y)
{
	return ModInt(x)+=y;
}
inline ModInt operator -(const ModInt &x,const ModInt &y)
{
	return ModInt(x)-=y;
}
inline ModInt operator *(const ModInt &x,const ModInt &y)
{
	return ModInt(x)*=y;
}
ModInt r1,r2;
ModInt f[MAXN],inv[MAXN];
inline li read()
{
    register li num=0,neg=1;
    register char ch=getchar();
    while(!isdigit(ch)&&ch!='-')
    {
        ch=getchar();
    }
    if(ch=='-')
    {
        neg=-1;
        ch=getchar();
    }
    while(isdigit(ch))
    {
        num=(num<<3)+(num<<1)+(ch-'0');
        ch=getchar();
    }
    return num*neg;
}
inline ModInt get(ModInt *f,ll x,li kk)
{
	ModInt res(0);
	static ModInt p[MAXN];
	for(register int i=0;i<=x;i++)
	{
		p[i]=0;
	}
	p[0]=1,p[1]=(kk%=MOD);
	for(register int i=2;i<=x;i++)
	{
		p[i]=p[i-1]*(ModInt)(kk-1+i)*inv[i];
	}
	for(register int i=0;i<=x;i++)
	{
		res+=f[i]*p[x-i];
	}
	return res;
}
inline void change(ModInt *f,ll x,li kk,ModInt val)
{
	ModInt v=val-get(f,x,kk);
	ll sz=min((li)n,kk);
	static ModInt p[MAXN];
	for(register int i=0;i<=n;i++)
	{
		p[i]=0;
	}
	p[0]=1,kk%=MOD;
	for(register int i=1;i<=sz;i++)
	{
		p[i]=p[i-1]*ModInt(kk-i+1+MOD)*inv[i];
	}
	for(register int i=0;i<=sz;i++)
	{
		p[i]=i&1?p[i]:p[i];
	}
	for(register int i=0;i<=n;i++)
	{
		if(i+x<=n)
		{
			f[i+x]=f[i+x]+v*p[i];
			continue;
		}
		break;
	}
}
inline void clr(ModInt *f,ll x,li kk)
{
	static ModInt p[MAXN],q[MAXN],r[MAXN];
	ll sz=min((li)n,kk);
	for(register int i=0;i<=n;i++)
	{
		p[i]=q[i]=r[i]=0;
	}
	for(register int i=0;i<=sz;i++)
	{
		p[i]=get(f,i,kk);
	}
	q[0]=1,kk%=MOD;
	for(register int i=1;i<=sz;i++)
	{
		q[i]=q[i-1]*ModInt(kk-i+1)*inv[i];
	}
	for(register int i=0;i<=sz;i++)
	{
		q[i]=i&1?-q[i]:q[i];
	}
	for(register int i=0;i<=x;i++)
	{
		for(register int j=0;j<=sz;j++)
		{
			if(i+j<=n)
			{
				r[i+j]+=p[i]*q[j];
                continue;
			}
            break;
		}
	}
	for(register int i=0;i<=n;i++)
	{
		f[i]=f[i]-r[i];
	}
} 
inline void solve()
{
	ll lt=0,rt=0,lt3=0,rt3=0,lct=1,rct=1,rtx=1,u=0,d=0;
	ModInt val=0;
	for(register int i=1;i<=kk;i++)
	{
		if(pt[i].dir==1||pt[i].dir==2)
		{
			pt2l[++lt]=(Point2){(pt[i].x2+1)/2,(pt[i].y2+1)/2-1};
		}
		else
		{
			pt2r[++rt]=(Point2){(pt[i].x2+1)/2-1,(pt[i].y2+1)/2};
		}
	}
	sort(pt2l+1,pt2l+lt+1),sort(pt2r+1,pt2r+rt+1,greater<Point2>());
	pt3l[0].x=0,pt3l[0].y=-1,pt3r[0].x=0,pt3r[0].y=0x3f3f3f3f3f3f3f3f;
	for(register int i=1;i<=lt;i++)
	{
		if(pt2l[i].y>pt3l[lt3].y)
		{
			pt3l[++lt3]=pt2l[i];
		}
	}
	for(register int i=1;i<=rt;i++)
	{
		if(pt2r[i].y<pt3r[rt3].y)
		{
			pt3r[++rt3]=pt2r[i];
		}
	}
	for(register int i=1;i<=rt3;i++)
	{
		pt3r[i].y--;
	}
	reverse(pt3r+1,pt3r+rt3+1),u=0,d=lt3?pt3l[1].x-1:n;
	for(register int i=0;i<=d;i++)
	{
		f[i]=ModInt(1);
	}
	rect[1].u=u,rect[1].d=d,rect[1].ly=0;
	while(1)
	{
		if(lct>lt3||rct>rt3)
		{
			break;
		}
		if(pt3l[lct].y<pt3r[rct].y)
		{
			rect[rtx].ry=pt3l[lct].y,d=lct<lt3?pt3l[lct+1].x-1:n;
			rect[++rtx].u=u,rect[rtx].d=d,rect[rtx].ly=pt3l[lct++].y+1;
		}
		if(pt3l[lct].y>pt3r[rct].y)
		{
			rect[rtx].ry=pt3r[rct].y,u=pt3r[rct].x+1;
			rect[++rtx].u=u,rect[rtx].d=d,rect[rtx].ly=pt3r[rct++].y+1;
		}
		if(pt3l[lct].y==pt3r[rct].y)
		{
			rect[rtx].ry=pt3l[lct].y,u=pt3r[rct].x+1;
			d=lct<lt3?pt3l[lct+1].x-1:n;
			rect[++rtx].u=u,rect[rtx].d=d,rect[rtx].ly=pt3l[lct++].y+1,rct++;
		}
	}
	for(register int i=lct;i<=lt3;i++)
	{
		rect[rtx].ry=pt3l[i].y,rect[++rtx].u=u;
		rect[rtx].d=i<lt3?pt3l[i+1].x-1:n,rect[rtx].ly=pt3l[i].y+1;
	}
	for(register int i=rct;i<=rt3;i++)
	{
		rect[rtx].ry=pt3r[i].y,rect[++rtx].u=pt3r[i].x+1,rect[rtx].d=d;
		rect[rtx].ly=pt3r[i].y+1;
	}
	rect[rtx].ry=m;
	for(register int i=2;i<=rtx;i++)
	{
		clr(f,rect[i].u-1,rect[i-1].ry);
        val=get(f,rect[i-1].d,rect[i].ly);
		for(register int j=rect[i-1].d+1;j<=rect[i].d;j++)
		{
			change(f,j,rect[i].ly,val);
		}
	}
}
int main()
{
	n=read(),m=read(),kk=read(),MOD=read();
	R=getR(MOD),R2=-ull(MOD)%MOD;
	for(register int i=1;i<=kk;i++)
	{
		x=read(),y=read(),xt=read(),yt=read();
		if(x==xt&&y>yt)
		{
			swap(y,yt);
		}
		if(y==yt&&x>xt)
		{
			swap(x,xt);
		}
		pt[i]=(Point){x,y,xt,yt};
		if(y==yt&&x+1==xt)
		{
			pt[i].dir=1+2*((yt&1)^1);
		}
		if(x==xt&&y+1==yt)
		{
			pt[i].dir=2+2*(xt&1);
		}
	}
	inv[1]=ModInt(1);
	for(register int i=2;i<=n;i++)
	{
		inv[i]=-ModInt(MOD/i)*inv[MOD%i];
	}
	solve(),r1=get(f,n,m);
	for(register int i=1;i<=kk;i++)
	{
		pt[i].y1=2*m-pt[i].y1+1,pt[i].y2=2*m-pt[i].y2+1;
		if(pt[i].dir&1)
		{
			pt[i].dir^=2;
		}
		else
		{
			swap(pt[i].y1,pt[i].y2);
		} 
	}
	solve(),r2=get(f,n,m),printf("%d\n",(r1*r2).get());
}