自动搬运

查看原文

来自洛谷，原作者为

	yangrunze 蓝蓝的天空银河里，有只小白船

搬运于2025-08-24 22:22:19，当前版本为作者最后更新于2020-06-07 17:24:03，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

---

蒟蒻作为出题人$\colorbox{black}{\color{black}的好基友}$，特地$\colorbox{black}{\color{black}好不容易弄懂了}$来写一发$\colorbox{black}{\color{black}非}$官方题解！

$$\huge\color{purple}{\text {vectorwyx}}\;\color{gold}\text{是我们的王}\;\color{red}\text! $$

---

据比赛官方透露，这个题是经过加强的

在加强之前，字母T是没有限制的（即$a=b=s=x=0$）

所以咱们就从这种情况入手，这样有利于向正解进发！

分析一下字母T的组成吧……

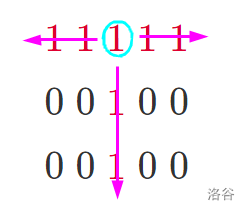
可以发现：对于图中的每一个含 $1$ 的点，字母T的数量跟它左，右，下三个方向上连续的 $1$ 的个数有关。

设这个点左，右，下三个方向连续$1$的个数为$l,r,d$，则以这个点为中心点的字母T的数量为$(\min(l,r)-1)\times(d-1)$

所以我们可以先把每个点的$l,r,d$处理出来，这样就可以解决问题啦！

但是怎么处理呢，一个个找？

不，我们用前缀和。

直接上代码吧！（话说$r$和$d$实际上是后缀和呢）

	bool wyx[3005][3005];//题目给的01矩阵（wyx是我们的红太阳！！！）
	long long sl[3005][3005],sr[3005][3005],sd[3005][3005];//l,r,d（开 long long 啊awa）
	//如果这里是1，那就加上前面的
	for(int i=1;i<=n;i++){
		for(int j=1;j<=m;j++)
		if(wyx[i][j])sl[i][j]=sl[i][j-1]+1;
	}
	//后面的亦如此，但是要注意一下循环顺序    
	for(int i=1;i<=n;i++){
		for(int j=m;j>0;j--)
		if(wyx[i][j])sr[i][j]=sr[i][j+1]+1;
	}
	for(int i=n;i>0;i--){
		for(int j=1;j<=m;j++)
		if(wyx[i][j])sd[i][j]=sd[i+1][j]+1;
	}	

这样的话，我们就完美迈出了AC的第一步！

---

接下来，咱们来考虑$w$和$h$的限制条件：

对于每个 $w$，我们可以算出最小的合法 $h$。 ——君のNOIP。

那怎么算呢？我们来看看这四个条件：

$$\begin{cases}h\ge b\quad (\text{限制条件2})\\h\ge \lceil\dfrac{s}{w}\rceil\quad (\text{限制条件3})\\h\ge x-w\quad (\text{限制条件4})\end{cases} $$

因为都要满足，所以我们从三个值里面要取个最大的，即：

	long long minh[3005];//minh:对于每个w，它的最大合法h		
	for(int w=a+!(a&1);w<=m;w+=2)//因为w>=a，所以只需要从a开始，加!(a&1)是为了保证w为奇数

这样的话，对于任意情况我们都可以通过枚举中心点和$w$ 的方式在$O(n^3)$的时间内算出来啦！

但是……这貌似还不太够……

---

接下来就是最后一战了：我们要把$O(n^3)$优化成$O(n^2)$

$\color{red}{\text{敲黑板！！！重难点来啦！！！！！}}$

往深入里思考一下，我们需要把$w$和$h$的范围确定下来。

不难看出：$b\le h\le d$

然后再来考虑 $w$，$w$ 的最大值是$2\times\min(l,r)-1$……

但是 $w$ 的最小值是啥？？？？？

别急嘛，既然前面我们已经推出了对于每个 $w$ 最小的合法 $h$，那我们也可以推出对于每一个 $h$ 的最小合法 $w$ ！

既然我们已经推出了$\min h$，那我们可以好好利用一下：要求出某个 $h$ 的 $\min w$值，就是寻找一个 $w$，使这个 $w$ 的 $\min h\le h$

	int w=a+!(a&1);//w还是从a开始
	for(int h=n;h>=b;h--){//由于w越大，h越小，所以我们让h从大到小推
		while(w<=m&&minh[w]>h)w+=2;//增加w到minh[w]<=h为止
		minw[h]=w;//这就是minw的值啦
	}

这样的话，我们就把$w$和$h$的值限定在一个范围内啦！

不过，这里面还有很多不符合要求的情况，怎么办呢？

看图~

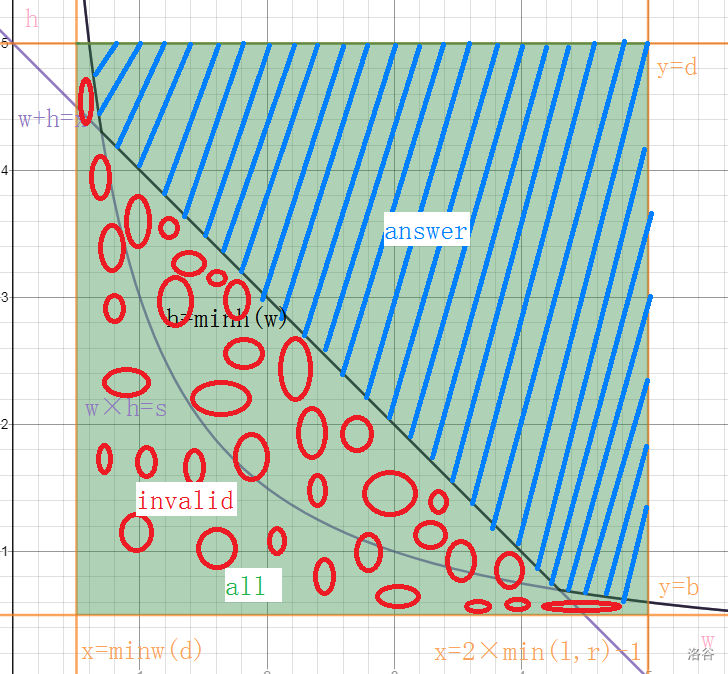
蓝色阴影的 $\color{blue}\text{answer}$ 区域——我们要求的答案

绿色的 $\color{green}\text{all}$ 区域——刚才限定出的范围

红色圈圈的 $\color{red}\text{invalid}$ 区域——不符合要求的地方

也就是说：$\color{blue}\text{answer}\color{black}=\color{green}\text{all}\color{black}-\color{red}\text{invalid}$

也就是说，我们只需要求出 $\color{red}\text{invalid}$ 区域就可以啦！

那怎么求呢？我们观察一下 $\color{blue}\text{answer}$ 区域和 $\color{red}\text{invalid}$ 区域的那条黑色分界线，你会有一个惊奇的发现：

这不就是 $\min h$ 的值嘛！！！！

所以：$\color{red}\text{invalid}\large\color{black}=\sum\limits_{i=\min w(d)}^{2\times\min(l,r)-1} \min h(i) $

貌似是一段……区间和？

那就简单了：还是用前缀和来解决问题！

先处理出$\min h$的前缀和：

sminh[w]=sminh[w-2]+minh[w];//因为w只能是奇数所以是-2

然后再用刚才的结论解决问题：

	long long ans=0;//注意long long
	for(int i=1;i<=n;i++){//枚举中心点
		for(int j=1;j<=m;j++){
			if(!wyx[i][j])continue;//只有这里是1的时候才参加统计
			long long h=sd[i][j];//h的最大范围（为了后面的invalid区域好算，h的下界直接变成0了，反正到头来还要被减掉）
			long long lw=minw[h],rw=1ll*2*min(sl[i][j],sr[i][j])-1;//w的最小范围和最大范围
			if(rw>=lw&&h>=b)//要保证有答案才能算（否则你整出来个负数是啥情况）
			ans+=1ll*(rw-lw+2)/2*(h+1)-(sminh[rw]-sminh[lw-2]);//answer=all-invalid，一些+1，-2这样的细节需要注意下
		}
	} 

---

完整代码：

#include<iostream>
#include<cstdio>
#include<cmath>
using namespace std;
bool wyx[3005][3005];
long long sl[3005][3005],sr[3005][3005],sd[3005][3005]; 
long long minh[3005],sminh[3005],minw[3005];
int n,m,a,b,s,x;
long long ans=0;
int main(){
	ios::sync_with_stdio(false);//关闭同步流
	cin.tie(0);cout.tie(0);
	cin>>n>>m>>a>>b>>s>>x;
	a=max(a,3),b=max(b,2);//说好的w>=3,h>=2
	for(int i=1;i<=n;i++){
		for(int j=1;j<=m;j++){
			char c;
			cin>>c;
			wyx[i][j]=c-'0';//输入
		}
	}
  //算出三个方向的前（后）缀和
	for(int i=1;i<=n;i++){
		for(int j=1;j<=m;j++)
		if(wyx[i][j])sl[i][j]=sl[i][j-1]+1;
	}
	for(int i=1;i<=n;i++){
		for(int j=m;j>0;j--)
		if(wyx[i][j])sr[i][j]=sr[i][j+1]+1;
	}
	for(int i=n;i>0;i--){
		for(int j=1;j<=m;j++)
		if(wyx[i][j])sd[i][j]=sd[i+1][j]+1;
	}	
	int w;		
	for(w=a+!(a&1);w<=m;w+=2){
		minh[w]=max(b,max(x-w,(int)(ceil(s*1.0/w))));//运用限制条件算出minh
		sminh[w]=sminh[w-2]+minh[w];		            
	}
	w=a+!(a&1);
	for(int h=n;h>=b;h--){
		while(w<=m&&minh[w]>h)w+=2;//运用minh算出minw
		minw[h]=w;
	}
	long long ans=0;
	for(int i=1;i<=n;i++){
		for(int j=1;j<=m;j++){
			if(!wyx[i][j])continue;
			long long h=sd[i][j];
			long long lw=minw[h],rw=1ll*2*min(sl[i][j],sr[i][j])-1;
			if(rw>=lw&&h>=b)
			ans+=1ll*(rw-lw+2)/2*(h+1)-(sminh[rw]-sminh[lw-2]);//分析算出ans（实际上可以说是容斥原理）
		}
	} 
	cout<<ans;
}

最后的最后：

1. 这个题的前身：U95387 TLE

2. yrz最近的心里话，真的……