自动搬运

查看原文

来自洛谷，原作者为

	tzc_wk **

搬运于2025-08-24 22:19:44，当前版本为作者最后更新于2021-01-10 00:23:14，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

首先我们知道，单次询问，树上路径的问题可以用点分治解决。

但如果加上什么 $q$ 次询问之类的东西怎么办呢？比如说这题。

显然每次都跑一遍点分治时间复杂度肯定吃不消。

考虑把点分治的过程离线下来，将当前树的重心与上一层的树的重心连边，这样就可以得到一棵树，我们称之为“点分树”

比如说我们有如下图所示的树：

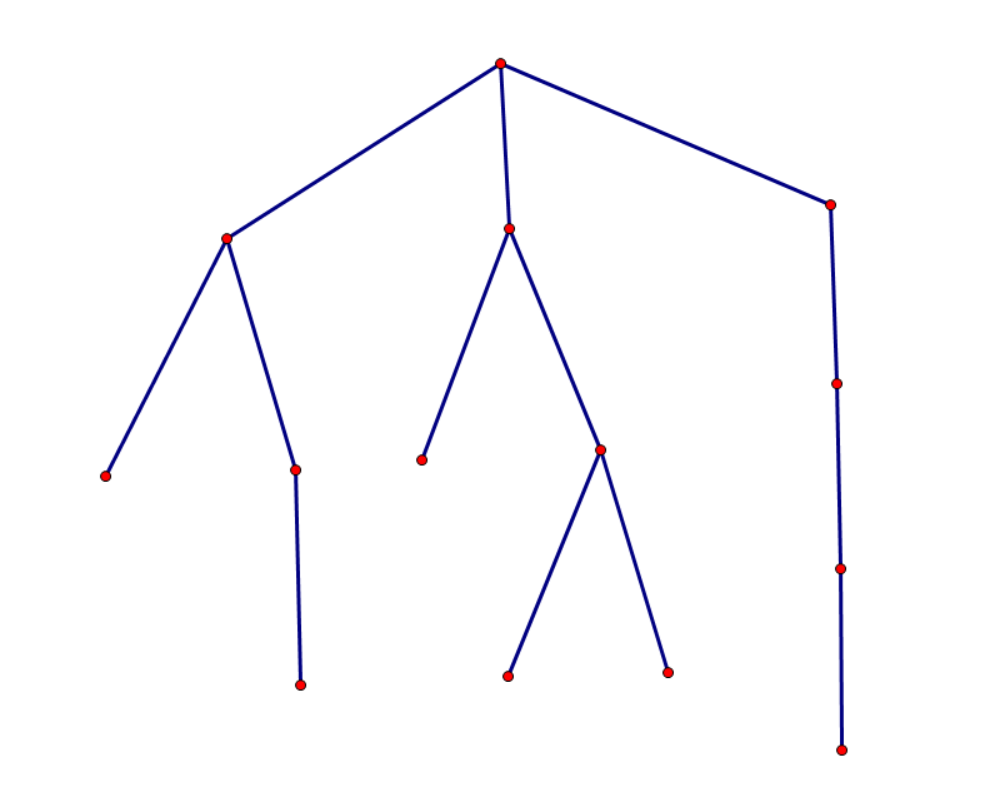
建出点分树来如下图所示：

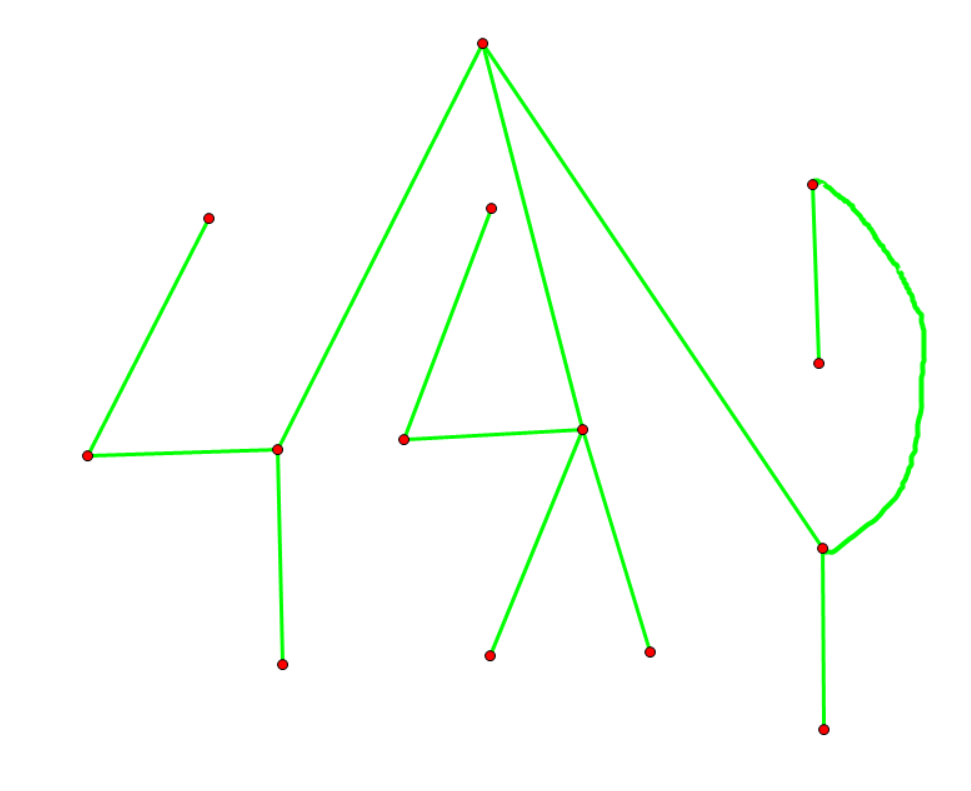
很明显，我们建出的点分树与原树几乎没有联系，父子关系完全被打乱了，也无法通过两点在点分树上的距离算出它们在原树上的距离。甚至有可能某两点在点分树上是父子关系，在原树上相隔十万八千里，或者某两点在原树上是父子关系，在点分树上相隔十万八千里（当然只是相对来说）。

那么这棵树对于我们做题有什么帮助呢？

有的问题我们不是非常关心树的形态特点，比如路径问题，联通块问题，寻找关键点问题等等，以路径问题为例，我们不一定非得查到 $p,q$ 的 LCA 才可以处理 $p,q$ 的路径信息，相反，我们可以随便从这个路径上寻找一个分割点 $t$，只要我们可以快速的处理 $p$ 到 $t$ 和 $q$ 到 $t$ 的信息，我们就可以处理 $p$ 到 $q$ 的信息。

而点分树恰恰就是对原树做了这样的映射。

它有以下性质：

1. 它的高度与点分治的深度一样，只有 $\log n$ 级别，这个性质很关键，由于它的高度只有 $\log n$，所以我们可以搞出各种各样在一般树论里过不去的暴力做法，比如说对每个点开个包含子树中所有点的 vector，空间复杂度也只有。
2. 对于任意两点 $u,v$，唯一可以确定的是 $u,v$ 在点分树上的 LCA 一定在 $u\to v$ 的路径上。换句话说，$dis(u,v)=dis(u,lca)+dis(lca,v)$。

回到这题来，我们要求 $\sum\limits_{dis(x,y)\leq k}a_y$。

考虑枚举 $x,y$ 在点分树上的 LCA $z$（这显然是 $\log n$ 级别的），根据上面的推论有 $dis(x,y)=dis(x,z)+dis(y,z)$。

故 $ans=\sum\limits_{dis(x,z)+dis(z,y)\leq k\& LCA(x,y)=z}a_y=\sum\limits_{dis(z,y)\leq k-dis(x,z)\&LCA(x,y)=z}a_y$

考虑什么样的 $y$ 满足 $LCA(x,y)=z$，显然符合要求 $y$ 组成的集合就是 $z$ 的子树抠掉 $z$ 在 $x$ 方向上的儿子 $s$ 的子树。而我们要求这个点集中到 $z$ 的距离 $\leq k-dis(x,z)$ 的点权和。显然可以拿 $z$ 的子树内到 $z$ 的距离 $\leq k-dis(x,z)$ 的点权和 $-$ $s$ 子树中到 $z$ 的距离 $\leq k-dis(x,z)$ 的点权和。

对每个点 $x$ 建一棵动态开点线段树，下标为 $i$ 的位置维护 $x$ 子树内所有 $dis(x,z)=i$ 的 $a_z$ 的和。

那么求 $z$ 子树内到 $z$ 的距离 $\leq k-dis(x,z)$ 的点权和就在对应线段树上查个区间和就 ok 了。

那 $z$ 在 $x$ 方向上的儿子 $s$ 的子树怎么办呢？

初学点分树的萌新（例如我）很容易进入一个误区，那就是这东西可以在 $s$ 对应的线段树上查 $[0,k-dis(x,z)-1]$ 的和。但这显然是错的，因为两点在点分树上的距离与两点在原树上的距离没有一丁点联系。到 $s$ 距离 $\leq k-dis(x,z)-1$，并不意味着到 $z$ 距离 $\leq k-dis(x,z)$。

那么正解是什么呢？考虑对于每个点再建立一棵动态开点线段树，线段树上下标为 $i$ 的位置维护 $x$ 子树内到 $fa_x$ 距离 $=i$ 的点权和。解决 $z$ 在 $x$ 方向上的儿子 $s$ 的子树的问题只需在点 $s$ 的线段树上查询 $[0,k-dis(x,z)]$ 的和就行了。

#include <bits/stdc++.h>
using namespace std;
#define fi first
#define se second
#define fz(i,a,b) for(int i=a;i<=b;i++)
#define fd(i,a,b) for(int i=a;i>=b;i--)
#define ffe(it,v) for(__typeof(v.begin()) it=v.begin();it!=v.end();it++)
#define fill0(a) memset(a,0,sizeof(a))
#define fill1(a) memset(a,-1,sizeof(a))
#define fillbig(a) memset(a,63,sizeof(a))
#define pb push_back
#define ppb pop_back
#define mp make_pair
template<typename T1,typename T2> void chkmin(T1 &x,T2 y){if(x>y) x=y;}
template<typename T1,typename T2> void chkmax(T1 &x,T2 y){if(x<y) x=y;}
typedef pair<int,int> pii;
typedef long long ll;
template<typename T> void read(T &x){
	x=0;char c=getchar();T neg=1;
	while(!isdigit(c)){if(c=='-') neg=-1;c=getchar();}
	while(isdigit(c)) x=x*10+c-'0',c=getchar();
	x*=neg;
}
const int MAXN=1e5;
const int MAXP=5e6;
const int LOG_N=17;
const int INF=1e9;
int n,qu,a[MAXN+5];
int hd[MAXN+5],to[MAXN*2+5],nxt[MAXN*2+5],ec=0;
void adde(int u,int v){to[++ec]=v;nxt[ec]=hd[u];hd[u]=ec;}
int fa[MAXN+5][LOG_N+2],dep[MAXN+5];
void dfs0(int x,int f){
	fa[x][0]=f;
	for(int e=hd[x];e;e=nxt[e]){
		int y=to[e];if(y==f) continue;
		dep[y]=dep[x]+1;dfs0(y,x);
	}
}
int getlca(int x,int y){
	if(dep[x]<dep[y]) swap(x,y);
	for(int i=LOG_N;~i;i--) if(dep[x]-(1<<i)>=dep[y]) x=fa[x][i];
	if(x==y) return x;
	for(int i=LOG_N;~i;i--) if(fa[x][i]!=fa[y][i]) x=fa[x][i],y=fa[y][i];
	return fa[x][0];
}
int getdis(int x,int y){return dep[x]+dep[y]-(dep[getlca(x,y)]<<1);}
int siz[MAXN+5],mx[MAXN+5],cent=0;
bool vis[MAXN+5];
void findcent(int x,int f,int tot){
	siz[x]=1;mx[x]=0;
	for(int e=hd[x];e;e=nxt[e]){
		int y=to[e];if(y==f||vis[y]) continue;
		findcent(y,x,tot);chkmax(mx[x],siz[y]);siz[x]+=siz[y];
	} chkmax(mx[x],tot-siz[x]);
	if(mx[x]<mx[cent]) cent=x;
}
int dfa[MAXN+5];
void divcent(int x,int tot){
//	printf("%d\n",x);
	vis[x]=1;
	for(int e=hd[x];e;e=nxt[e]){
		int y=to[e];if(vis[y]) continue;
		cent=0;int sz=(siz[y]<siz[x])?siz[x]:(tot-siz[x]);
		findcent(y,x,sz);dfa[cent]=x;divcent(cent,sz);
	}
}
struct segtree{
	int rt[MAXN+5],ncnt=0;
	struct node{int ch[2],val;} s[MAXP+5];
	void modify(int &k,int l,int r,int p,int x){
		if(!k) k=++ncnt;
		if(l==r){s[k].val+=x;return;}
		int mid=(l+r)>>1;
		if(p<=mid) modify(s[k].ch[0],l,mid,p,x);
		else modify(s[k].ch[1],mid+1,r,p,x);
		s[k].val=s[s[k].ch[0]].val+s[s[k].ch[1]].val;
	}
	int query(int k,int l,int r,int ql,int qr){
		if(!k) return 0;
		if(ql<=l&&r<=qr) return s[k].val;
		int mid=(l+r)>>1;
		if(qr<=mid) return query(s[k].ch[0],l,mid,ql,qr);
		else if(ql>mid) return query(s[k].ch[1],mid+1,r,ql,qr);
		else return query(s[k].ch[0],l,mid,ql,mid)+query(s[k].ch[1],mid+1,r,mid+1,qr);
	}
} w1,w2;
void modify(int x,int v){
	int cur=x;
	while(cur){
		w1.modify(w1.rt[cur],0,n-1,getdis(cur,x),v);
		if(dfa[cur]) w2.modify(w2.rt[cur],0,n-1,getdis(dfa[cur],x),v);
		cur=dfa[cur];
	}
}
int query(int x,int k){
	int cur=x,pre=0,ret=0;
	while(cur){
		if(getdis(cur,x)>k){
			pre=cur;cur=dfa[cur];continue;
		}
		ret+=w1.query(w1.rt[cur],0,n-1,0,k-getdis(cur,x));
		if(pre) ret-=w2.query(w2.rt[pre],0,n-1,0,k-getdis(cur,x));
		pre=cur;cur=dfa[cur];
	} return ret;
}
int main(){
	scanf("%d%d",&n,&qu);
	for(int i=1;i<=n;i++) scanf("%d",&a[i]);
	for(int i=1;i<n;i++){int u,v;scanf("%d%d",&u,&v);adde(u,v);adde(v,u);}
	dfs0(1,0);for(int i=1;i<=LOG_N;i++) for(int j=1;j<=n;j++)
		fa[j][i]=fa[fa[j][i-1]][i-1];
	mx[0]=INF;cent=0;findcent(1,0,n);divcent(cent,n);
//	for(int i=1;i<=n;i++) printf("%d\n",dfa[i]);
	for(int i=1;i<=n;i++) modify(i,a[i]);
	int preans=0;
	while(qu--){
		int opt,x,y;scanf("%d%d%d",&opt,&x,&y);
		x^=preans;y^=preans;
		if(opt==0){preans=query(x,y);printf("%d\n",preans);}
		else{modify(x,y-a[x]);a[x]=y;}
	}
	return 0;
}