自动搬运

查看原文

来自洛谷，原作者为

	ahawzlc 任何一个伟大的计划，都有一个微不足道的开始

搬运于2025-08-24 22:15:46，当前版本为作者最后更新于2021-07-27 16:34:40，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

思路：搜索+剪枝。

本人在撰写这篇题解之前，在网络上搜索过别的题解，发现仅此一篇题解。在学习理解该题解的基础上编写了此题的代码，因此思路上很相像。以下为自己理解的内容，请放心食用。

首先，审题之后，我们可以发现山羊的移动就是从 $(x,y,z)$ 到 $(x\pm1,y,z)$ $(x,y\pm1,z)$ $(x,y,z\pm1)$ 。这是典型的三维迷宫问题，数据范围 $1500 \approx 11 \times 11 \times 12$，肯定用搜索来解决。

在这个题中，我们考虑直接枚举战舰放置的位置。如果我们枚举一对点，这两个点能同时放置上战舰，有两种情况：

1. 这两艘战舰互不影响。
2. 这两艘战舰扩展出的地方接壤。

对于第一种情况，考虑放置战舰的点所在的联通块，如果两个联通块没有交界，显然满足互不影响的条件。

对于第二种情况，可以画图理解。

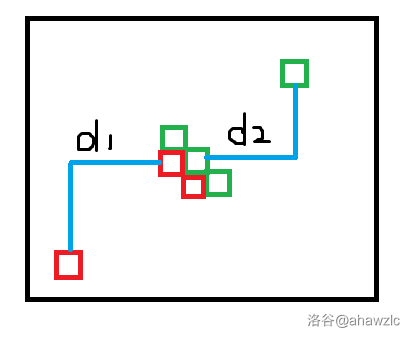
上图举了一个二维的平面为例。

显然有一个结论，如果两个联通块有交界，记交界处的点与战舰所在位置的曼哈顿距离分别为 $d1,d2$ ，则有 $d1=d2$ 或者 $d1=d2+1$ 。否则该位置一定不可能出现交界。

很显然这是一个剪枝，记做剪枝 1 。

所以我们可以根据这个条件，先预处理出选取每个点会导致哪些点不能选。

还有另外两个常见的剪枝。

剪枝 2 是如果当前点被选中后，会导致某个颜色的战舰无法被安放，直接回溯。显然这种情况下怎么搜也搜不到解。

剪枝 3 是搜索限制条件多的点，这个可以处理出来。

同时，在看到数据范围是积的形式后，肯定需要把三维点转化成一维的点。

Code：

#include<bits/stdc++.h>
using namespace std;
const int NN=1503;
inline int read() {
	int sum=0,w=1;
	char ch=getchar();
	while(ch<'0'||ch>'9') {
		if(ch=='-') w=-1;
		ch=getchar();
	}
	while(ch>='0'&&ch<='9') {
		sum=(sum<<3)+(sum<<1)+ch-'0';
		ch=getchar();
	}
	return sum*w;
}
inline int get_c() {
	char ch=getchar();
	while(ch<'a'||'z'<ch) ch=getchar();
	return ch-'a';
}
const int dx[6]={-1,1,0,0,0,0},dy[6]={0,0,-1,1,0,0},dz[6]={0,0,0,0,-1,1};//移动方向
int n,m,k,col,tot,rk[NN],pos[NN],siz[26],tmp[NN],res[26];
//col表示颜色总数，tot是将三维点转化为一维点后的点数
//rk表示点限制数目的排名，pos是rk的逆数组，tmp是点被访问的次数
//siz表示该颜色里点的数量，res表示该颜色剩余未访问的点的数量 
int c[NN];//点的颜色
int s[26],top;//存储答案的栈
vector<int> v[NN];//限制
int cnt,h[NN*NN],nxt[NN*NN],to[NN*NN];//存边（如果选了该点，哪些点不能选） 
bool vis[26];//该颜色是否被访问过/使用过（一数组两用） 
void add(int x,int y) {nxt[++cnt]=h[x];to[cnt]=y;h[x]=cnt;}//加边 
struct node {
	int x,y,z;
	node() {}
	node(int x,int y,int z):x(x),y(y),z(z) {}
};//三维点 
vector<node> g[26][26];//边界上的点 
int _abs(int x) {return x<0?-x:x;}//手写绝对值 
bool cmp(const int &x,const int &y) {return v[x].size()>v[y].size();}//根据限制多少排序 
int N(const node &p) {return p.z*n*m+p.y*n+p.x;}//三维点化一维点 
node P(const int &t) {return node(t%n,t/n%m,t/n/m);}//一维点化一维点 
int dist(const node &a,const node &b) {return _abs(a.x-b.x)+_abs(a.y-b.y)+_abs(a.z-b.z);}//曼哈顿距离 
bool range(const int &x,const int &y,const int &z) {return (x<0||x>=n||y<0||y>=m||z<0||z>=k);}//是否出界 

void build() {//存储图上的边界点 
	for(int x=0;x<n;x++) 
		for(int y=0;y<m;y++) 
			for(int z=0;z<k;z++) {
				int now=get_c();
				siz[now]++,c[N(node(x,y,z))]=now;//一般读入 
				if(!vis[now]) col++,vis[now]=1;//颜色被使用了 
			}
	for(int x=0;x<n;x++) 
		for(int y=0;y<m;y++) 
			for(int z=0;z<k;z++) 
				for(int t=0;t<6;t++) {
					int xx=x+dx[t],yy=y+dy[t],zz=z+dz[t];
					if(range(xx,yy,zz)) continue;
					node a=node(x,y,z),b=node(xx,yy,zz);
					if(c[N(a)]==c[N(b)]) continue;
					g[c[N(a)]][c[N(b)]].push_back(a);//交界点 
				}
}
void init() {//预处理 
	for(int i=0;i<tot;i++) 
		for(int j=i+1;j<tot;j++) {
			if(c[i]==c[j]) {v[i].push_back(j),v[j].push_back(i);continue;}//联通块内显然不能放 
			if(!g[c[i]][c[j]].size()) continue;//莫得交界 
			node a=P(i),b=P(j);
			for(int t=0;t<g[c[i]][c[j]].size();t++) {
				bool flag=0;
				node aa=g[c[i]][c[j]][t];
				for(int w=0;w<6;w++) {
					int xx=aa.x+dx[w],yy=aa.y+dy[w],zz=aa.z+dz[w];
					if(range(xx,yy,zz)) continue;
					node bb=node(xx,yy,zz);
					if(c[N(bb)]!=c[j]) continue;//拓展后的点不在一个联通块，说明没出界，没问题 
					int dis1=dist(a,aa),dis2=dist(b,bb);
					if(dis1==dis2) continue;//曼哈顿距离相等，没问题 
					if(_abs(dis1-dis2)>1) {flag=1;break;}//曼哈顿距离太大 
					if(c[i]<c[j]&&dis1<dis2) {flag=1;break;}//优先级问题 
					if(c[i]>c[j]&&dis1>dis2) {flag=1;break;}//同上 
				}
				if(flag) {v[i].push_back(j),v[j].push_back(i);break;}//添加上述三种可能的限制 
			}
		}
}
bool dfs(int x,int sum) {
	if(sum==col) return 1;//颜色选完了 
	if(tmp[rk[x]]) return dfs(x+1,sum);//这个点被访问过了 
	vis[c[rk[x]]]=1;//颜色被访问过了 
	s[top++]=rk[x];res[c[rk[x]]]--;//入栈、该颜色剩余的点减少 
	bool ok=1;
	for(int i=h[rk[x]];i;i=nxt[i]) {
		int y=to[i];
		if(!tmp[y]) {
			res[c[y]]--;//继续减少可用点 
			if(!vis[c[y]]&&!res[c[y]]) ok=0;//不能放置战舰了，剪枝2 
		}
		tmp[y]++;//这个点被访问过了 
	}
	if(ok&&dfs(x+1,sum+1)) return 1;//利用&&的短路性质，在能放置战舰的前提下继续向下一层搜索 
	for(int i=h[rk[x]];i;i=nxt[i]) {//回溯 
		int y=to[i];
		tmp[y]--;
		if(!tmp[y]) res[c[y]]++; 
	}
	bool flag=0;
	top--;//回溯出栈 
	vis[c[rk[x]]]=0;
	if(res[c[rk[x]]]) flag=dfs(x+1,sum);//如果还能放，尝试该层别的放法。 
	res[c[rk[x]]]++;//回溯 
	return flag;
}
int main() {
	int T=read();
	while(T--) {
		n=read(),m=read(),k=read();
		tot=n*m*k;
		build(),init(); 
		for(int i=0;i<tot;i++) rk[i]=i;
		sort(rk,rk+tot,cmp);
		for(int i=0;i<tot;i++) pos[rk[i]]=i;//记录名次和名次的逆 
		for(int i=0;i<tot;i++) 
			for(int j=0;j<v[i].size();j++) 
				if(pos[v[i][j]]>pos[i]) add(i,v[i][j]);//限制多的向限制少的连边 
		for(int i=0;i<26;i++) res[i]=siz[i],vis[i]=0;//能选的数量等于该颜色点的数量，重置vis 
		dfs(0,0);
		for(int i=0;i<top;i++) {//不把栈当栈用QWQ 
			node p=P(s[i]);
			printf("%c %d %d %d\n",c[s[i]]+'a',p.x,p.y,p.z);//输出答案 
		}
		for(int i=0;i<tot;i++) tmp[i]=0,v[i].clear(),h[i]=0;//各种清空 
		for(int i=0;i<26;i++) for(int j=0;j<26;j++) g[i][j].clear();
		for(int i=0;i<26;i++) vis[i]=siz[i]=0;
		cnt=col=top=0;
	}
	return 0;
}