自动搬运

查看原文

来自洛谷，原作者为

	harryzhr AFO

搬运于2025-08-24 22:13:17，当前版本为作者最后更新于2020-09-20 17:27:10，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

---

蒟蒻的第一篇题解

题目传送门 洛谷P5677 [GZOI2017]配对统计

前情提要

此题要用到树状数组，没有学过的朋友可以先去做做洛谷P3374 【模板】树状数组 1

简要题意

一组数 $a_1,a_2,\cdots,a_n$

一组配对 $(x,y)$ 是好的配对（以后简称好对）当且仅当 $(x,y)$ 使得 $\left\vert a_x-a_y\right\vert$ 最小。

多组询问 $[l,r]$ 中好对的个数。

思路

寻找所有好对

首先我们来理解题意：

$\left\vert a_x-a_y\right\vert \le \left\vert a_x-a_i\right\vert(i\ne x)$ ，就是说 $a_x$ 和 $a_y$ 对于 $a_x$ 是相差最小两个数，放到数轴上就是挨得最近的两个数。

所以就想到了排序，这样每个数可能的好对就是它和它两边的两个数。

举个栗子：

$$3,9,11,4,8,6$$

编号

$$1,2,3,4,5,6$$

排序过后就变成

$$3,4,6,8,9,11$$

对应的编号是

$$1,4,6,5,2,3$$

对于每一个数，判断一下它与它左右两边的数的差的绝对值：

• 如果相等，那么就是两个好的配对（左右两边都是好对），以6为例：

$\left\vert 6-4\right\vert = \left\vert 6-8\right\vert$ 6和4对应的好对为 $(6,4)$ ，6和8对应的好对为 $(6,5)$。

• 如果不相等，那么只有绝对值之差更小的一对，以4为例：

$\left\vert 4-3\right\vert < \left\vert 4-6\right\vert$ 只有4和3的好对 $(4,1)$ 。

• 当然两边的数只有唯一的一对

3和4对应 $(1,4)$ ，11和9对应 $(3,2)$。

注：为方便以后查询，统一把好对中出现位置较小的那个放在前面（就是说6和8对应的好对 $(6,5)$ 记为 $(5,6)$ ）。

要注意的是，如果一个配对 $(x,y)$ 是好对， $(y,x)$ 不一定是好对，如9和11： $(3,2)$ 是好对，而 $(2,3)$ 就不是。

数据约束中说到当$i \ne j,a_i \ne a_j$，即$a$中没有相同的元素，这样就保证了这个配对判断的正确性。

至此我们已经找到了所有的配对，时间复杂度 $O(n \log n)$ （瓶颈在排序）。

查询所有询问

每次询问都是区间查询，很容易想到树状数组（当然还有线段树），也就是查询所有左右端点都在$[l,r]$内的好对。

但是怎么查呢？

请仔细思考后再继续阅读。

---

你会发现，如果把所有的好对都放进树状数组里不太好查。

那我们就不要一次性把所有的好对都放进去呗。

也就是说，对于每次查询，我们只把右端点在 $(0,r]$ 内的好对放进树状数组。

树状数组 $tree[i]$ 表示左端点在 $[i-\operatorname{lowbit}(i)+1 , i]$ 内的所有好对的的个数。

已经放入的好对个数，减去左端点在 $(0,l-1]$ 内的好对（也就是减去 $\operatorname{query}(l-1)$ ），就可以得到答案了。

再举栗子：

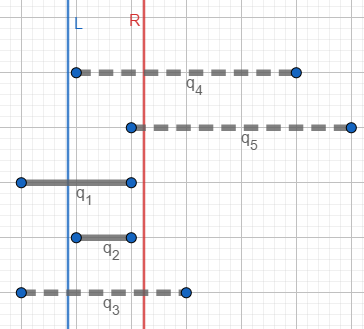
实线表示该好对在树状数组中，虚线表示该好对还未放入树状数组。

待查询的区间 $[L,R]$ 如图所示，此时只有 $q_1,q_2$ 两个好对在R左侧，再减去左端点在L左侧的 $q_1$ ，就得到 $[L,R]$ 内的好对数目：1个（ $q_2$ ）。

我们再将所有的好对和所有的询问，都按右端点从小到大排个序。

每次R右移，就将右端点小于等于R的所有好对，都加入到树状数组里，再减去左端点在 $(0,l-1]$ 内的好对个数就是答案。

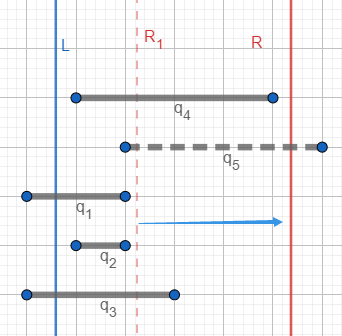
此时R右移， $q_3,q_4$ 被放入树状数组，再减去左端点在L左侧的 $q_1,q_3$ ，就得到 $[L,R]$ 内的好对数目：2个（$q_2,q_4$）。

遍历每个询问$O(n)$，每次查询$O(\log n)$,总时间复杂度$O(n \log n)$。

统计答案

因为答案的计算方法很奇葩特殊， $\sum\limits_{i=1}^mAns_i \times i$ 。

所以我们在给询问排序的时候也要记录下它原先的 $i$ （代码中为 $pos$ ）。

$Ans_i$ 的计算方法上文已经讲得很清楚了，这里不再多说。

整体时间复杂度 $O(n \log n)$ 。

亲身经历告诉你们一定要开long long!!!

关于hack

新增的hack中 $n=1$，如果不特判的话会出现 $i+=lowbit(i)$ 而 $i=0$，从而死循环，下面的代码已经可以通过 hack

上代码：

#include <iostream>
#include <cstdio>
#include <algorithm>
#define ll long long
using namespace std;
int lowbit(int x){	return x & (-x);}
int n,m;
ll tree[300001];
void add(int pos){	//单点修改（每次只用加1） 
	while(pos<=n)	
		tree[pos]++,pos+=lowbit(pos);
}
int Query(int num){
	ll sum=0;
	while(num>0)
		sum+=tree[num],num-=lowbit(num);
	return sum;
}
//以上为树状数组的单点修改区间查询 
struct Num{	
	ll num;	int pos;	//原数组 
}a[300001];
bool cmp(Num a1,Num a2){return a1.num<a2.num;}	//结构体排序 
struct Pair{
	int l,r;			//好对 
}pairr[600002];
int paircnt=0;		//记录好对个数 
void add_pair(Num a1,Num a2){
	int l=min(a1.pos,a2.pos) , r=max(a1.pos,a2.pos);
		//为了方便查询，统一把好对中出现位置较小的那个放在前面 
	pairr[++paircnt].l=l;
	pairr[paircnt].r=r;
	return ;
}
bool cmpPair(Pair a1,Pair a2){		//对所有的好对按右端点从小到大排序 
	if(a1.r!=a2.r)	return a1.r<a2.r;
	else return a1.l<a2.l;
}
struct Questions{
	int l,r,pos;		//询问 
}question[300001];
bool cmpQestions(Questions a1,Questions a2){	//对所有的询问按右端点从小到大排序 
	if(a1.r!=a2.r)	return a1.r<a2.r;
	else return a1.l<a2.l;
}
int main(){
	scanf("%d %d",&n,&m);
    	if(n==1){puts("0");return 0;}//新增的hack
	for(int i=1 ; i<=n ; i++){
		scanf("%lld",&a[i].num);
		a[i].pos=i;			//记录下该数在原先序列里的位置，排完序后方便添加配对 
	}
	sort(a+1,a+1+n,cmp);	//排序 
	add_pair(a[1],a[2]);	//首位特殊处理
	add_pair(a[n],a[n-1]);	//末尾特殊处理
	for(int i=2 ; i<n ; i++){
		int ldif = a[i].num-a[i-1].num , rdif = a[i+1].num-a[i].num;	//左边的差 和 右边的差 
		if(ldif<rdif)		add_pair(a[i],a[i-1]);		//左边差更小，只有左边的一对 
		else if(ldif==rdif)	add_pair(a[i],a[i-1]),add_pair(a[i],a[i+1]);
														//两边差更小，有两对 
		else				add_pair(a[i],a[i+1]);		//右边差更小，只有右边的一对 
	}
	sort(pairr+1 , pairr+1+paircnt , cmpPair);	//对所有的好对按右端点从小到大排序
	for(int i=1;i<=m;i++){
		scanf("%d %d", &question[i].l ,&question[i].r);
		question[i].pos=i;
	}
	sort(question+1 , question+1+m , cmpQestions);//对所有的询问按右端点从小到大排序
	ll ans=0;		//ans为最终答案
	for(int i=1,j=1 ; i<=m ; i++){	//i为当前询问，j为当前待入树状数组的好对 
		while(pairr[j].r<=question[i].r && j<=paircnt){
			add(pairr[j].l);		//如果当前好对的右端点在当前询问的右端点内，就加入树状数组 
			j++;
		}
		ans+=1ll * question[i].pos * (j-1- Query(question[i].l-1) );	//计算答案 
	}
	printf("%lld",ans);	//输出 
	return 0;
}