自动搬运

查看原文

来自洛谷，原作者为

	Graphcity 循此苦旅，终抵繁星。

搬运于2025-08-24 22:11:59，当前版本为作者最后更新于2022-08-02 10:04:41，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

---

题意：给定一棵树，边带权，每个点有黑白两种颜色，你需要支持翻转某个点的颜色，或者查询所有黑点到某一条链的距离之和。

---

分两种情况讨论：在 LCA 的子树内，在 LCA 的子树外。

为了方便，我们规定：

• $d_i$ 为结点 $i$ 到根结点的距离（也就是深度）
• $s_i$ 为结点 $i$ 所在子树的黑点个数
• $sd_i$ 为结点 $i$ 所在子树中黑点的深度之和
• $sum$ 为整棵树中的黑点个数

先看第一种情况：（ 给定的链为 $a\to d\to f$ ）

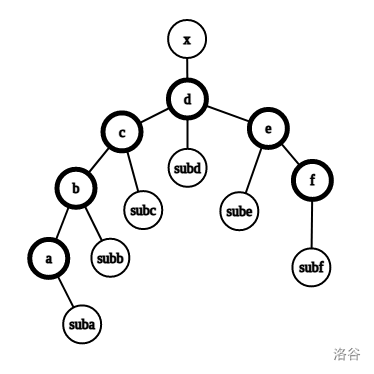
我们分别计算每个链上结点作为 LCA 时对答案的贡献：

$+$	$-$
$sd_a-d_as_a$
$sd_b-d_bs_b$	$sd_a-d_bs_a$
$sd_c-d_cs_c$	$sd_b-d_cs_b$
$sd_d-d_ds_d$	$sd_c-d_ds_c,\ sd_e-d_ds_e$
$sd_e-d_es_e$	$sd_f-d_es_f$
$sd_f-d_fs_f$

其中加号表示正贡献，减号表示负贡献。整理可得答案为

$$(d_b-d_a)s_a+(d_c-d_b)s_b+(d_d-d_c)s_c+(d_d-d_e)s_e+(d_e-d_f)s_f+sd_d-d_ds_d $$

再看第二种情况：

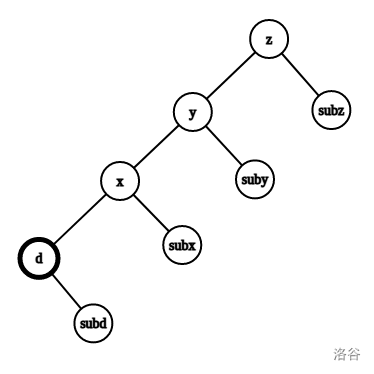
还是一样的，列表计算贡献：（ 根据 $dis(x,y)=dep_x+dep_y-2dep_{lca(x,y)}$ ）

$+$	$-$
$sd_x-2d_xs_x$	$sd_d-2d_xs_d$
$sd_y-2d_ys_y$	$sd_x-2d_ys_x$
$sd_z-2d_zs_z$	$sd_y-2d_zs_y$
$d_d(sum-s_d)$

整理可得：

$$sd_z-sd_d+d_d(sum-s_d)-2(d_xs_x+d_ys_y+d_zs_z)+2(d_xs_d+d_ys_x+d_zs_y) $$

---

可以发现，答案当中有着非常多形如 $s_i,\ sd_i,\ d_is_i,\ d_{fa_i}s_i$ 的式子。我们便可以开四棵线段树，来分别维护这四个式子的和。

每次改变结点颜色的时候，只需要修改从它到根结点的链上这四个式子的值。修改和查询都可以用树链剖分解决。

注意 $d_is_i$ 与 $d_{fa_i}s_i$ 的修改与普通线段树稍有不同。

#include<bits/stdc++.h>
#define ll long long
#define For(i,a,b) for(int i=(a);i<=(b);++i)
#define Rof(i,a,b) for(int i=(a);i>=(b);--i)
using namespace std;
typedef pair<int,int> Pair;
const int Maxn=2e5;

inline int read()
{
    int x=0,f=1;
    char ch=getchar();
    while(ch<'0' || ch>'9')
    {
        if(ch=='-') f=-1;
        ch=getchar();
    }
    while(ch>='0' && ch<='9')
    {
        x=x*10+ch-'0';
        ch=getchar();
    }
    return x*f;
}

int n,m,kazuha,all,typ[Maxn+5]; ll dep[Maxn+5],sd[Maxn+5];
int siz[Maxn+5],fa[Maxn+5],son[Maxn+5];
int dfn[Maxn+5],pre[Maxn+5],top[Maxn+5],cur;
vector<Pair> v[Maxn+5];
#define ls(x) (x<<1)
#define rs(x) (x<<1|1)

inline void dfs1(int x,int f)
{
    fa[x]=f,siz[x]=1,sd[x]=dep[x];
    for(auto i:v[x])
    {
        int y=i.first,z=i.second;
        if(y==f) continue;
        dep[y]=dep[x]+z;
        dfs1(y,x),siz[x]+=siz[y],sd[x]+=sd[y];
        son[x]=(siz[y]>siz[son[x]]?y:son[x]);
    }
}
inline void dfs2(int x,int t)
{
    top[x]=t,dfn[x]=++cur,pre[cur]=x;
    if(son[x]) dfs2(son[x],t);
    for(auto i:v[x])
    {
        int y=i.first;
        if(y==fa[x] || y==son[x]) continue;
        dfs2(y,y);
    }
}

struct SegTree
{
    ll t[Maxn*4+5],tag[Maxn*4+5],val[Maxn+5],sum[Maxn+5]; int opt;
    inline void push_up(int p) {t[p]=t[ls(p)]+t[rs(p)];}
    inline void f(int p,ll k,int len) {t[p]+=len*k,tag[p]+=k;}
    inline void f2(int p,ll k,int l,int r) {t[p]+=(sum[r]-sum[l-1])*k,tag[p]+=k;}
    inline void push_down(int l,int r,int p)
    {
        int mid=(l+r)>>1;
        f(ls(p),tag[p],mid-l+1),f(rs(p),tag[p],r-mid),tag[p]=0;
    }
    inline void push_down2(int l,int r,int p)
    {
        int mid=(l+r)>>1;
        f2(ls(p),tag[p],l,mid),f2(rs(p),tag[p],mid+1,r),tag[p]=0;
    }
    inline void Build(int l,int r,int p)
    {
        if(l==r) {t[p]=val[pre[l]]; return;}
        int mid=(l+r)>>1;
        Build(l,mid,ls(p)),Build(mid+1,r,rs(p)),push_up(p);
    }
    inline void Update(int nl,int nr,int l,int r,int p,ll k)
    {
        if(l<=nl && nr<=r) {t[p]+=(nr-nl+1)*k,tag[p]+=k; return;}
        int mid=(nl+nr)>>1; push_down(nl,nr,p);
        if(l<=mid) Update(nl,mid,l,r,ls(p),k);
        if(r>mid) Update(mid+1,nr,l,r,rs(p),k);
        push_up(p);
    }
    inline void Update2(int nl,int nr,int l,int r,int p,ll k)
    {
        if(l<=nl && nr<=r) {t[p]+=(sum[nr]-sum[nl-1])*k,tag[p]+=k; return;}
        int mid=(nl+nr)>>1; push_down2(nl,nr,p);
        if(l<=mid) Update2(nl,mid,l,r,ls(p),k);
        if(r>mid) Update2(mid+1,nr,l,r,rs(p),k);
        push_up(p);
    }
    inline ll Count(int nl,int nr,int l,int r,int p)
    {
        if(l<=nl && nr<=r) return t[p];
        int mid=(nl+nr)>>1; ll res=0;
        if(!opt) push_down(nl,nr,p);
        else push_down2(nl,nr,p);
        if(l<=mid) res+=Count(nl,mid,l,r,ls(p));
        if(r>mid) res+=Count(mid+1,nr,l,r,rs(p));
        push_up(p); return res;
    }
    inline void Modify(int x,int y,ll z)
    {
        while(top[x]!=top[y])
        {
            if(dep[top[x]]<dep[top[y]]) swap(x,y);
            Update(1,n,dfn[top[x]],dfn[x],1,z),x=fa[top[x]];
        }
        if(dep[x]>dep[y]) swap(x,y);
        Update(1,n,dfn[x],dfn[y],1,z);
    }
    inline void Modify2(int x,int y,ll z)
    {
        while(top[x]!=top[y])
        {
            if(dep[top[x]]<dep[top[y]]) swap(x,y);
            Update2(1,n,dfn[top[x]],dfn[x],1,z),x=fa[top[x]];
        }
        if(dep[x]>dep[y]) swap(x,y);
        Update2(1,n,dfn[x],dfn[y],1,z);
    }
    inline ll Find(int x,int y)
    {
        ll res=0;
        while(top[x]!=top[y])
        {
            if(dep[top[x]]<dep[top[y]]) swap(x,y);
            res+=Count(1,n,dfn[top[x]],dfn[x],1),x=fa[top[x]];
        }
        if(dep[x]>dep[y]) swap(x,y);
        res+=Count(1,n,dfn[x],dfn[y],1);
        return res;
    }
} T[4];

inline int LCA(int x,int y)
{
    while(top[x]!=top[y])
    {
        if(dep[top[x]]<dep[top[y]]) swap(x,y);
        x=fa[top[x]];
    }
    return (dep[x]<dep[y]?x:y);
}
inline void Change(int x)
{
    if(!typ[x])
    {
        T[0].Modify(x,1,1);
        T[1].Modify(x,1,dep[x]);
        T[2].Modify2(x,1,1);
        T[3].Modify2(x,1,1);
        typ[x]=1,all++;
    }
    else
    {
        T[0].Modify(x,1,-1);
        T[1].Modify(x,1,-dep[x]);
        T[2].Modify2(x,1,-1);
        T[3].Modify2(x,1,-1);
        typ[x]=0,all--;
    }
}
inline ll Query(int x,int y)
{
    int d=LCA(x,y);
    ll sdd=T[1].Count(1,n,dfn[d],dfn[d],1),szd=T[0].Count(1,n,dfn[d],dfn[d],1);
    ll s1=sdd-dep[d]*szd+T[3].Find(x,y)-T[2].Find(x,y)-szd*(dep[fa[d]]-dep[d]),s2=0;
    if(fa[d])
    {
        ll sd1=T[1].Count(1,n,1,1,1);
        s2=dep[d]*(all-szd)+sd1-sdd;
        s2=s2+2ll*T[3].Find(1,d)-2ll*T[2].Find(1,fa[d]);
    }
    return s1+s2;
}

int main()
{
    n=read(),m=read(),kazuha=read(),all=n;
    T[0].opt=0,T[1].opt=0,T[2].opt=1,T[3].opt=1;
    For(i,1,n-1)
    {
        int a=read(),b=read(),c=read();
        v[a].push_back(make_pair(b,c)),v[b].push_back(make_pair(a,c));
    }
    For(i,1,n) typ[i]=read();
    dfs1(1,0),dfs2(1,1);
    For(i,1,n) T[2].sum[i]=T[2].sum[i-1]+dep[pre[i]];
    For(i,1,n) T[3].sum[i]=T[3].sum[i-1]+dep[fa[pre[i]]];
    For(i,0,3)
    {
        if(i==0) For(j,1,n) T[i].val[j]=siz[j];
        if(i==1) For(j,1,n) T[i].val[j]=sd[j];
        if(i==2) For(j,1,n) T[i].val[j]=1ll*siz[j]*dep[j];
        if(i==3) For(j,1,n) T[i].val[j]=1ll*siz[j]*dep[fa[j]];
        T[i].Build(1,n,1);
    }
    For(i,1,n) if(!typ[i]) typ[i]=1,Change(i);
    while(m--)
    {
        int opt=read(),x=read(),y;
        if(opt==1) Change(x);
        else y=read(),printf("%lld\n",Query(x,y));
    }
    return 0;
}