自动搬运

查看原文

来自洛谷，原作者为

	liangsheng One today is worth two tomorrows.

搬运于2025-08-24 22:11:50，当前版本为作者最后更新于2019-09-23 21:07:31，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

看了一下题解,没有讲的非常详细的,第一次接触二维差分不画图的话挺难理解的

所以我来一发详细一点的题解,给像我一样的蒟蒻一点温暖

废话不多,进入正题

1. 二维前缀和 (这里引用一下别人的图,实现画不出来)

首先我们学习二维差分的之前需要先了解二维前缀和

如图:

因为是从左到右，从上到下的遍历，当要求红色部分，(0,0) 到（i, j）处的前缀和时，我们黄色部分和蓝色部分已经是已知的了，而它们重叠的部分就是绿色部分，所以把黄色和蓝色部分的结果加起来，再减去绿色部分，最后加上 (i, j) 处的值就是（i, j）位置的前缀和了。

所以，二维前缀和就是:

sum[i][j]=a[i][j]+sum[i-1][j]+sum[i][j-1]-sum[i-1][j-1]

而我们要求左上角是(x1,y1),右下角是(x2,y2)的矩形区间内的值处理出前缀和后也可以O(1)时间内求出来。

如图:

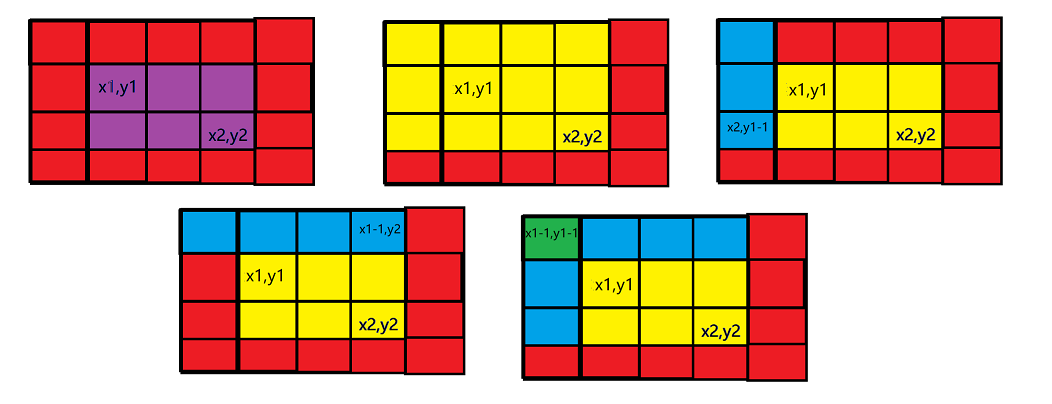
我们要求紫色部分的值，我们已知的是黄色部分的值，但它多了两个蓝色部分的值，而两个蓝色部分有重叠了个绿色部分

所以要求的区间内的值就是:

sum[x2][y2]-sum[x2][y1-1]-sum[x1-1][y2]+sum[x1-1][x2-1]

2. 二维差分

(下面是自己画的图,画的不好,将就一下)

我们以这题的样例来解释什么是二维差分

首先给出结论:

若想在点(x1,y1)到点(x2,y2)围成的矩形的每个位置增加1
则我们要进行以下操作:

设vis[i][j]:原点到点(i,j)围成的矩形的总和

   vis[x1 + 1][y1 + 1]++;
   vis[x2 + 1][y2 + 1]++;
   vis[x1 + 1][y2 + 1]--;
   vis[x2 + 1][y1 + 1]--;

我们给出根据样例的三组数据实现后的坐标轴:

黑色线段围成的矩形就是每次要加1的矩形

下面我们解释为什么要这样做:

我们就以 点(1,1) 和 点(5,5)为例讲解

首先 vis[2][2]++;

而 vis[2][2] 的值改变,谁的值会受影响呢?

很明显: i >= 2 && j >= 2的vis[i][j]的值全部都会收到影响

我们先来看 i = 2,j >= 2的情况  也就是点(1,1)到点(2,6)橙色长方形

我们令 vis[2][6]--  进行此操作后 我们会发现 
vis[2][j >= 5]的值又不会受到影响了
    
很简单,我们来证明一下: 令 j=7

     想象一下点(0,0)和点(2,7)围成的矩形	
     我们会发现 点(2,2)加的1 和点(2,6)减的1 抵消了
     故不会受影响了
     证毕
        				
这里明白后其他两处加1和减1就也能明白了

不明白的话多看几遍,深度理解

而之后的操作我在这里也给出:

int ans = 0;
for(int i = 1; i <= 1000; i++) {
   for(int j = 1; j <= 1000; j++) {
   	    vis[i][j] += vis[i - 1][j] + vis[i][j - 1] - vis[i - 1][j - 1];
        if(vis[i][j] == k) ans++;
   }
}
cout << ans << endl;

然后我给出最终 vis 数组中的值,方便加深理解

最后,给出本题的AC代码:

#include <iostream>
#include <cstring>

using namespace std;

int n, k;
int vis[1005][1005];

int main() {
    cin >> n >> k;
    int x1, y1, x2, y2;
    for(int i = 1; i <= n; i++) {
        cin >> x1 >> y1 >> x2 >> y2;
        vis[x1 + 1][y1 + 1]++;
        vis[x2 + 1][y2 + 1]++;
        vis[x1 + 1][y2 + 1]--;
        vis[x2 + 1][y1 + 1]--;
    }
    int ans = 0;
    for(int i = 1; i <= 1000; i++) {
        for(int j = 1; j <= 1000; j++) {
            vis[i][j] += vis[i - 1][j] + vis[i][j - 1] - vis[i - 1][j - 1];
            if(vis[i][j] == k) ans++;
        }
    }
    cout << ans << endl;
    return 0;
}