15011418730 LV 7 @ 2025-8-24 22:11:30

自动搬运

来自洛谷，原作者为

	Hope2075 时间的流沙，淹没梦境里的夏

搬运于2025-08-24 22:11:30，当前版本为作者最后更新于2019-08-14 18:01:23，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

出题人突然想卡掉 $O(n\log n)$ 的做法，于是加强了最后一个点的数据范围（ $1\times 10^6$ 改为 $2.5\times 10^6$ ），然后优化了一下交互库和std，但时限没改

结果就是有点卡常（不过我的std好像优化得不很好）

最后一个点std用时2.4秒（好像和之前一样QWQ）， $O(n\log n)$ 的算法约3.2秒

（借用的小粉兔的代码）

实在也没啥好办法了QWQ

题解除了代码，别的都没变

如果管理员认为不合适，请私信，我可以把数据改回去

题意：给出两个长为 $n$ 的序列 $(a_i,na_i),(b_i,nb_i)$

你需要求：

1.$\sum_{i=1}^n\sum_{j=1}^n na_i\cdot nb_j \cdot [b_j>a_i]$

也就是所有满足 $b_j>a_i$ 的 $na_i\cdot nb_j$ 之和

2.给出 $x,y,z,w$ ，如果序列 $(a_i,na_i)$ 只保留满足 $a_i$ 大小在 $a_x$ 和 $a_y$ 之间的部分，序列 $(b_i,nb_i)$ 只保留满足 $b_i$ 大小在 $b_z$ 和 $b_w$ 之间的部分，那么第一问的答案

算法1

暴力枚举 $i,j$

时间复杂度 $O(n^2q)$

期望得分4分

算法2

先对两个序列分别按照 $a_i,b_i$ 从小到大排序

这时候发现，如果对于一个 $b_i$ ，某个 $a_j$ 能产生贡献 $(j>1)$ ，那么 $a_{j-1}$ 也能产生贡献

而当 $i$ 变大时，最大的能产生贡献的 $a_j$ 的位置不会向左移动

所以，用双指针求值

从左向右枚举 $i$ 的位置，并记录满足条件的 $a_j$ 对应 $na_j$ 的和，每次移动 $i$ 后，再移动 $j$ ，把扫过的部分加上，随后更新答案，加上这个 $i$ 产生的贡献

对于之后的询问，发现对应 $a_i$ 和 $b_i$ 在一段连续的区间里，用类似的方法就能求出答案

为了方便，处理询问前，根据 $a_x$ 和 $a_y$ 的大小关系交换 $x,y$ ，根据 $b_z$ 和 $b_w$ 的大小关系交换 $z,w$

关于如何找询问在排序后序列中的位置：这部分完全可以暴力找位置，不影响复杂度

后面的部分可以把序列排序前的值记录下来，根据值进行二分

还有另外一种方法可以 $O(1)$ 找位置，在最后面讲

时间复杂度 $O(nq)$

期望得分18分

算法3

针对#3

发现 $a_i,b_i$ 都很小

所以，统计每个 $a_i,b_i$ 对应 $na_i,nb_i$ 的和

处理询问时有多种方法，其中一种是：与算法2类似，在对应区间内用双指针法处理

另一个方法在算法5中讲解

暴力找位置再求值即可

时间复杂度 $O(n+q\cdot a_i)$

期望得分11分，结合算法2期望得分29分

算法4

针对#4

发现 $q$ 很大， $n$ 很小

说明询问的总情况数很小

所以枚举所有询问，然后分别求出答案，在询问时就能做到 $O(1)$

时间复杂度 $O(n^6+q)$ 或 $O(n^5+q)$

期望得分10分，结合算法2期望得分28分

算法5

针对#5

这时候发现 $n$ 变大了

需要发现一个性质才能继续优化

以样例2为例

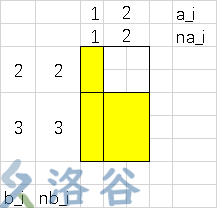
把图画出来，其中黄色格子代表可以产生贡献

考虑询问2 2 2 2

答案很明显是6

这样就能看出，实际是一个前缀和

所以，按照图中的做法弄一个二维数组，然后求二维前缀和

处理询问时，找到位置后，差分一下，就能 $O(1)$ 求出答案（找位置可能是 $O(\log n)$ ）

空间大概100MB，能开得下

也可以用类似的思路过#3：把连续的一段压成一个点，然后就能用类似的思路做了，时间复杂度是 $O(a_i^2+q)$

时间复杂度 $O(n^2+q\log n)$ 或 $O(n^2+q)$

期望得分36分，结合其它算法能得到更高的分数

算法6

对于最后两组数据， $n$ 太大了，不能直接用前缀和

这时候，使用一种类似的思路

如果 $n$ 很大，那么按照上面画出来的图可能是这样的

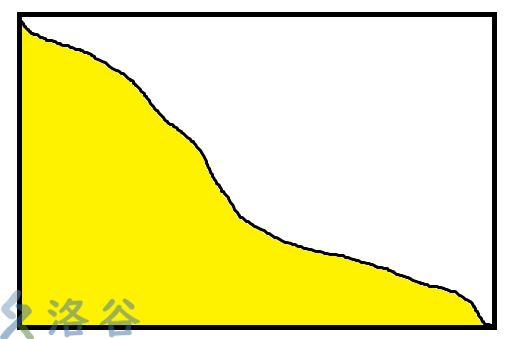
那么，求前缀和需要的部分可能有这两种情况

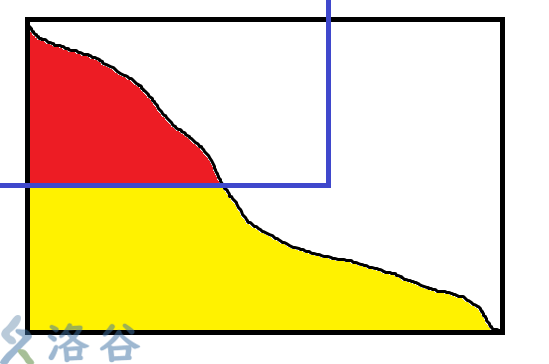
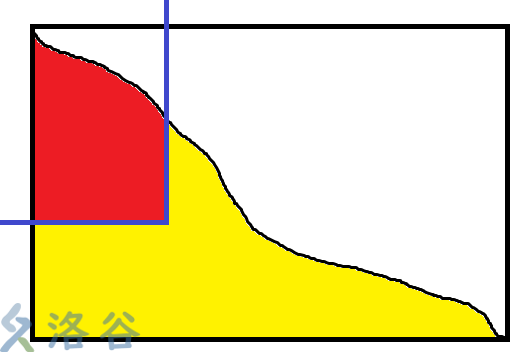
（恰好在边界归为任何一种都可以）

第一种情况： $a_i\ge b_j$

这时候，需要求的可以转化为所有满足 $k\le j$ 的 $b_k$ 产生的贡献

这部分可以用算法2的思路求，不同之处是记录每个 $b_j$ 的值

第二种情况： $a_i<b_j$

这时候可以看成一个矩形减去一块

矩形部分很容易计算，用 $na_i$ 和 $nb+j$ 的前缀和就能算出来

而减去的一块看起来很像上面一种情况

不同之处是，这部分是 $a_k$ 的值，而且是不能产生贡献的部分

这样就和上面类似了

当然，还有另外3种思路，不过基本是类似的，只是求前缀和的方向不同

时间复杂度 $O(n+q\log n)$ 或 $O(n+q)$

虽然std的内存使用约160MB，但还是请注意内存使用情况，有些写法可能就会消耗更多的空间

期望得分100分

关于 $O(1)$ 找位置

在排序的时候，先记录每个数原来的位置

排完序后，把数字相同的部分合并，然后根据原位置的信息把位置映射到新的位置

这样，就可以 $O(1)$ 找到位置了

注意：排序要用基数排序，否则复杂度会带log

~~其实出题人本来想卡带 $\log$ 的算法的，但是出题人的std常数有点大，不太好卡，于是就放过去了~~

上面一行作废，现在 $O(n\log n)$ 算法不容易卡过去

代码：

#include<cstdio>
using namespace std;
#define u32 unsigned int
#define u64 unsigned long long
int cl;
const int N=2500007;
const long long M=998244353LL;
int n,q,k;
int a[N],na[N],b[N],nb[N];
int x,y,z,u;
namespace lib{
    u64 read(){
        u64 n=0;
        char c=getchar();
        while(c<'0'||c>'9')c=getchar();
        while(c>='0'&&c<='9'){
            n=n*10+c-'0';
            c=getchar();
        }
        return n;
    }
    char r[30];
    void write(u64 num){
        if(num==0){
            putchar('0');
            return;
        }
        int t=0;
        while(num){
            r[t++]=num%10+'0';
            num/=10;
        }
        while(t)putchar(r[--t]);
    }
    u64 s;
    u64 rand(u64 l,u64 r){
        s=s*19260817+1;
        return ((s>>8)%(r-l+1)+l);
    }
    int ra,t;
    void init(){
        n=read();k=read();
        if(k<2){
            for(int i=1;i<=n;i++){
                a[i]=read();na[i]=read();
            }
            for(int i=1;i<=n;i++){
                b[i]=read();nb[i]=read();
            }
        }else{
            s=read();ra=read();
            u64 bacs=s;
            for(int i=1;i<=n;i++){
            	s=s*19260817+1;
        		a[i]=((s>>8)%ra+1);
                //a[i]=rand(1,ra);
                s=s*19260817+1;
        		//na[i]=((s>>8)%(M-1)+1);
                //na[i]=rand(1,M-1);
            }
            s=bacs;
            for(int i=1;i<=n;i++){
            	s=s*19260817+1;
        		//a[i]=((s>>8)%ra+1);
                //a[i]=rand(1,ra);
                s=s*19260817+1;
        		na[i]=((s>>8)%(M-1)+1);
                //na[i]=rand(1,M-1);
            }
            bacs=s;
            for(int i=1;i<=n;i++){
                s=s*19260817+1;
        		b[i]=((s>>8)%ra+1);
                //a[i]=rand(1,ra);
                s=s*19260817+1;
        		//nb[i]=((s>>8)%(M-1)+1);
            }
            s=bacs;
            for(int i=1;i<=n;i++){
                s=s*19260817+1;
        		//b[i]=((s>>8)%ra+1);
                //a[i]=rand(1,ra);
                s=s*19260817+1;
        		nb[i]=((s>>8)%(M-1)+1);
            }
        }
        q=read();
    }
    u64 lastans;
    u64 res;
    void reply(u64 num){
        if(k<2){
            write(num);putchar('\n');
        }else{
            res=res*233+num;
        }
        lastans^=num;
    }
    void query(){
        if(k<2){
            x=read();y=read();z=read();u=read();
        }else{
        	s=s*19260817+1;
        	x=((s>>8)%n+1);
        	s=s*19260817+1;
        	y=((s>>8)%n+1);
        	s=s*19260817+1;
        	z=((s>>8)%n+1);
        	s=s*19260817+1;
        	u=((s>>8)%n+1);
            //x=rand(1,n);y=rand(1,n);z=rand(1,n);u=rand(1,n);
        }
        if(k&1){
        	int t=lastans%n+1;
        	if((x+=t)>n)x-=n;
        	if((y+=t)>n)y-=n;
        	if((z+=t)>n)z-=n;
        	if((u+=t)>n)u-=n;
            /*x=(x+lastans)%n+1;
            y=(y+lastans)%n+1;
            z=(z+lastans)%n+1;
            u=(u+lastans)%n+1;*/
        }
    }
    void stop(){
        if(k>=2){write(res);putchar('\n');}
    }
}
long long ans;
int aid[N],bid[N];
int swp[N],sid[N],cnt[65536];
void sort(){
    //这里把base改成了256，不过好像区别不大
    cnt[0]=1;
    for(int i=1;i<256;i++)cnt[i]=0;
    for(int i=1;i<=n;i++)++cnt[a[i]&0xff];
    for(int i=1;i<256;i++)cnt[i]+=cnt[i-1];
    for(int i=n;i>=1;i--){
        swp[--cnt[a[i]&0xff]]=a[i];
        sid[cnt[a[i]&0xff]]=i;
    }

    cnt[0]=1;
    for(int i=1;i<256;i++)cnt[i]=0;
    for(int i=1;i<=n;i++)++cnt[(swp[i]>>8)&0xff];
    for(int i=1;i<256;i++)cnt[i]+=cnt[i-1];
    for(int i=n;i>=1;i--){
        a[--cnt[(swp[i]>>8)&0xff]]=swp[i];
        aid[cnt[(swp[i]>>8)&0xff]]=sid[i];
    }

	cnt[0]=1;
    for(int i=1;i<256;i++)cnt[i]=0;
    for(int i=1;i<=n;i++)++cnt[(a[i]>>16)&0xff];
    for(int i=1;i<256;i++)cnt[i]+=cnt[i-1];
    for(int i=n;i>=1;i--){
        swp[--cnt[(a[i]>>16)&0xff]]=a[i];
        sid[cnt[(a[i]>>16)&0xff]]=aid[i];
    }
    
    cnt[0]=1;
    for(int i=1;i<256;i++)cnt[i]=0;
    for(int i=1;i<=n;i++)++cnt[(swp[i]>>24)&0xff];
    for(int i=1;i<256;i++)cnt[i]+=cnt[i-1];
    for(int i=n;i>=1;i--){
        a[--cnt[(swp[i]>>24)&0xff]]=swp[i];
        aid[cnt[(swp[i]>>24)&0xff]]=sid[i];
    }
    
    cnt[0]=1;
    for(int i=1;i<256;i++)cnt[i]=0;
    for(int i=1;i<=n;i++)++cnt[b[i]&0xff];
    for(int i=1;i<256;i++)cnt[i]+=cnt[i-1];
    for(int i=n;i>=1;i--){
        swp[--cnt[b[i]&0xff]]=b[i];
        sid[cnt[b[i]&0xff]]=i;
    }

    cnt[0]=1;
    for(int i=1;i<256;i++)cnt[i]=0;
    for(int i=1;i<=n;i++)++cnt[(swp[i]>>8)&0xff];
    for(int i=1;i<256;i++)cnt[i]+=cnt[i-1];
    for(int i=n;i>=1;i--){
        b[--cnt[(swp[i]>>8)&0xff]]=swp[i];
        bid[cnt[(swp[i]>>8)&0xff]]=sid[i];
    }

	cnt[0]=1;
    for(int i=1;i<256;i++)cnt[i]=0;
    for(int i=1;i<=n;i++)++cnt[(b[i]>>16)&0xff];
    for(int i=1;i<256;i++)cnt[i]+=cnt[i-1];
    for(int i=n;i>=1;i--){
        swp[--cnt[(b[i]>>16)&0xff]]=b[i];
        sid[cnt[(b[i]>>16)&0xff]]=bid[i];
    }
    
    cnt[0]=1;
    for(int i=1;i<256;i++)cnt[i]=0;
    for(int i=1;i<=n;i++)++cnt[(swp[i]>>24)&0xff];
    for(int i=1;i<256;i++)cnt[i]+=cnt[i-1];
    for(int i=n;i>=1;i--){
        b[--cnt[(swp[i]>>24)&0xff]]=swp[i];
        bid[cnt[(swp[i]>>24)&0xff]]=sid[i];
    }

}
long long sum;
int cuta[N],cutb[N];
int prea[N],preb[N];
int pa[N],pb[N];
inline long long sol(int i,int j){
    if(a[i]>=b[j]){
        return cutb[j];
    }else{
        return ((cuta[i]-1LL*prea[i]*(preb[n]-preb[j]))%M+M)%M;
    }
}
int main(){
	//freopen("data.in","r",stdin);
	//freopen("data.out","w",stdout);
    lib::init();

    sort();
    for(int i=1;i<=n;i++){
        swp[i]=na[aid[i]];
    }
    for(int i=1;i<=n;i++){
        na[i]=swp[i];
    }
    sid[aid[1]]=1;
    for(int i=2;i<=n;i++){
        if(a[i]==a[i-1]){
            sid[aid[i]]=sid[aid[i-1]];
        }else{
            sid[aid[i]]=i;
        }
    }
    for(int i=1;i<=n;i++){
        aid[i]=sid[i];
    }
    for(int i=n-1;i>=1;i--){
        if(a[i]==a[i+1]){
            na[i]+=na[i+1];
            na[i]%=M;
            na[i+1]=0;
        }
    }
    for(int i=1;i<=n;i++)prea[i]=(prea[i-1]+na[i])%M;

    for(int i=1;i<=n;i++){
        swp[i]=nb[bid[i]];
    }
    for(int i=1;i<=n;i++){
        nb[i]=swp[i];
    }
    sid[bid[1]]=1;
    for(int i=2;i<=n;i++){
        if(b[i]==b[i-1]){
            sid[bid[i]]=sid[bid[i-1]];
        }else{
            sid[bid[i]]=i;
        }
    }
    for(int i=1;i<=n;i++){
        bid[i]=sid[i];
    }
    for(int i=n-1;i>=1;i--){
        if(b[i]==b[i+1]){
            nb[i]+=nb[i+1];
            nb[i]%=M;
            nb[i+1]=0;
        }
    }
    for(int i=1;i<=n;i++)preb[i]=(preb[i-1]+nb[i])%M;

    sum=0;
    for(int i=1;i<=n;i++){
        sum+=nb[i];
        sum%=M;
    }
    int j=1;
    for(int i=1;i<=n;i++){
        while(j<=n&&a[i]>=b[j]){
            sum-=nb[j];
            sum%=M;
            sum+=M;
            sum%=M;
            j++;
        }
        ans+=1LL*sum*na[i];
        ans%=M;
        pa[i]=j;
        cuta[i]=ans;
    }

    sum=0;
    ans=0;
    j=1;
    for(int i=1;i<=n;i++){
        while(j<=n&&b[i]>a[j]){
            sum+=na[j];
            sum%=M;
            j++;
        }
        ans+=1LL*sum*nb[i];
        ans%=M;
        pb[i]=j;
        cutb[i]=ans;
    }

    lib::reply(ans);

    for(int i=1;i<=q;i++){
        lib::query();

        x=aid[x];y=aid[y];
        if(a[x]>a[y]){u32 t=x;x=y;y=t;}
        z=bid[z];u=bid[u];
        if(b[z]>b[u]){u32 t=z;z=u;u=t;}
        x--;z--;

        ans=0;
        ans+=sol(y,u);
        ans-=sol(x,u);
        ans-=sol(y,z);
        ans+=sol(x,z);
        ans=(ans%M+M)%M;

        lib::reply(ans);
    }
    lib::stop();
}

~~这题别忘了IO模板的100多行~~

ID

4470

时间

3000ms

内存

500MiB

难度

标签

递交数

已通过

上传者

Hydro

1 条题解

自动搬运

以下是正文

算法1

算法2

算法3

算法4

算法5

算法6

关于 $O(1)$ 找位置

水晶

信息

1 条题解

自动搬运

以下是正文

算法1

算法2

算法3

算法4

算法5

算法6

关于O(1)O(1)O(1)找位置

水晶

信息

还没有账户？

登录

关于 $O(1)$ 找位置