自动搬运

查看原文

来自洛谷，原作者为

	yangrunze 蓝蓝的天空银河里，有只小白船

搬运于2025-08-24 22:09:29，当前版本为作者最后更新于2020-01-12 20:21:22，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

---

想必大家应该非常精通两种搜索算法——也就是深度优先搜索dfs和广度优先搜索bfs了，这时好奇的宝宝们也许会问啦：深度和广度到底还有什么意思呢？其实它们还有另外一层含义——图的遍历。

相信在座的各位应该知道图是个啥玩意，应该也知道“遍历”是啥：所谓“遍历”，就是把图上的每个顶点都找一遍呗！但是要找可不能瞎找，要不会把自己找晕，咱这里就有两种“防晕”的好方法！正所谓“举例是理解的试金石”，咱就拿样例来说！

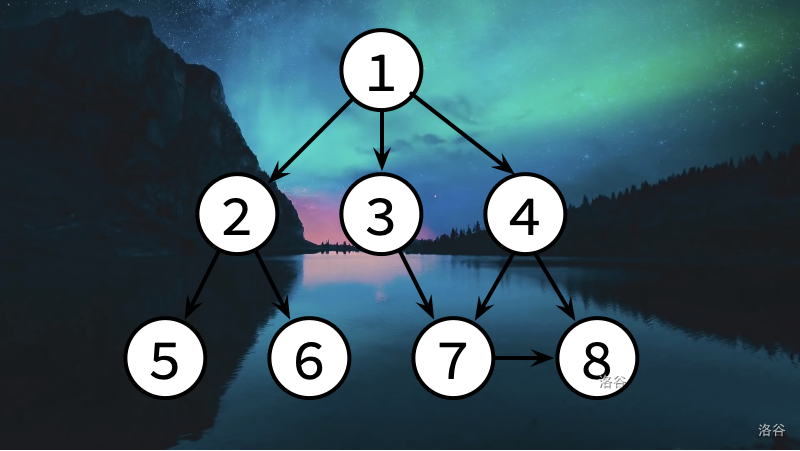
方法A

咱们可以一步一步向前去走：

从1出发，先去最小的2

然后从2出发，沿路到5

再从5出发......咦？没路了？好吧那就回去到2吧

出发点又到了2，这时候5已经到过啦，那就去6

6又没路了，好办！回到2，由于2通往的5和6都来过了，所以再回去到1，这时候1的路中2已经走过了，没走过的最前一个是3，那就在走到3

........

就这样一步一步走过去，可以得到顺序：

1 2 5 6 3 7 8 4

这种方法就是一步一步去尝试，先从一条路走到黑，走完了就回去找另一条，总结成7个字就是“不撞南墙不回头”，有没有发现跟我们的“深度优先搜索”迷之相似？？？所以，我们叫它“图的深度优先遍历”

方法B

想用这种方法，你需要掌握一项技能——分身术

还是从1出发，咱先把能走的都走一遍，依次到达2，3.4

1的走完了，咱就从下一个没往下走的地点开始，也就是从2出发，到达5，6

2的也走完了，目前最靠前的还没往下走过的点是3，好的，从3到达7，8

然后下一个没往下“扩展”的地点是4，哇，这时候7，8都已经走过了呢，那就走完啦

所以我们可以得到顺序：

1 2 3 4 5 6 7 8

总之就是把每个没有向下走过的地方都走一遍，如果你看懂了，你可以发现这个方法和“广度优先搜索”算法很像，我们就叫它“图的广度优先遍历”

---

两种遍历方法都讲完了，接下来咱们考虑的就只有细节问题了，首先，这个题数据范围那么大，用邻接矩阵存肯定是会爆的，那咱们就用一种新的方法。

首先，我们用一个结构体vector（为了节省空间，咱用vector来存）存储每个边的起点和终点，然后用一个二维vector（也就是一个vector数组）存储边的信息。

这个存储方法可能有点难理解，不过其实也没那么难：我们用$e$[$a$][$b$]=$c$，来表示顶点$a$的第$b$条边是$c$号边。咱举个栗子，还是拿样例说吧：

8 9
1 2 //0号边（由于vector的下标是从0开始的，咱就“入乡随俗”，从0开始）
1 3 //1号边
1 4 //2号边
2 5 //3号边
2 6 //4号边
3 7 //5号边
4 7 //6号边
4 8 //7号边
7 8 //8号边

最后二维vector中的存储会如下所示：

0 1 2 //1号顶点连着0、1、2号边
3 4	//2号顶点连着3、4号边
5	//3号顶点连着5号边
6 7 //4号顶点连着6、7号边
	//5号顶点没有边
	//6号顶点没有边
8	//7号顶点连着8号边
	//8号顶点没有边

看是不是对上号了？这个方法比较好懂，又节省空间，是个好方法。（此方法由大佬vectorwyx发明）

最后，别忘了题目要求：“如果有很多篇文章可以参阅，请先看编号较小的那篇”

那就排序呗！咱们按照题目要求，按照终点从小到大排列，如果终点相同按起点从小到大排列 注意我们说的第几号边是指排序后的序号

//准备工作：
struct edge{
	int u,v; //记录边的结构体，u起点，v终点
};
vector <int> e[100001];  //存具体信息的二维vector
vector <edge> s;  //存边的结构体vector数组
bool cmp(edge x,edge y){  //排序规则
	if(x.v==y.v)  //v相同按u排序
	return x.u<y.u;
	else return x.v<y.v;  //否则按v从大到小排序
}

//main函数里的内容	
	int n,m;  
	cin>>n>>m; //n个顶点，m条边，没啥好说的
	for(int i=0;i<m;i++){ //m条边
		int uu,vv;  
		cin>>uu>>vv;  
		s.push_back((edge){uu,vv}); //初始化存边的s数组  
	}
	sort(s.begin(),s.end(),cmp);
        //优雅地排个序（别忘了vector的操作：start返回第一个（指针）,end返回最后一个（指针））
	for(int i=0;i<m;i++)
		e[s[i].u].push_back(i); 
	//初始化e数组，在e[s[i].u]（也就是i号边的起点s[i].u连接的边的数组）中存入i号边

接下来就是遍历的过程，由于你们对两种搜素的过程那么熟悉，一定可以看懂下面的没有注释的代码！ （骗你们的，像我这么心地善良，怎么可能不给你们加注释）

bool vis1[100001]={0},vis2[100001]={0};
//vis数组用来判断有没有遍历过这个顶点，vis1用于深搜，vis2用于广搜（我才不会告诉你我懒得memset呢）

void dfs(int x){  //dfs——深度优先遍历，x表示当前遍历到x号顶点
	vis1[x]=1;  //这个顶点已经走过啦！
	cout<<x<<" "; //输出~
	for(int i=0;i<e[x].size();i++){ //一条一条边去搜索
		int point=s[e[x][i]].v;  //找出当前这条边（也就是e[x][i]）的终点
		if(!vis1[point]){   //如果这个点没走过
			dfs(point); //那就接着往下搜吧！
		}
	}
}

void bfs(int x){   //bfs——广度优先遍历（x依然是第几号顶点，不过既然不递归其实传这个参数也没啥用）
	queue <int> q;  //没有队列那还叫广搜吗
	q.push(x);  //先把第一个顶点推进去，输出，标记访问过
	cout<<x<<" ";  
	vis2[x]=1; 
	while(!q.empty()){   //广搜板子，上！
		int fro=q.front();  //把队首取出来
		for(int i=0;i<e[fro].size();i++){   //每条边去试
			int point=s[e[fro][i]].v;  //取终点（和dfs差不多）
			if(!vis2[point]){  //没访问过，推进去，输出，标记
				q.push(point); 
				cout<<point<<" ";
				vis2[point]=1;
			}
		}
		q.pop();  //队首搜完啦！把它弄出去
	}
}

这篇题解就到这里啦！Finally:AC code:

#include<iostream>  //头文件头文件头文件
#include<vector>
#include<queue>
#include<algorithm>
using namespace std;  
struct edge{       //存边结构体
	int u,v;
}; 
vector <int> e[100001];  //两个vector刚才已经详细讲过了
vector <edge> s;
bool vis1[100001]={0},vis2[100001]={0}; //标记数组
bool cmp(edge x,edge y){  //排序规则
	if(x.v==y.v)
	return x.u<y.u;
	else return x.v<y.v;
}
void dfs(int x){  //深度优先遍历
	vis1[x]=1;
	cout<<x<<" ";
	for(int i=0;i<e[x].size();i++){
		int point=s[e[x][i]].v;
		if(!vis1[point]){
			dfs(point);
		}
	}
}
void bfs(int x){  //广度优先遍历
	queue <int> q;
	q.push(x);
	cout<<x<<" ";
	vis2[x]=1;
	while(!q.empty()){
		int fro=q.front();
		for(int i=0;i<e[fro].size();i++){
			int point=s[e[fro][i]].v;
			if(!vis2[point]){
				q.push(point); 
				cout<<point<<" ";
				vis2[point]=1;
			}
		}
		q.pop();
	}
}
int main(){
	int n,m;  //输入，存边
	cin>>n>>m; 
	for(int i=0;i<m;i++){
		int uu,vv;
		cin>>uu>>vv;
		s.push_back((edge){uu,vv});   
	}
	sort(s.begin(),s.end(),cmp);  //排序
	for(int i=0;i<m;i++)   
		e[s[i].u].push_back(i); 
	dfs(1);   //从1号顶点开始深搜
	cout<<endl;
	bfs(1);   //广搜亦同理
}

The End~~~