自动搬运

查看原文

来自洛谷，原作者为

	fysbb That's♂good!

搬运于2025-08-24 22:06:17，当前版本为作者最后更新于2018-12-08 10:55:21，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

这里来说明一个时间复杂度为 $O(n \log n)$ 的算法，这个算法还能通过此题的加强版！双倍经验

显然 DFS 路径 $O(n)$ 的复杂度是无法优化的，所以具体要提高效率就得从断边入手。将原来的暴力，改为通过一次搜索来确定应该断的是哪条边。

如何找环，搜索路径，这里就不在赘述，我们具体分析如何断边：

比如这样的图

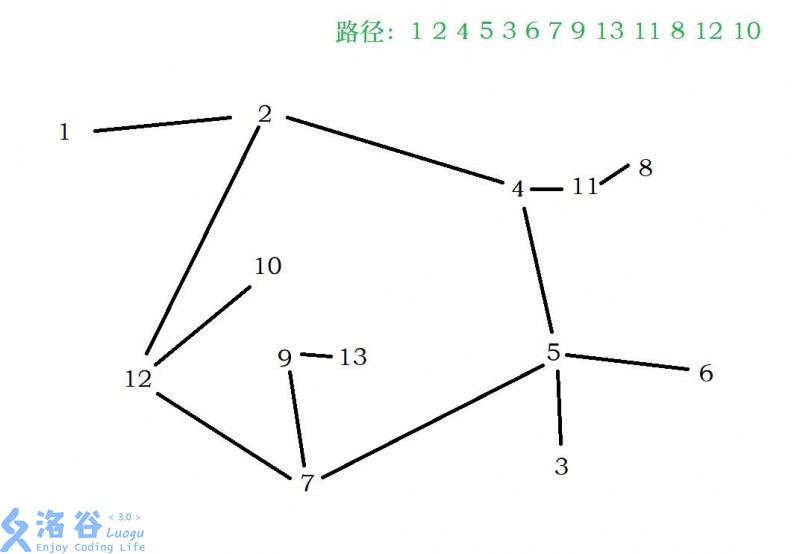
处理方法：

1.先找到环和环的入点（红色，橙色部分）

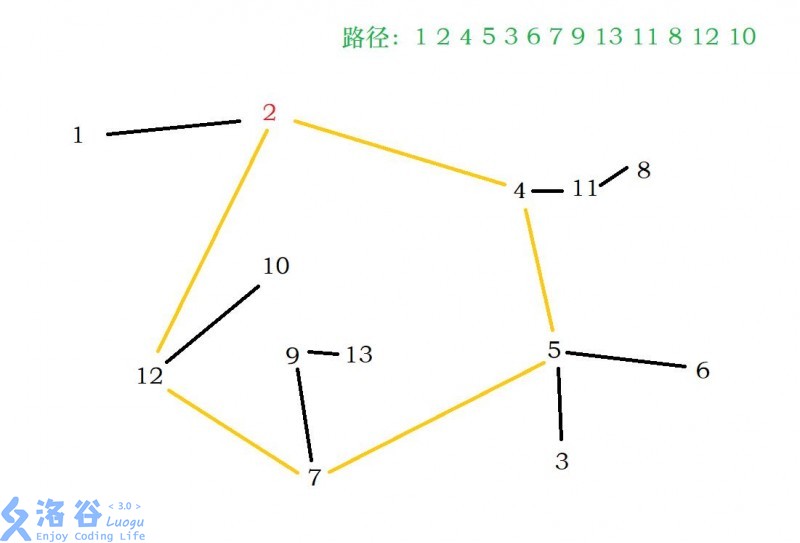
2.对环上的每个点预处理，找出其最大的子节点，入点不用处理（蓝色部分）

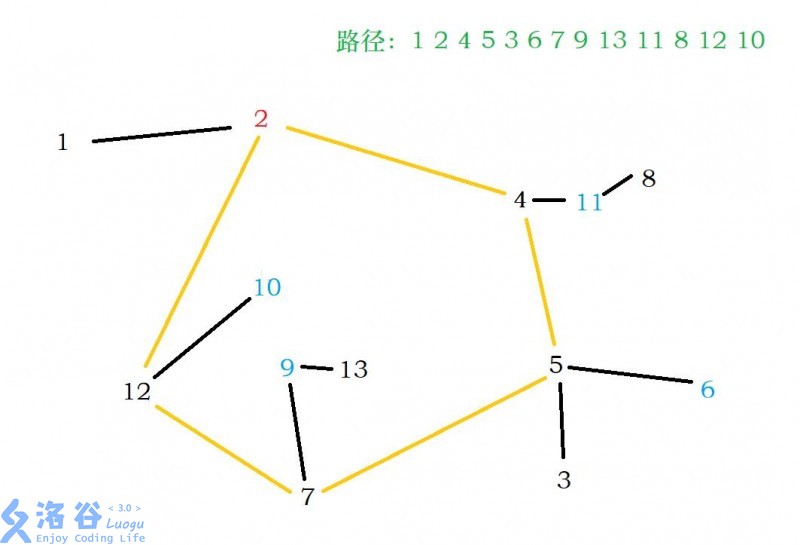
3.遍历整个环进行断边

设 $tmax[i]$ 为 $i$ 节点的最大子节点， $next[i]$ 为 $i$ 的后一个节点， $cut[i]$ 为 $i$ 的前一个有子节点的节点，该节点比 $i$ 大的子节点中最小的那一个子节点（此处所说的节点都为环上的节点，子节点都不是环上的节点）

first. 首先判断入点的两个叶节点，选择较小的进入环

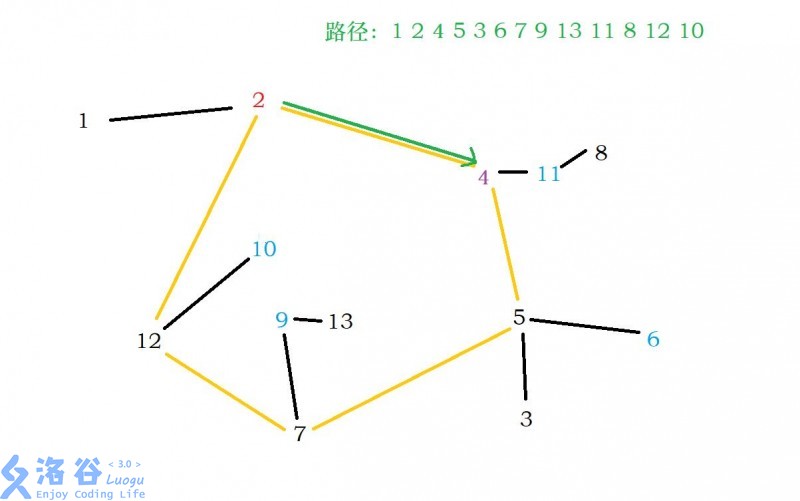
second. 若 $next[i] < tmax[i]$ ,则可以扩展到后一个节点

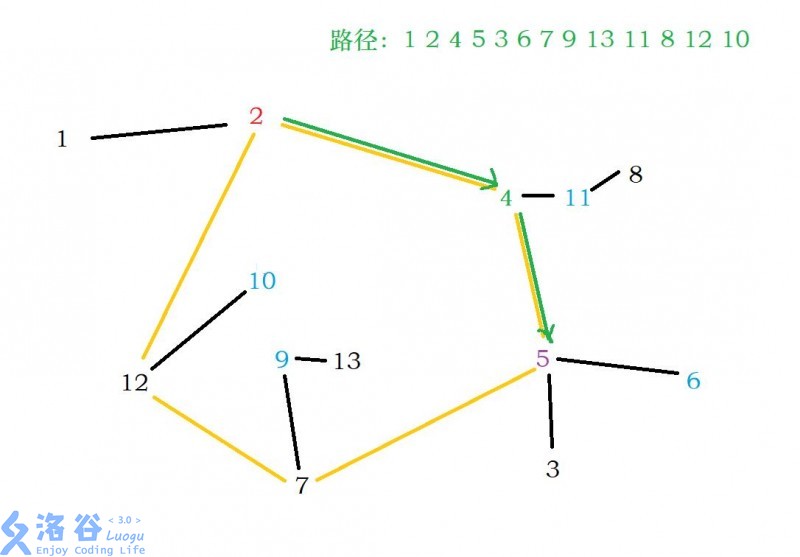
third. 若 $next[i] > tmax[i]$ 但是 $next[i] < cut[i]$ ,也可以扩展到后一个节点。

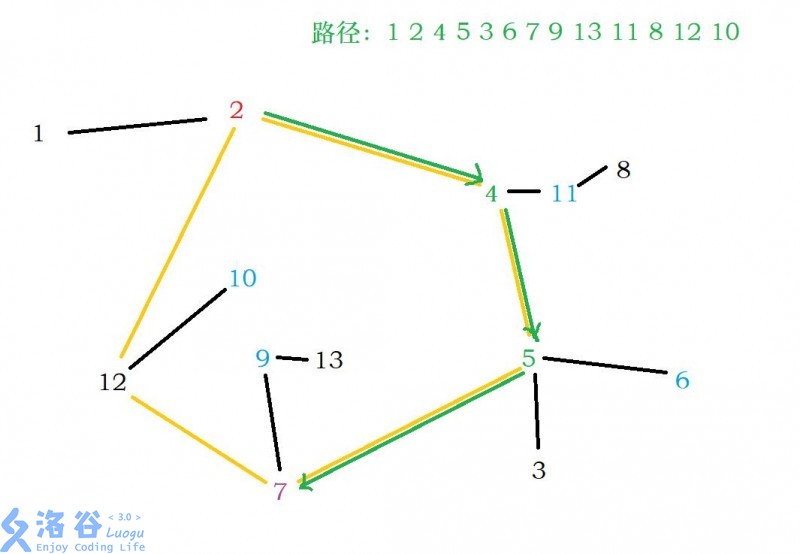
fourth. 若同时不满足second和third的条件，或 $next[i]$ 为入点，则不能继续扩展，并断开 $i$ 和 $next[i]$ 之间的边

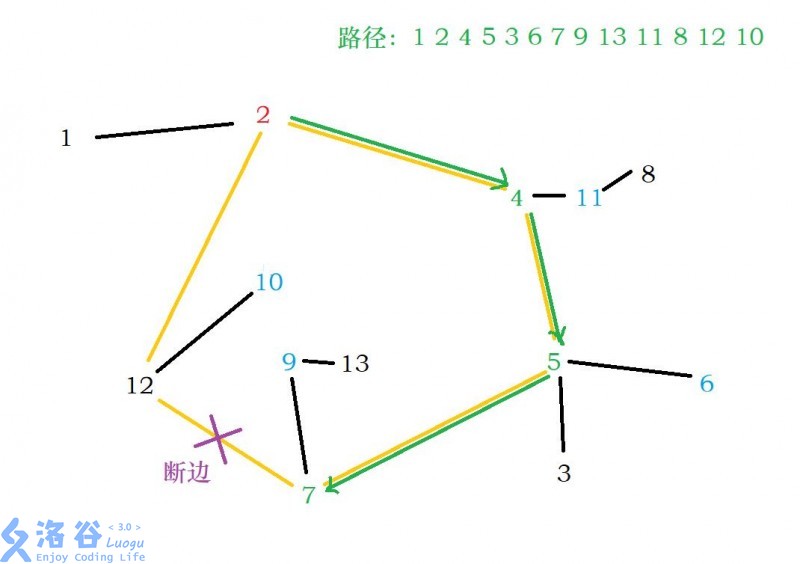
4. DFS搜索路径

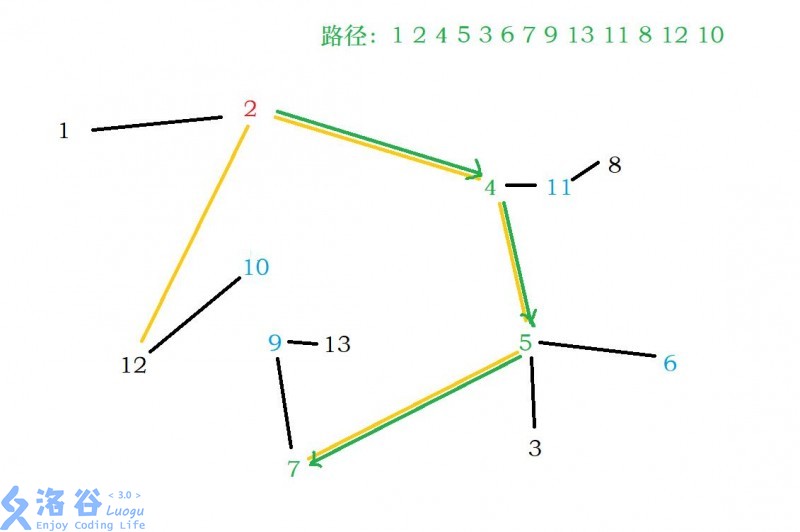
只要在断边后的图（一棵树）中用DFS搜索路径即可

5.时间复杂度

给边排序 $O(n \log n)$

找环 $O(n)$

断边 $O(n)$

搜索路径 $O(n)$

所以总时间复杂度接近 $O(n \log n)$ ，可以通过此体。

6.程序（pascal）

program project1;
var
   r,path,father,son,tmax:array[0..500005]of longint;
   ttf:array[0..500005]of boolean;
   l,v,x,y:array[0..1000005]of longint;
   n,m,p,k,fat,nox,noy:longint;

function max(a,b:longint):longint;
begin
  if a>b then exit(a) else exit(b);
end;

function min(a,b:longint):longint;
begin
  if a<b then exit(a) else exit(b);
end;

procedure sc(f,fa:longint);
var i:longint;
begin
  i:=r[f];
  while i<>0 do begin
    if (v[i]<>fa) and not((f=nox) and (v[i]=noy)) and not((f=noy) and (v[i]=nox)) then begin
      inc(k);
      path[k]:=v[i];
      sc(v[i],f);
    end;
    i:=l[i];
  end;
end;

function sc2(f,fa:longint):boolean;
var i:longint;
begin
  sc2:=false;
  i:=r[f];
  while i<>0 do begin
    if v[i]<>fa then begin
      if father[v[i]]=0 then father[v[i]]:=f
        else begin
          p:=v[i];
          fat:=father[v[i]];
          father[v[i]]:=f;
          son[f]:=v[i];
          exit(true);
        end;
      if sc2(v[i],f)=true then begin
        son[f]:=v[i];
        ttf[v[i]]:=true;
        exit(true)
      end;
    end;
    i:=l[i];
  end;
end;

procedure sc3;
var i,j:longint;
begin
  i:=p;
  while father[i]<>p do begin
    i:=father[i];
    j:=r[i];
    while j<>0 do begin
      if (v[j]<>son[i]) and (v[j]<>father[i]) then tmax[i]:=max(tmax[i],v[j]);
      j:=l[j];
    end;
  end;
end;

function mmax(k,p,o:longint):longint;
var i:longint;
begin
  mmax:=10000000;
  i:=r[p];
  while i<>0 do begin
    if (v[i]<>o) and (v[i]>k) then mmax:=min(mmax,v[i]);
    i:=l[i];
  end;
end;

function cut:longint;
var i,x,y,q,s:longint;
begin
  cut:=0;
  if father[p]<son[p] then begin
    i:=father[p];
    cut:=mmax(i,p,fat);
    while ((father[i]<tmax[i]) or ((father[i]>tmax[i]) and (father[i]<cut))) and (father[i]<>p) do begin
      i:=father[i];
      s:=mmax(i,son[i],son[son[i]]);
      if s<>10000000 then cut:=s;
    end;
    nox:=i;
    noy:=father[i];
  end else begin
    i:=son[p];
    cut:=mmax(i,p,fat);
    while ((son[i]<tmax[i]) or ((son[i]>tmax[i]) and (son[i]<cut))) and (son[i]<>p) do begin
      i:=son[i];
      s:=mmax(i,father[i],father[father[i]]);
      if s<>10000000 then cut:=s;
    end;
    nox:=i;
    noy:=son[i];
  end;
end;

procedure qsort(l,r:longint);
var i,j,mid,t:longint;
begin
  i:=l;
  j:=r;
  mid:=y[(i+j) div 2];
  repeat
    while y[i]>mid do inc(i);
    while y[j]<mid do dec(j);
    if i<=j then begin
      t:=y[i];
      y[i]:=y[j];
      y[j]:=t;
      t:=x[i];
      x[i]:=x[j];
      x[j]:=t;
      inc(i);
      dec(j);
    end;
  until i>j;
  if l<j then qsort(l,j);
  if i<r then qsort(i,r);
end;

procedure re;
var i,t,xx,yy:longint;
begin
  for i:=1 to m do begin
    read(xx,yy);
    t:=2*i;
    x[t]:=xx;
    y[t]:=yy;
    x[t-1]:=yy;
    y[t-1]:=xx;
  end;
  qsort(1,2*m);
  for i:=1 to 2*m do begin
    l[i]:=r[x[i]];
    r[x[i]]:=i;
    v[i]:=y[i];
  end;
end;

procedure main;
var i:longint;
begin
  k:=0;
  inc(k);
  path[k]:=1;
  father[1]:=1;
  if m=n then begin
    sc2(1,0);
    sc3;
    cut;
  end;
  sc(1,0);
  for i:=1 to k do write(path[i],' ');  writeln;
end;

begin
  fillchar(r,sizeof(r),0);
  fillchar(l,sizeof(l),0);
  read(n,m);
  re;
  main;
end.