自动搬运

查看原文

来自洛谷，原作者为

	TimeTraveller Travel in the Time

搬运于2025-08-24 22:05:54，当前版本为作者最后更新于2018-11-06 09:07:58，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

这个题其实是个大模拟（逃

Ps. 这里的$n$为题中的$n$加上开始平台的长度再加2。

数据有两个是样例，数据太难造了，QWQ

为什么那么多人只输出了样例QAQ

算法1

我们直接深搜模拟，选取前$k$大的加到答案即可。

• 复杂度：$O(n!+(n!)log(n!)+k)$
• 期望得分：$20$

算法2

我们$n^3$暴力将发射与集中的关系建有向图，可以发现，环是不能走多次的，所以是个DAG（有向无环图），然后在上面搜一遍，取前$k$大的加入答案即可。

• 复杂度：$O(n^3+n^2+nlogn+k)$
• 期望得分：$30\sim 60$

算法3

我们发现建图时，每个点只会连出去最多两条，所以我们将平台按照$y$的大小排序，然后$n^2$的就可以建完图了，同样的搜一遍，取前$k$大的加入答案即可。

• 复杂度：$O(n^2+nlogn+k)$
• 期望得分：$70$

算法4

我们发现，$DP$时，对于已经在之前搜过的状态，是不会变的，所以用类似记忆化搜索的方法，可以将搜索的复杂度将为$n$。

• 复杂度（因为建图的$n^2$还没解决）：$O(n^2+nlogn+k)$
• 期望得分:$70\sim 80$

算法5

我们可以将每个平台拆为若干点，然后对平台按照$y$和$x$排序后直接用直线函数求交点，直接建图，当每个平台（除了开始平台和飞船）建边超过2条时（这两条要合法），就不用再建了。

类似下图,1234为一个平台，56为一个，78为一个。

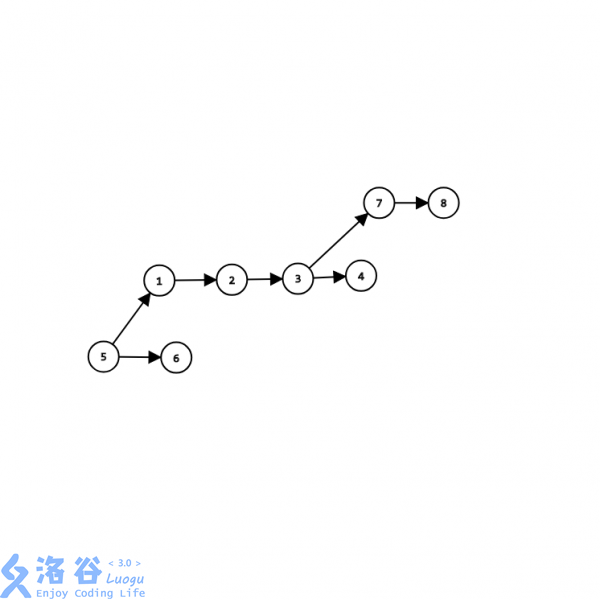
建图的复杂度为$\sum\text{平台长度}\sim (\sum\text{平台长度})^2$,但是最坏是达不到的。

• 期望复杂度：$O(\sum\text{平台长度}+nlogn+k)$
• 期望得分：$80\sim 90$

算法6

有的点太多了，所以要将其缩为一个点，所以将其他平台全部看成一个点。

我们发现只有两种边，一种为北偏东$45^{\circ}$，一种为南偏东$45^{\circ}$，其实最后建出来的边只有最多$2n$条。

所以我们使用扫描线和平衡树辅助建边，将复杂度降为$nlogn$。

扫描线，这里可不是平行于$x$或者$y$轴扫，因为是斜的，所以我们在$y=x$和$y=-x$两个方向上扫两次，可以分别按照第一关键字为$x+y$和$x-y$第二关键字为$y$对点排序，而平衡树用$y$为第一关键字$x+y$和$x-y$为第二关键字。

然后将一个平台拆成入点出点和发射点，三个点。

开始平台则拆为$x2-x1+1$个点，飞船拆为两个点。

然后对点排序，做两次扫描线建图，使用记忆化搜索即可拿到全部的分。

这里的平衡树可以用$STL$中的$set$实现。

• 复杂度$O(nlogn+k)$
• 期望得分$100$

下面为code（不要copy，可能不对）：

#include<set>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#define ll long long
using namespace std;
const int M=4e6+10;
int n,m,x1,x2,K,yy,wx,sy,ty;；
ll vall[M],V;
int lstot,CMP；
struct point{
    int x,y,id,type,upd;
    point(){}
    point(int x,int y,int id,int type,int upd)
    :x(x),y(y),id(id),type(type),upd(upd){}
    bool operator <(const point &a)const{
        if(CMP){
            return y<a.y||((y==a.y)&&(x-y)<(a.x-a.y));
        }else{
            return y>a.y||((y==a.y)&&(x+y)<(a.x+a.y));
        }
    }
}pp[M]；
bool isin[M];
multiset <point> S;
typedef multiset<point>::iterator iter;
struct Line{
    int type,xl,xr,y,pos,w,upd;
    Line(){}
    Line(int a,int b,int c,int d,int e,int f,int g)
    :type(a),xl(b),xr(c),y(d),w(e),upd(f),pos(g){}
    void in(int i){
        scanf("%d%d%d%d",&type,&xl,&xr,&y);
        pp[++lstot]=point(xl,y,i,1,-1);
        pp[++lstot]=point(xr,y,i,-1,-1);
        if(type==1){
            scanf("%d%d%d",&pos,&w,&upd);
            vall[i]=w;
            pp[++lstot]=point(pos,y,i,0,upd);
        }else if(type==2){
            scanf("%d%d",&pos,&w);
            vall[i]=w;
            pp[++lstot]=point(pos,y,i,0,2);
        }
    }
}L;
bool cmp1(const point &a,const point &b){
    if((a.x-a.y)==(b.x-b.y)){
        if(a.y==b.y){
            return a.type>b.type;
        }else if(a.type!=b.type){
            return a.type>b.type;
        }else{
            return a.y>b.y;
        }
    }else return (a.x-a.y)<(b.x-b.y);
}
bool cmp2(const point &a,const point &b){
    if((a.x+a.y)==(b.x+b.y)){
        if(a.y==b.y){
            return a.type>b.type;
        }else if(a.type!=b.type){
            return a.type>b.type;
        }else{
            return a.y<b.y;
        }
    }else return (a.x+a.y)<(b.x+b.y);
}
int ed;
ll rec[M],inf,anss[M],cct[M];
struct ss{
    int to,last;
    ss(){}
    ss(int a,int b):to(a),last(b){}
}g[M<<2];
int head[M],cnt;
int dfn[M],top;bool in[M];
void add(int a,int b){g[++cnt]=ss(b,head[a]);head[a]=cnt;}
ll dfs(int a,ll v){
    if(a==ed) return cct[ed]=1,rec[ed]=0,0;
    ll val=0,ans=0;in[a]=1;
    for(int i=head[a];i;i=g[i].last){
        if(rec[g[i].to]!=inf){
            val+=cct[g[i].to]*vall[a]+rec[g[i].to];
        }else if(!in[g[i].to]){
            ll to=dfs(g[i].to,v+vall[a]);
            val+=cct[g[i].to]*vall[a]+rec[g[i].to];
        }
        cct[a]+=cct[g[i].to];
    }
    in[a]=0;
    rec[a]=val;
    return v*cct[a]+val;
}
void Init_1(){
    int nowtot=n;
    for(int i=x1;i<=x2;i++){
        ++nowtot;
        pp[++lstot]=point(i,yy,nowtot,0,0);
        vall[nowtot]=V;
    }
    ++nowtot;ed=nowtot;
    pp[++lstot]=point(wx,sy,nowtot,-1,1);pp[++lstot]=point(wx,ty,nowtot,1,-1);
}
void tu(point a){
    S.insert(a);
    iter p=S.find(a);
    if(p!=S.begin()){
        for(--p;;--p){
            point t=*p;
            if(isin[t.id]&&t.id!=a.id){
                add(a.id,t.id);break;
            }else if(!isin[t.id]){
                S.erase(p);
                p=S.find(a);
            }
            if(p==S.begin()) break;
        }
    }
}
void UP(point a){
    if(a.type==1){
        S.insert(a);
        isin[a.id]=1;
    }else if(a.type==0){
        if(a.upd==2||a.upd==0)tu(a);
    }else if(a.type==-1){
        isin[a.id]=0;
    }
}
void DOWN(point a){
    if(a.type==1){
        S.insert(a);
        isin[a.id]=1;
    }else if(a.type==0){
        if(a.upd==2||a.upd==1) tu(a);
    }else if(a.type==-1){
        isin[a.id]=0;
    }
}
void workup(){
    sort(pp+1,pp+lstot+1,cmp1);
    int now;
    for(int i=1;i<=lstot;){
        now=pp[i].x-pp[i].y;
        UP(pp[i]);
        ++i;
        while(i<=lstot&&pp[i].x-pp[i].y==now)UP(pp[i++]);
    }
}
void workdown(){
    sort(pp+1,pp+lstot+1,cmp2);
    int now;
    for(int i=1;i<=lstot;){
        now=pp[i].x+pp[i].y;
        DOWN(pp[i]);
        ++i;
        while(i<=lstot&&pp[i].x+pp[i].y==now)DOWN(pp[i++]);
    }
}
void Init_2(){
    workup();
    CMP=1;
    memset(isin,0,sizeof(isin));
    for(int i=1;i<=lstot;i++){
        if(pp[i].id==ed){
            if(pp[i].type==-1) pp[i].type=1;
            else if(pp[i].type==1) pp[i].type=-1;
        }
    }
    workdown();
}
void Read(){
    memset(rec,0x3f,sizeof(rec));inf=rec[0];
    scanf("%d%d",&K,&n);
    scanf("%d%d%d%lld",&x1,&x2,&yy,&V);
    scanf("%d%d%d",&wx,&sy,&ty);
    for(int i=1;i<=n;i++)L.in(i);
}
void Init(){Init_1();Init_2();}
bool cmp3(ll a,ll b){return a>b;}
void Work(){
    int tot=0;ll ans=0;
    for(int i=x1;i<=x2;i++)anss[++tot]=dfs(n+i-x1+1,0);
    sort(anss+1,anss+tot+1,cmp3);
    for(int i=1,up=min(tot,K);i<=up;i++)ans+=anss[i];
    printf("%lld\n",ans);
}
int main(){
    Read();
    Init();
    Work();
    return 0;
}