自动搬运

查看原文

来自洛谷，原作者为

	ZAGER **

搬运于2025-08-24 22:03:44，当前版本为作者最后更新于2018-10-21 21:57:12，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

题解

透彻

首先看数据范围

1. 1-4组数据$N\leq20$，爆搜就可以解决。

   inline void dfs(R ll dep,R ll sum){
      if(sum>m)return;
      if(dep==n+1){
          ans++;
          return;
      }
      dfs(dep+1,sum+a[dep]);
      dfs(dep+1,sum);
   }
   int main(){
      read(n);read(m);
      for(R int i=1;i<=n;i++)read(a[i]);
      if(n<=20){
          dfs(1,0);
          printf("%lld\n",ans);
      }
      return 0;
   }
   

2. 5-7组数据$M\leq10^6$，裸的背包啊。

   int main(){
   	read(n);read(m);
   	for(R int i=1;i<=n;i++)read(a[i]);
       if(m<=1e6){
           f[0]=1;
           for(R int i=1;i<=n;i++)
               for(R int j=m;j>=a[i];j--)
                   f[j]+=f[j-a[i]];
           for(R int i=0;i<=m;i++)ans+=f[i];
           printf("%lld\n",ans);
       }
       return 0;
   }
   
   

3. 现在你已经能拿到70分了（但在洛谷上是47分）

下面引出主角——折半搜索（meet in the middle思想）

因为$N\leq40$ $O(2^{40})$的爆搜一定会$TLE$，所以我们将$N$分成两份

搜索$1$到$n/2$和$n/2+1$到$n$，让复杂度降到$O(2^{n/2+1}+$组合答案的复杂度$)$。

画一个图（网上找的不错的图）理解一下为什么能降低复杂度

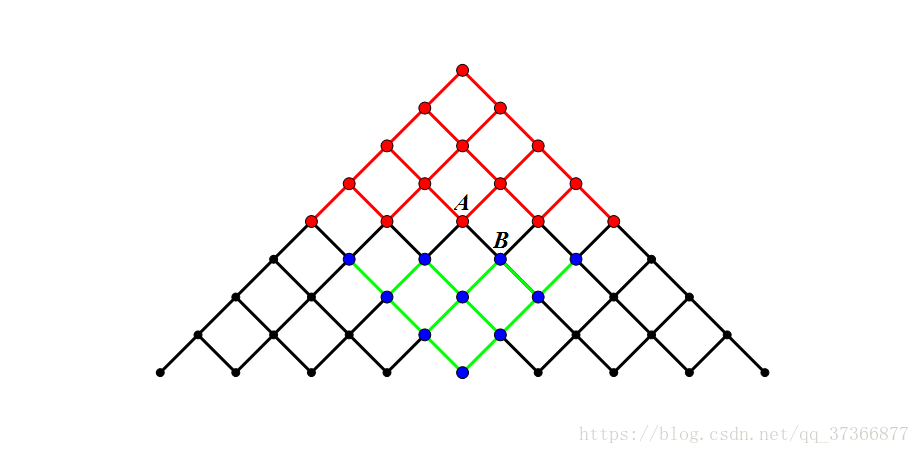
inline void dfs(R int l,R int r,R ll sum,R ll a[],R ll &cnt){
    if(sum>m)return;
    if(l>r){
        a[++cnt]=sum;
        return;
    }
    dfs(l+1,r,sum+w[l],a,cnt);//选
    dfs(l+1,r,sum,a,cnt);//不选
}

将前一半的搜索状态存入a数组，后一半存入b数组。

mid=n/2;
dfs(1,mid,0,suma,cnta);
dfs(mid+1,n,0,sumb,cntb);

一般$meet$ $in$ $the$ $middle$的难点主要在于最后答案的组合统计。

我们可以现将a或b数组sort，让其有序。

然后通过枚举另一个数组中的状态，来实现统计答案。

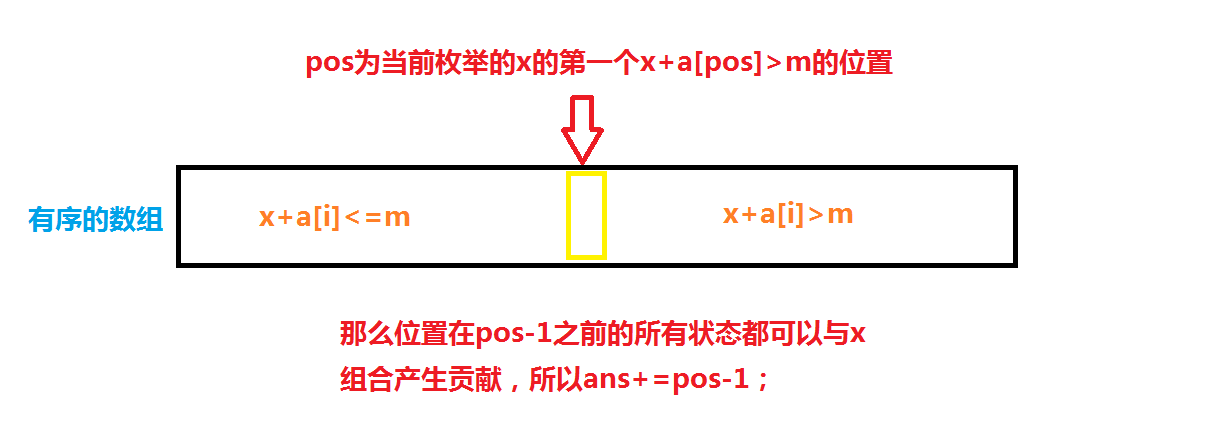
上述找$pos$的过程可以通过upper_bound()完成。

sort(suma+1,suma+1+cnta);//使一个数组有序
for(R int i=1;i<=cntb;i++)
    ans+=upper_bound(suma+1,suma+1+cnta,m-sumb[i])-suma-1;//统计ans

下面是高清完整code：

#include<iostream>
#include<algorithm>
#include<cstdio>
#include<cstring>
#include<cctype>
#define ll long long
#define R register
#define N 55
using namespace std;
template<typename T>inline void read(T &a){
    char c=getchar();T x=0,f=1;
    while(!isdigit(c)){if(c=='-')f=-1;c=getchar();}
    while(isdigit(c)){x=(x<<1)+(x<<3)+c-'0';c=getchar();}
    a=f*x;
}
ll n,m,w[N],mid,suma[1<<21],sumb[1<<21],cnta,cntb,ans;
inline void dfs(R int l,R int r,R ll sum,R ll a[],R ll &cnt){
    if(sum>m)return;
    if(l>r){
        a[++cnt]=sum;
        return;
    }
    dfs(l+1,r,sum+w[l],a,cnt);
    dfs(l+1,r,sum,a,cnt);
}
int main(){
    read(n);read(m);
    for(R int i=1;i<=n;i++)read(w[i]);
    mid=n>>1;
    dfs(1,mid,0,suma,cnta);
    dfs(mid+1,n,0,sumb,cntb);
    sort(suma+1,suma+1+cnta);
    for(R int i=1;i<=cntb;i++)
        ans+=upper_bound(suma+1,suma+1+cnta,m-sumb[i])-suma-1;
    printf("%lld\n",ans);
    return 0;
}

这里还有一道折半搜索的好题，难度升级——luogu，还有 my blog.