自动搬运

查看原文

来自洛谷，原作者为

	LittleDino 喵

搬运于2025-08-24 22:03:26，当前版本为作者最后更新于2019-06-03 23:24:52，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

---

感谢给我讲了这个题的神仙跳瓜 $\textrm{jumpmelon}$。

首先看给的提示，我们可以发现在这样的排序方式下，对于每一个数都只向目标位置方向走，不换向。那么对于一个数 $x$，如果有一个比它大的数在它前面，那么它必须向左走；如果有一个比它小的数在它后面，那么它必须向右走。这样的排列是不合法的，即要求不存在长度超过 $2$ 的下降子序列。

根据 $\textrm{Dilworth}$ 定理，最长下降子序列的长度不超过 $2$，即整个排列最多被划分成 $2$ 个上升子序列。

先不考虑字典序严格大于 $q$ 的限制。

我们记 $f_{i, j}$ 为前 $i$ 个的最大值为 $j$ 后面 $n - i$ 个位置的方案数。我们考虑第 $i$ 个数填什么。注意 $i \leqslant j$

如果填比 $j$ 大的数，那么一定可以接在 $j$ 的后面；如果要填比 $j$ 小的数，那么必须填当前还没有填的中最小的，否则上升子序列将不止 $2$ 个，所以

$$\begin{aligned} f_{i, j} &= \begin{cases} f_{i + 1, k} \ \ \ \ \ (k > j) \\ f_{i + 1, j} \ \ \ \ \ \end{cases} \\ &= \sum_{k = j}^n f_{i + 1, k} \end{aligned} $$

但是直接这样递推是 $O(n^2)$ 的。我们把它以图像的形式表示，$f_{i, j}$ 即表示从点 $(i, j)$ 开始，每次向右走一步，向上走 $x(x \leqslant 0)$ 步，不与直线 $y = x - 1$ （因为 $i \leqslant j$） 相交，走到点 $(n, n)$ 的方案数。

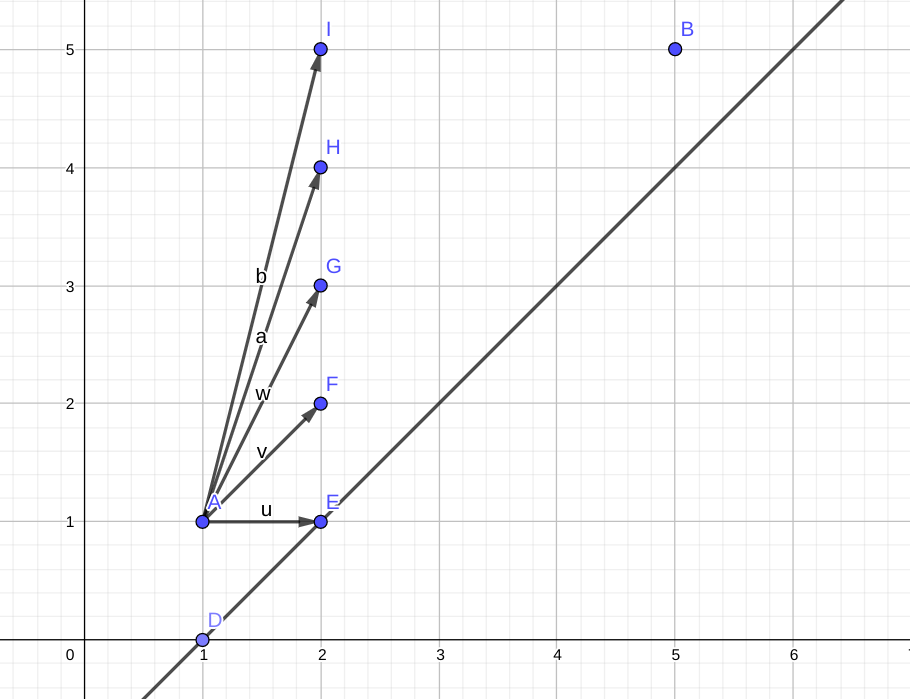
如图，即从点 $A(i, j)$ 走到 $B(n, n)$ 的不与直线 $y = x - 1$ 相交的方案数。

首先，如果不考虑与直线不相交，即为走 $n - i$ 次，每次选择向上走 $x (x \geqslant 0)$ 步，一共走了 $n - j$ 步的方案数。模仿插板法，因为 $x$ 可以取 $0$，我们把总个数加上划分数 $n - i$，变成 $n - i + n - j$ 个物品划分成 $n - i$ 块的方案数，即 $\dbinom{2n - i - j - 1}{n-i-1}$。

再模仿 $\textrm{Catalan}$ 数的推法，看第一个与直线 $y = x - 1$ 相交的位置。找点 $(i, j)$ 关于直线 $y = x - 1$ 的对称点 $(j + 1, i - 1)$, 由于方案一一对应，所以，从点 $(i, j)$ 出发，经过直线的方案数即为从点 $(j + 1, i - 1)$ 出发到点 $(n, n)$ 的方案数。

得到

$$\begin{aligned} f_{i, j} &= calc(i, j) - calc(j + 1, i - 1) \\ &= \dbinom{2n - i - j - 1}{n - i - 1} - \dbinom{2n - i - j - 1}{n - j - 2} \\ \end{aligned} $$

这样就得到 $f$ 的 $O(1)$ 求解啦！（然而 $O(n^2)$ 有足足 $80$ 分，真香)

可以发现 $f_{0, 0}$ 即为 $\textrm{Catalan}$ 数，可以得到 $12$ 分。

回到有限制字典序严格大于 $q$ 的原题上来。考虑一位一位枚举，假设当前枚举到第 $i$ 项，我们计数证前 $i - 1$ 项与 $q$ 相同，第 $i$ 项大于 $q_i$ 的排列个数。

记 $mx = \max_{j = 1}^{i - 1} q_j$，$mn$ 为当前还没有用过的最小的数，$v = q_i$。第 $i$ 位只能填 $mn$ 或大于 $mx$ 的数。分类讨论

• $v = mn$

  （因为 $mn$ 是最小可以填的，所以 $v$ 的下界是 $mn$。）

  此时，第 $i$ 项不能填 $mn$，只能大于 $mx$，故后面 $n - i$ 项的填法有 $\sum_{k = mx + 1}^n f_{i, k}$ 种（$k$ 为第 $i$ 位填的数）。

• $mn < v < mx$

  此时第 $i$ 位没有可以填的，后面不再存在合法方案。（但是还是要读完）

• $v \geqslant mx$

  此时第 $i$ 位可以填 $mn$ 或大于 $mx$ 的数，方案数为 $\sum_{k = mx}^n f_{i, k}$。

问题又来了，怎么求 $f$ 的前缀和呢？考虑 $f$ 的递推式 $f_{i, j} = \sum_{k = j}^n f_{i + 1, k}$，这正是一个前缀和的形式。所以

$$\sum_{k = lim}^n f_{i, k} = f_{i - 1, lim}$$

不用像其他题解上说的要用树状数组，复杂度 $O(Tn)$（还好写)

完结撒花~

代码

注意数组要开 $2n$，写起来很简单，但是最开始由于没彻底搞懂想了半天

#include <bits/stdc++.h>
using namespace std;

namespace TYC
{
    typedef long long ll;
    const int N = 1.2e6, p = 998244353;

    int fac[N + 5], inv[N + 5], vis[N + 5];

    inline int read()
    {
        int v = 0, fl = 0, ch = getchar();
        while (!isdigit(ch))
            fl |= (ch == '-'), ch = getchar();
        while (isdigit(ch))
            v = v * 10 + ch - '0', ch = getchar();
        return fl ? -v : v;
    }

    inline int qpow(int v, int tim)
    {
        int ans = 1;
        for (; tim; tim >>= 1, v = (ll)v * v % p)
            if (tim & 1)
                ans = (ll)ans * v % p;
        return ans;
    }

    void init()
    {
        fac[0] = 1;
        for (int i = 1; i <= N; i++)
            fac[i] = (ll)fac[i - 1] * i % p;
        inv[N] = qpow(fac[N], p - 2);
        for (int i = N; i; i--)
            inv[i - 1] = (ll)inv[i] * i % p;
    }

    inline int C(const int n, const int m)
    {
        return (n < 0 || m < 0 || n < m) ? 0 : int((ll)fac[n] * inv[m] % p * inv[n - m] % p);
    }

    int n;
    inline int F(const int i, const int j)
    {
        return i <= j && j <= n ? (C(2 * n - i - j - 1, n - i - 1) - C(2 * n - i - j - 1, n - j - 2) + p) % p : 0;
    }

    void work()
    {
        init();
        int T = read();
        while (T--)
        {
            n = read();
            memset(vis, 0, sizeof(int[n + 1]));
            int ans = 0, mx = 0, mn = 1, flag = 0, v;
            for (int i = 1; i <= n; i++)
            {
                v = read();
                if (flag)
                    continue;
                ans = (ans + (F(i - 1, max(mx, v) + 1) + p) % p) % p;
                if (mx > v && v > mn)
                    flag = 1;
                mx = max(mx, v);
                vis[v] = 1;
                while (vis[mn]) mn++;
            }
            printf("%d\n", ans);
        }
    }
}

int main()
{
    TYC::work();
    return 0;
}

P.S.
upd 2023.8.5 我已经退役很多年了，一次碰巧上洛谷看到有同学提醒组合数写反了，现特为纠正，希望同学们都能看明白。