自动搬运

查看原文

来自洛谷，原作者为

	FlierKing **

搬运于2025-08-24 22:03:17，当前版本为作者最后更新于2018-07-14 23:34:55，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

考虑最大的$f(i,j)=| \sum_{p=i}^j a_p |$本质是什么

换为前缀和的形式 $f(i,j)=|pre_j - pre_i|$

将绝对值拆掉 $$f(i,j)=\left{\begin{matrix} pre_j-pre_i & if\ pre_{j}>pre_{i}\ pre_i-pre_j & if\ pre_{j} \le pre_{i} \end{matrix}\right.$$

所以$\max_{1 \le i \le j \le n} f(i,j)$

$=\max pre_i - \min pre_j$

如果给整个数组加上 $x$，那么 $pre'_i=pre_i+ix$

那么当我们确定了整个数组加上的数字$x$，我们就能确定每个位置的前缀和，考虑如何求出最大的前缀和和最小的前缀和。

这个是个一次函数的形式，我们可以将前面的 $n+1$ 个一次函数加入坐标系，维护一个下凸包表示整个数组加上$x$时最大的前缀和，维护一个上凸包表示最小的前缀和。

这个是样例的图，其中紫色的为5条一次函数，黄色的为下凸包，红色的为下凸包。那么当我们要求整个数组加上$h$的答案时，$x$坐标为$h$的下凸包的$y$坐标减去$x$坐标为$h$的上凸包的$y$坐标得到的差即为询问的答案。

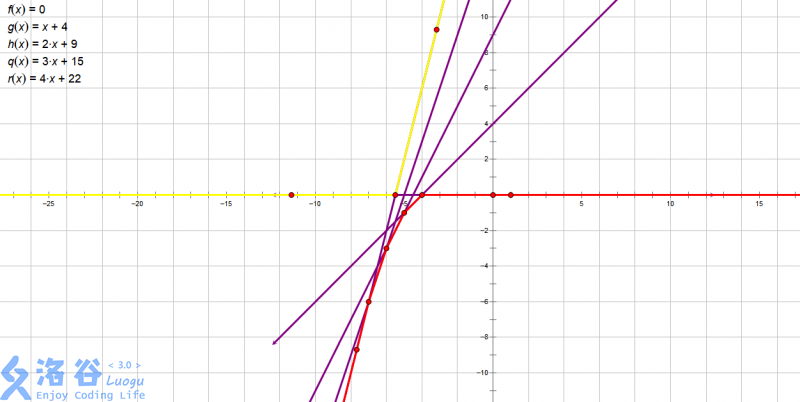
那么我们维护凸包，记下凸包上每条线段两端的位置后，我们可以二分横坐标$h$是在哪个线段上，求出相应的$y$值。

最后上凸包的值-下凸包的值即为答案。

时间复杂度为$O(n\ log\ n)$

#include <bits/stdc++.h>
#define MN 200005
#define ll long long
using namespace std; 
    int n,m,l,r,mid,a,b,x;
    ll s[MN],mx[MN],mxn,mn[MN],mnn,pre;
    double mxp[MN],mnp[MN];
inline int read()
{
    int x=0,f=1;char c;
    while((c=getchar())<'0'||c>'9')if(c=='-')f=-1;
    for(;c>='0'&&c<='9';c=getchar())x=x*10+c-'0';
    return x*f;
}
inline double cal(int a,int b){return double(s[b]-s[a])/(a-b);}
int main()
{
    n=read();m=read();
    for(int i=1;i<=n;i++)
    {
        s[i]=s[i-1]+read();
        while(mxn&&cal(i,mx[mxn])<=cal(i,mx[mxn-1]))--mxn;mx[++mxn]=i;
        while(mnn&&cal(i,mn[mnn])>=cal(i,mn[mnn-1]))--mnn;mn[++mnn]=i;
    }
    for(int i=1;i<=mxn;i++)mxp[i]=cal(mx[i],mx[i-1]);
    for(int i=1;i<=mnn;i++)mnp[i]=cal(mn[i],mn[i-1]);
    while(m--)
    {
        x=(read()+pre)%(4*n+1)-2*n;
        if(x<=mxp[1])a=0;
        else for(l=1,r=mxn;l<=r;)
        {
            mid=(l+r)>>1;         
            if(x>=mxp[mid])a=mx[mid],l=mid+1;
            else r=mid-1;
        }
        if(x>=mnp[1])b=0;
        else for(l=1,r=mnn;l<=r;)
        {
            mid=(l+r)>>1;
            if(x<=mnp[mid])b=mn[mid],l=mid+1;
            else r=mid-1;
        }
        printf("%lld\n",pre=(ll)(a-b)*x+s[a]-s[b]);
    }
    return 0;
}