1 条题解
-
0
自动搬运
来自洛谷,原作者为

御·Dragon
退役选手。联系请进Blog搬运于
2025-08-24 21:55:37,当前版本为作者最后更新于2019-06-01 15:46:55,作者可能在搬运后再次修改,您可在原文处查看最新版自动搬运只会搬运当前题目点赞数最高的题解,您可前往洛谷题解查看更多
以下是正文
年 月 日更博报告:
1 月的更新虽然完善了一些问题,但是讲得比较快,有些同学看不大懂,故再次更新,还有什么不懂的请私信我。
由于各种问题,使得原本在博客园中排版精美的源码在这里丑陋不堪。故更好的阅读效果请点击这里
年 月 日更博报告:
士别三日,刮目相待。更新一些细节的描述,优化排版。希望这篇题解能够帮助更多初学者,成为最好的题解。
年 月 日更博报告:
有同学反应图萎掉了,
我穷所以图床效果一般,请等待一下图片将会出现哈~
文字讲解
题目分析:
首先 ,要知道这道题是 拓扑排序。不妨先从拓扑排序定义下手,分析题目的性质。经分析得:
食物链中的生物 —— 节点
生物之间的关系 —— 有向边
为了方便描述,我们将
不会捕食其他生物的 生产者 叫做 最佳生产者
不会被其他生物捕食的 消费者 叫做 最佳消费者
由于数据中不会出现环,所以 最大食物链 即 左端是 最佳生产者 ,右端是 最佳消费者 的路径
而 只要最左端是 最佳生产者 的路径(即最右端可以不是 最佳消费者 的最大食物链) 我们称之为 类食物链
既然 食物链中的生物 可以看成 节点,那么 最佳生产者 的入度一定为 , 而 最佳消费者 的出度也为
思路引导
想要找到一条 最大食物链 ,那么这条路径的 起点 入度要为0,终点 出度要为0。 故:
既要记录入度,还要记录出度!
现在的问题转换成了,如何找到图中所有 左端点入度为0 且 右端点出度为0 的路径的数量
正解
我们拿起笔,在草稿纸上画一个图进行推算。接下来将使用 样例 进行举例。
(将 最佳生产者 涂上 蓝色,最佳消费者 涂上 红色)
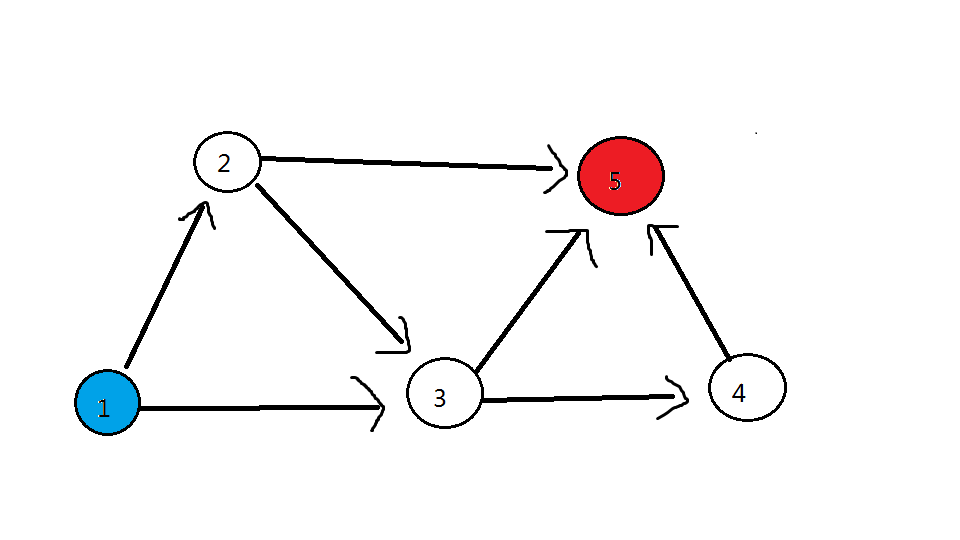
发现: 答案为 到所有 红色点 的路径条数的 总和
(这里的 路径条数总和 不是 连向它有几条边 ,而是以它结束的 最大食物链 数量的总和)
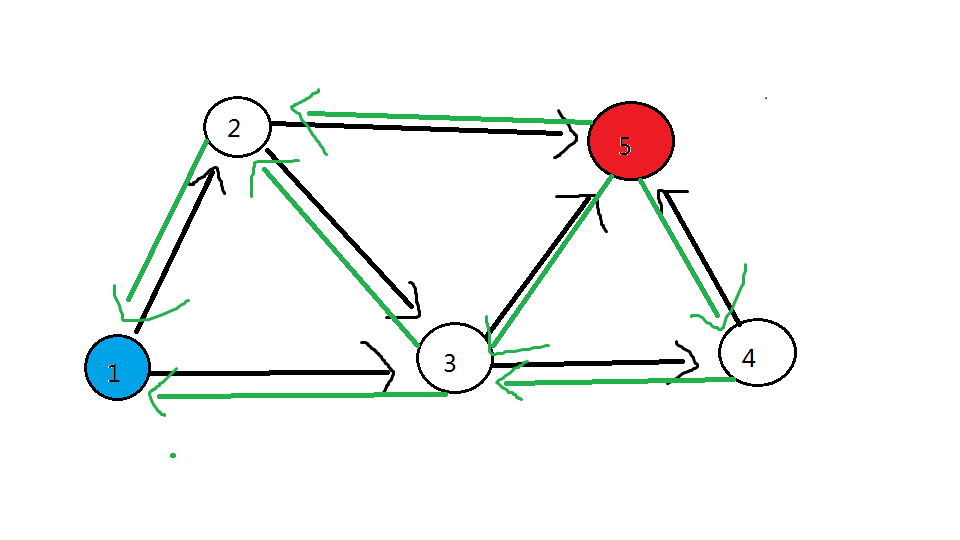
对于上图, 号点的对应路径数量 取决于:以 到 号点的三个点( 号、 号、 号) 结尾的 类食物链 条数的总和。
而 以 号、 号、 号 结尾的 类食物链 取决于:以 可以到达 号、号、号点 的点 结尾的 类食物链 条数的总和。
以此类推,显然对于 以 任一点 结尾的 类食物链 的数量,都取决于 蓝色点
各点数量对应关系在下图用绿色边标注
重点:
使用拓扑排序,由题意得知 排序第一轮被删掉的点 一定是 蓝色点(最佳生产者),而令 蓝色点 的答案为 。
当第一轮删点时,将蓝色点可以到的点 的答案 都加上 蓝色点的 答案(即加 )。
即:拓扑排序 需要删除的点的答案 都累加到 它可以到达的点 上面去
这样我们就将边的累加 转换到了 点之间的累加。
最后累加所有 红色点(最佳消费者) 的答案,输出即可。
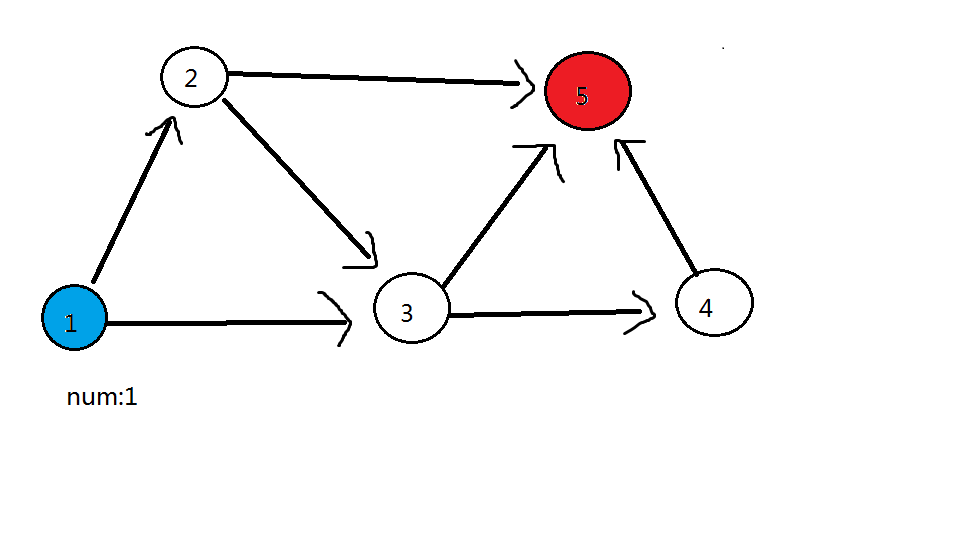
以第 $i$ 号点结束的 类食物链 数量 = 以 可到达 $i$ 号点 的点 结尾的 类食物链 数量的和以下是模拟操作过程:
加载时间较慢,请稍等第一轮:删除 号蓝色点, 号蓝色点可以到的点( 号点、 号点)都加
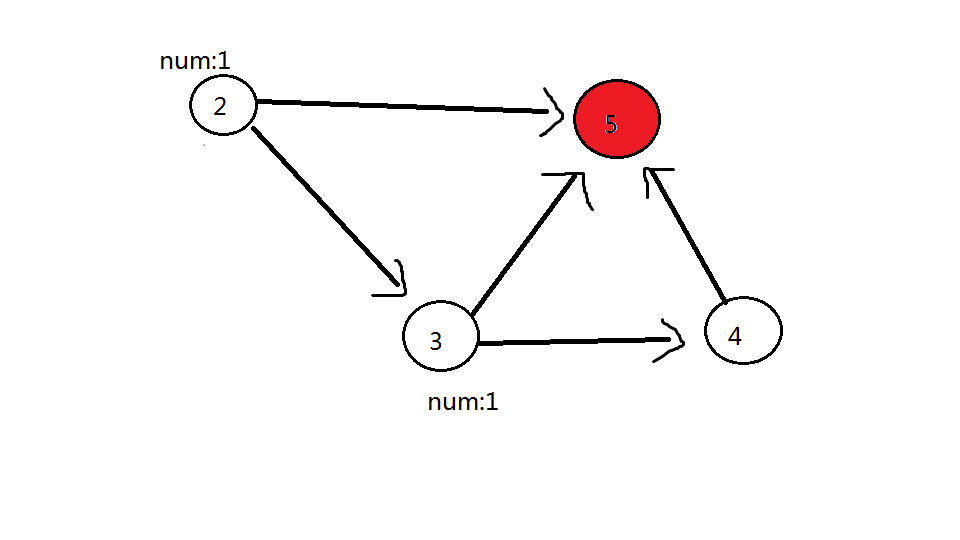
第二轮:删除 号点, 号点可以到的点( 号点、 号红色点)都加 。此时 号点答案为 , 号点答案为
第三轮:删除 号点, 号点可以到的点( 号点、 号红色点)都加 。此时 号点答案为 , 号点答案为
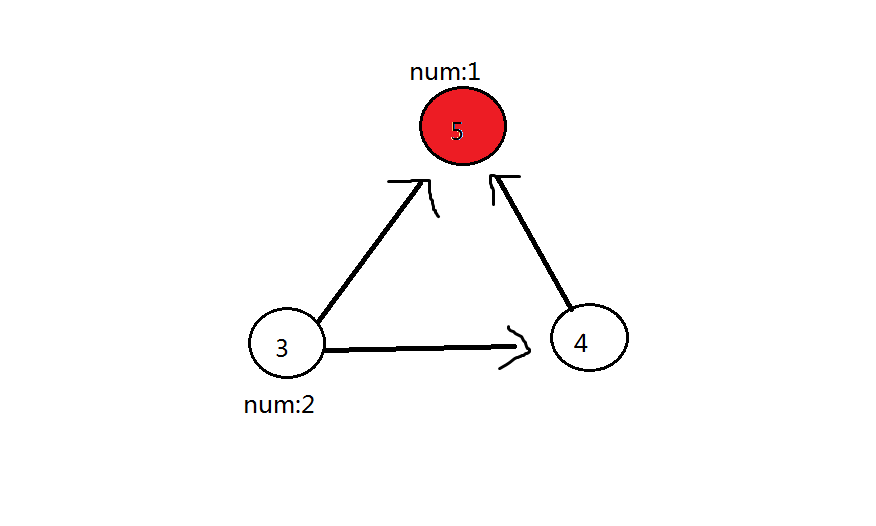
第四轮:最后删除 号点, 号点可以到的点( 号红色点)加 ,此时 号点答案为
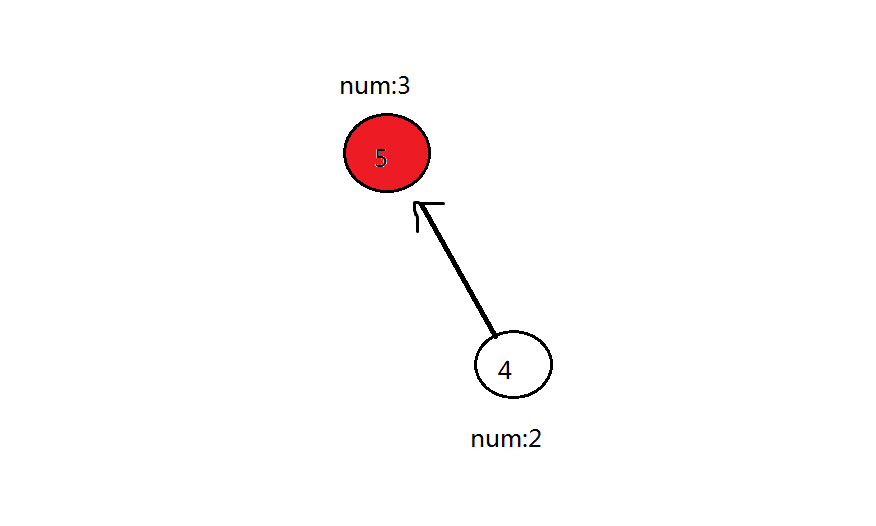
可见全图只有 号一个红色点,那么答案就是 号点的答案———— 了
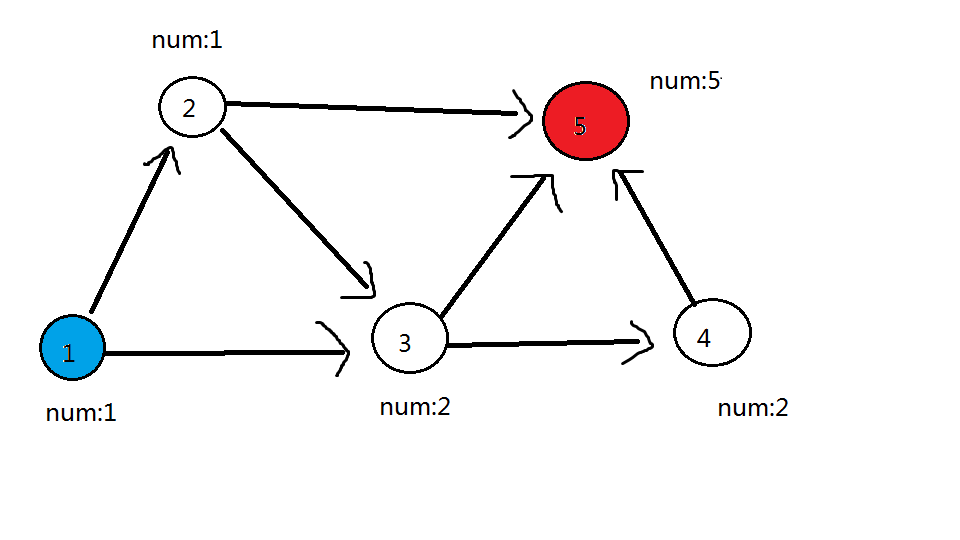
那么代码实现就很简单了!
上代码:
#include<bits/stdc++.h> #include<cctype> #pragma GCC optimize(2) #define ll long long #define rg register #define New int //上面这些花里胡哨的东西请忽略 using namespace std; inline New read()//快速读入 { New X = 0,w = 0; char ch = 0; while(!isdigit(ch)) { w |= ch == '-'; ch=getchar(); } while(isdigit(ch)) { X = (X << 3) + (X << 1) + (ch ^ 48); ch = getchar(); } return w ? -X : X; } char F[200] ; inline void write(New x) //快速输出 { if(x == 0) { putchar('0'); return; } New tmp = x > 0 ? x : -x; int cnt = 0; if(x < 0) putchar( '-' ); while(tmp > 0) { F[cnt++] = tmp % 10 + '0'; tmp /= 10; } while(cnt > 0) putchar(F[--cnt]) ; } const int N = 5e3 + 2; //定义常量大小 const int mod = 80112002; //定义最终答案mod的值 int n, m; //n个点 m条边 int in[N], out[N]; //每个点的入度和出度 vector<int>nei[N]; //存图,即每个点相邻的点 queue<int>q; //拓扑排序模板所需队列 int ans; //答案 int num[N]; //记录到这个点的类食物连的数量,可参考图 signed main() { n = read(), m = read(); for(rg int i = 1; i <= m; ++i) { //输入边 int x = read(), y = read(); ++in[y], ++out[x]; //右节点入度+1,左节点出度+1 nei[x].push_back(y); //建立一条单向边 } for(rg int i = 1; i <= n; ++i) //初次寻找入度为0的点(最佳生产者) if(!in[i]) { //是最佳生产者 num[i] = 1; //初始化 q.push(i); //压入队列 } while(!q.empty()) { //只要还可以继续Topo排序 int tot = q.front();//取出队首 q.pop();//弹出 int len = nei[tot].size(); for(rg int i = 0;i < len; ++i) { //枚举这个点相邻的所有点 int next = nei[tot][i]; //取出目前枚举到的点 --in[next];//将这个点的入度-1(因为目前要删除第tot个点) num[next] = (num[next] + num[tot]) % mod;//更新到下一个点的路径数量 if(in[next] == 0)q.push(nei[tot][i]);//如果这个点的入度为0了,那么压入队列 } } for(rg int i = 1; i <= n; ++i) //寻找出度为0的点(最佳消费者) if(!out[i]) //符合要求 ans = (ans + num[i]) % mod;//累加答案 write(ans);//输出 return 0;//end }这道题主要磨炼思维。
- 1
信息
- ID
- 2938
- 时间
- 1000ms
- 内存
- 125MiB
- 难度
- 3
- 标签
- 递交数
- 0
- 已通过
- 0
- 上传者
