自动搬运

查看原文

来自洛谷，原作者为

	crazydave **

搬运于2025-08-24 21:51:51，当前版本为作者最后更新于2018-02-07 19:58:36，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

#思路# 老师上课讲的例题，方法真的很神奇。

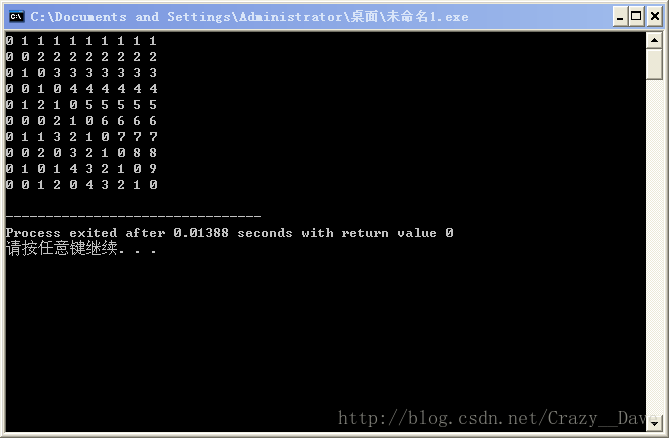
观察样例，如果没有发现什么的话，就模拟打出一张表好了：(横坐标为x, 纵坐标为y)

显然每一横行加起来就是答案，神奇的是在于纵行！（不要问我怎么发现的）。

每一纵行的意义即是，对于一个固定的i, x递增时的$x ~mod ~ i$。可以发现它是以i个为循环的数列。

处理上面一个数列复杂度较高，但是我们可以这样处理：发现对于一个固定的i, x递增时的 x-（x mod i），它便是每i项增加i的一个数列。于是我们可以每i个数打一个标记，标记意为增加i。

然后我们可以发现，f(x)可以从f(x-1)推到，便是f(x-1)+n-1-标记。（类似于前缀和+差分维护吧） #代码#

#include <iostream>
#include <algorithm>
#include <cstdio>
using namespace std;
long long n,j,temp,ans,tag[MAXN]; //tag数组即为标记

int main(){
  scanf("%lld",&n);
  for(int i=2; i<=n; i++)
	  for(int j=i; j<=n; j+=i)
		  tag[j]+=i;  //处理tag数组,每i位加i
  for(int i=1; i<=n; i++)
  {
      ans+=n-tag[i]-1;
	  printf("%lld ",ans); //递推得出答案
  }
  return 0;
}