自动搬运

查看原文

来自洛谷，原作者为

	BearBrine 这个家伙很懒，只留下了这句话

搬运于2025-08-24 21:50:28，当前版本为作者最后更新于2020-12-26 00:52:39，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

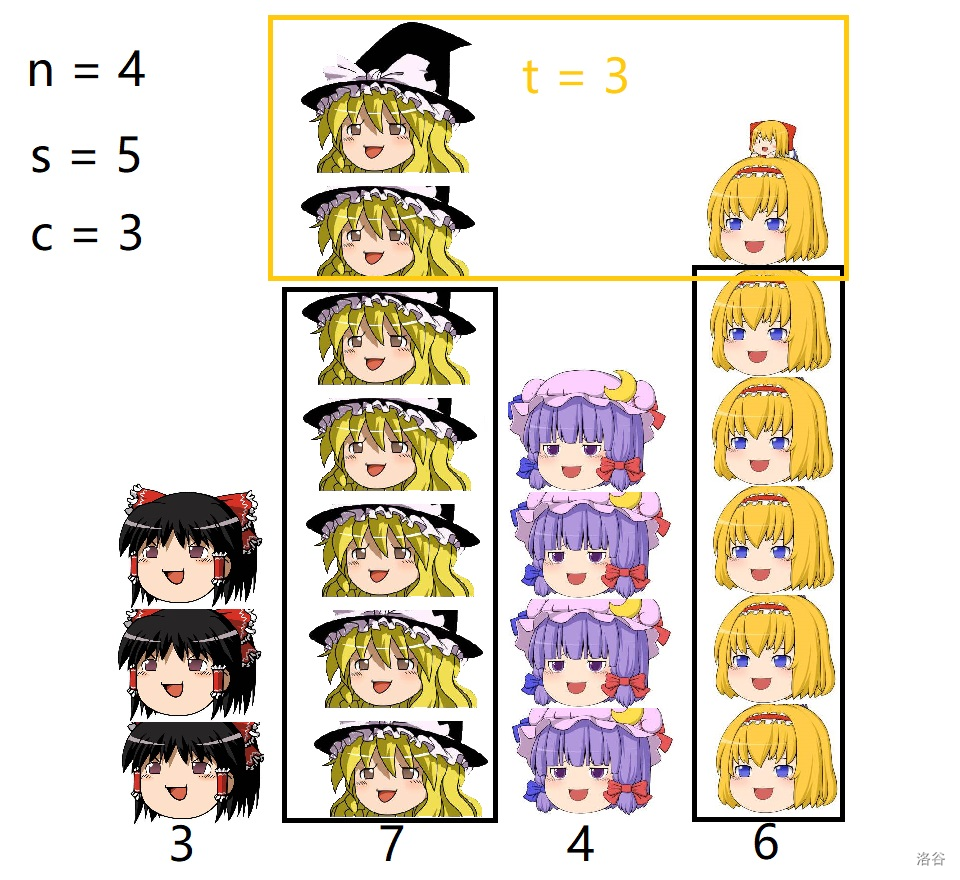
来一发比较好理解的题解。首先把题目想象成叠馒头，有 $n$ 种不同的馒头，

那么询问就变成了每次从不同的 $c$ 种馒头里各取一个，问能否取 $s$ 次。

由于每种馒头最多取 $s$ 个，于是考虑把多于 $s$ 的馒头削成 $s$ 个。

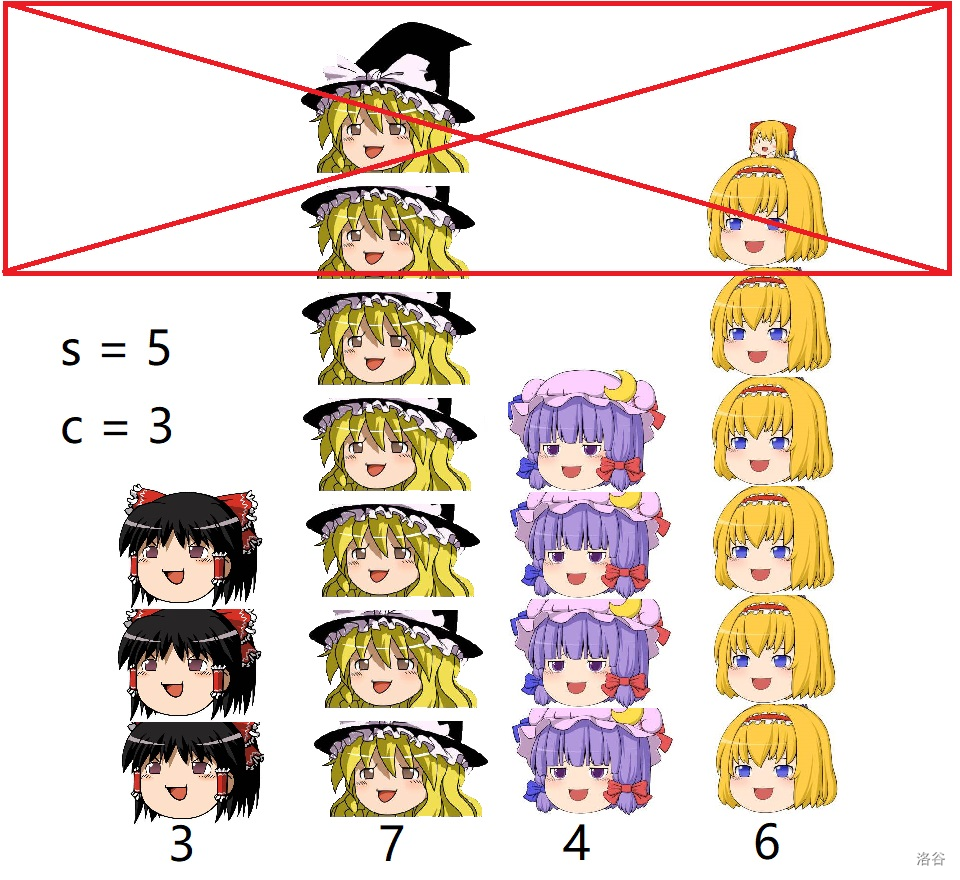
于是我们尝试把剩下的馒头构造成高为 $s$ 的 $c$ 叠馒头，然后从上往下一层一层拿就好了。

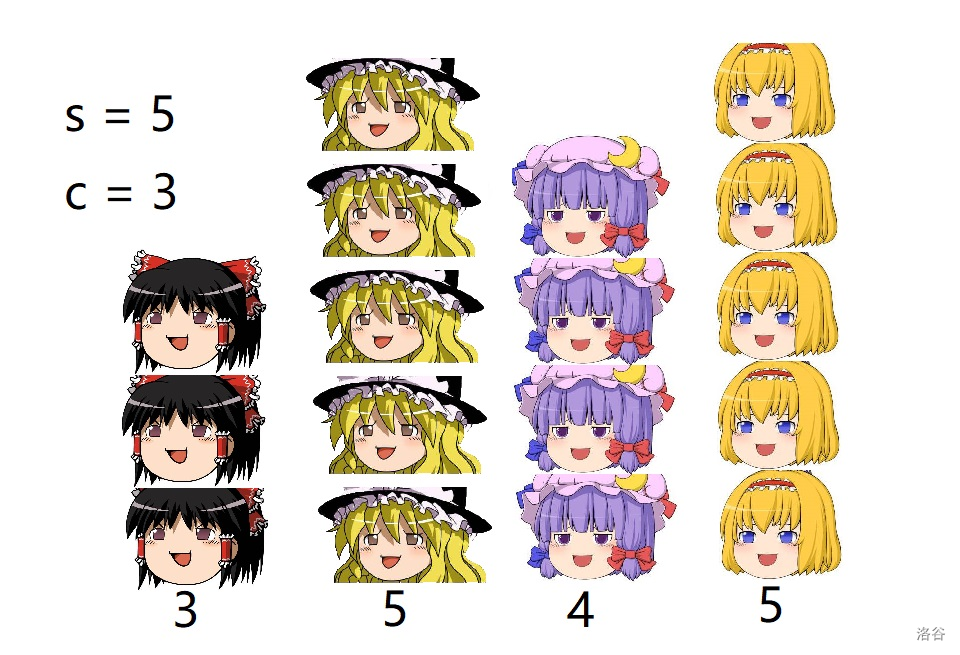
但是题目要求每次拿的馒头不能出现同种的，也就是每层不能有同种的馒头，所以上面这种叠法其实是不可行的。

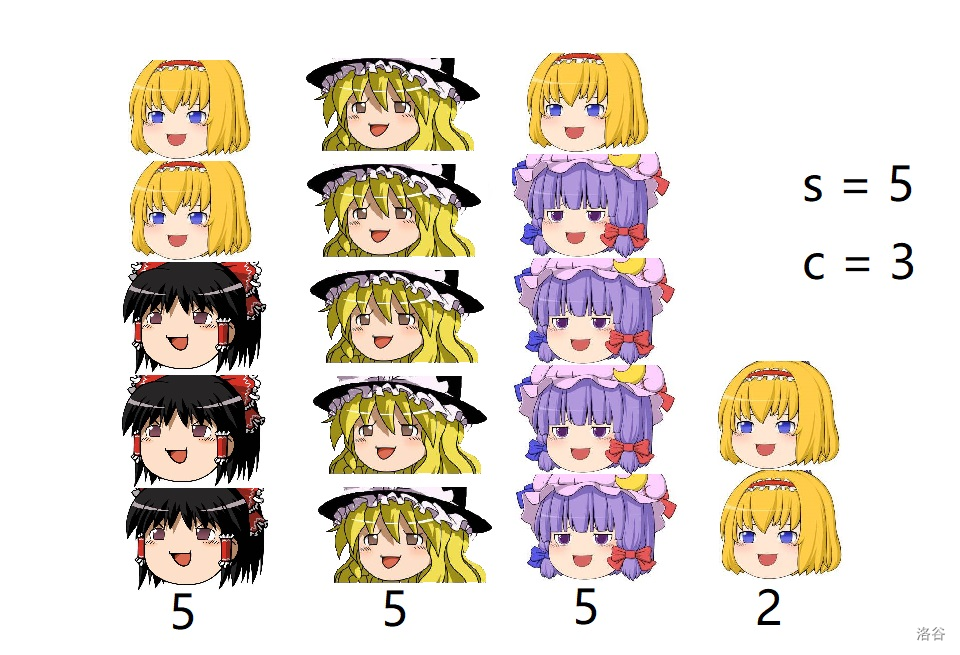
注意到每种馒头最多有 $s$ 个，于是我们把每一叠的馒头叠到它左边那叠上面，剩下的再自成一叠。

于是这样每层馒头都不会出现同种的，并且每个馒头都能被利用上。

那么只要馒头的数量够 $c \times s$ 就一定能构造出 $c$ 叠高为 $s$ 的每层各不同的馒头。

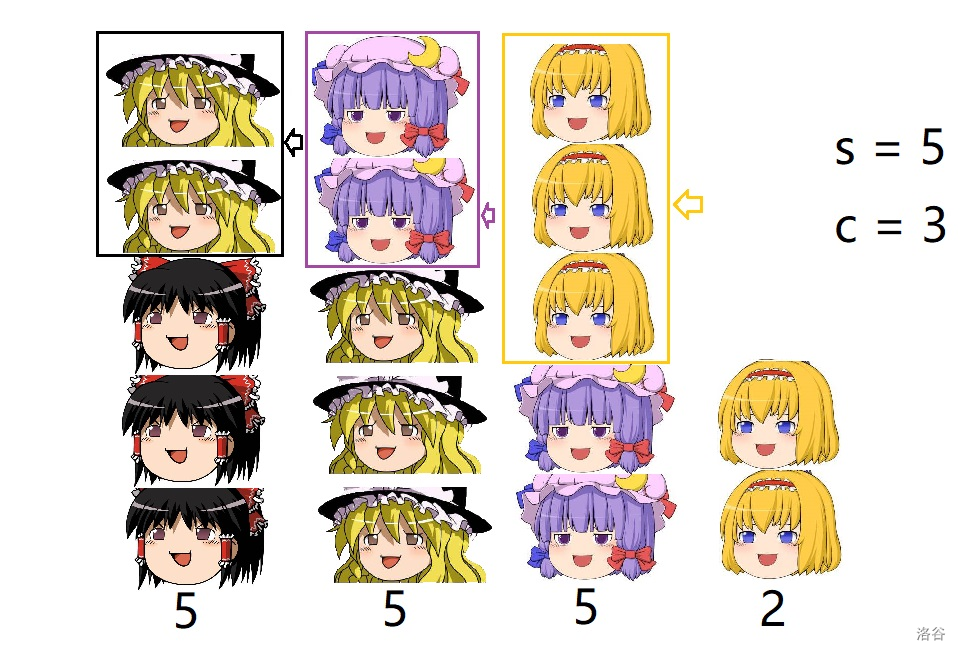
于是问题变成削掉比 $s$ 高的部分的馒头后，剩下的够不够 $c \times s$ 个。

那么怎么求高出来的那部分馒头的数量？

很显然就是每个有高出来的馒头去掉它下面的 $s$ 个馒头，剩下的馒头数的和。

所以只要知道大于 $s$ 的馒头的种类数与数量和就行了。

当然你也可以反过来求小于等于 $s$ 的馒头数和种类数。

显然在线平衡树，或者离线树状数组就解决了。

话说这题平衡树（目前最快）好像跑的比树状数组还快QAQ （可能我树状数组写丑了）

树状数组：

#include <cstdio>
#include <algorithm>
#define LL long long

char ch, sig;
template <typename _tp>
inline void rd(_tp &num)
{
    num = 0, sig = 1, ch = getchar();
    while(ch < '0' || ch > '9') {
        if(ch == '-') sig = -1;
        ch = getchar();
    }
    do{
        num = num * 10 + ch - '0';
        ch = getchar();
    }while(ch >= '0' && ch <= '9');
    num *= sig;
}

// -------------------- 上板子下正片 -------------------- //

#define MAXN 1000005

int n, m;
LL tr1[MAXN], tr2[MAXN]; //tr1是数量和，tr2是种类数
#define lowbit(x) ((~(x) + 1) & x)
inline void tradd(LL *tr, int p, int num){
    while(p <= m + 1) tr[p] += num, p += lowbit(p);
}
inline LL trqry(LL *tr, int p){
    LL sum = 0;
    while(p) sum += tr[p], p ^= lowbit(p);
    return sum;
}
char op[MAXN];
int t1[MAXN], t2[MAXN], ts[MAXN];
int bsearch(int num){ //离散化查询
    int l = 1, r = m + 1, mid;
    while(l < r){
        mid = (l + r) >> 1;
        if(ts[mid] < num) l = mid + 1;
        else if(ts[mid] > num) r = mid - 1;
        else return mid;
    }
    return l;
}
int arr[MAXN];

int main()
{
    rd(n), rd(m);
    for(int i = 1; i <= m; ++i) {
        do ch = getchar(); while(ch != 'U' && ch != 'Z');
        op[i] = ch; rd(t1[i]), rd(t2[i]); ts[i] = t2[i];
    }
    ts[m + 1] = 0;
    std::sort(ts + 1, ts + m + 2); //离散化
    for(int i = 1; i <= m + 1; ++i) arr[i] = 1;
    int tbs = bsearch(0); LL tmp;
    tradd(tr2, tbs, n);
    tradd(tr2, tbs + 1, -n);
    for(int i = 1; i <= m; ++i)
    if(op[i] == 'U') {
        tbs = bsearch(t2[i]);
        tradd(tr1, arr[t1[i]], -ts[arr[t1[i]]]);
        tradd(tr1, tbs, ts[tbs]);
        tradd(tr2, arr[t1[i]] + 1, 1);
        tradd(tr2, tbs + 1, -1);
        arr[t1[i]] = tbs;
    } else {
        tbs = bsearch(t2[i]);
        tmp = (t1[i] - trqry(tr2, tbs)) * t2[i];
        printf("%s\n", trqry(tr1, tbs - 1) >= tmp ? "TAK" : "NIE");
    }

    return 0;
}

平衡树：

#include <cstdio>
#include <cctype>
#include <algorithm>
#define uint unsigned int
#define uLL unsigned long long

#define mmin(A, B) (((A) < (B)) ? (A) : (B))
#define mmax(A, B) (((A) > (B)) ? (A) : (B))

struct quickio 
{
    char ch, sig;
    
    template <typename _tp>
    inline quickio& operator >> (_tp &num) {
        num = 0, sig = 1, ch = getchar();
        while(ch < '0' || ch > '9') {
            if(ch == '-') sig = -1;
            ch = getchar();
        }
        do {
            num = num * 10 + ch - '0';
            ch = getchar();
        } while(ch >= '0' && ch <= '9');
        num *= sig;
        return *this;
    }
    inline quickio& operator >> (char &tc) {
        do tc = getchar(); while(isspace(tc));
        return *this;
    }

    inline quickio& operator << (char *ts) {
        while(*ts != '\0') putchar(*(ts++));
        return *this;
    }
} qio;

// -------------------- 上板子下正片 -------------------- //

#define MAXN 1000005

uint n, m;

inline void Change();
inline void Query();

int main()
{
    qio >> n >> m;
    char tc;
    while(m--) {
        qio >> tc;
        switch (tc)
        {
        case 'U': Change(); break;
        case 'Z': Query(); break;
        
        default:
            break;
        }
    }

    return 0;
}

uint ar[MAXN], acnt = 0;
//写的AVL树
struct node { 
    uint ln, rn;
    uint siz, cnt, h;
    uint val;
    uLL sum;
} bst[MAXN]; 
uint bcnt = 0, rt = 0;
//左儿子右也是儿子
#define ls(A) (bst[A].ln)
#define rs(A) (bst[A].rn)

inline uint newnode() {
    ++bcnt;
    ls(bcnt) = rs(bcnt) = 0;
    bst[bcnt].siz = bst[bcnt].cnt = 1;
    bst[bcnt].h = 1;
    return bcnt;
}
inline void update(uint p) { //更新节点
    bst[p].siz = bst[ls(p)].siz + bst[rs(p)].siz + bst[p].cnt;
    bst[p].h = mmax(bst[ls(p)].h, bst[rs(p)].h) + 1;
    bst[p].sum = bst[ls(p)].sum + bst[rs(p)].sum + (uLL)bst[p].val * bst[p].cnt;
}

inline void rotate(uint p, bool rr) {
    uint tp;
    if(rr) {
        tp = ls(p);
        ls(p) = ls(tp);
        ls(tp) = rs(tp);
        rs(tp) = rs(p);
        rs(p) = tp;
    } else {
        tp = rs(p);
        rs(p) = rs(tp);
        rs(tp) = ls(tp);
        ls(tp) = ls(p);
        ls(p) = tp;
    }
    std::swap(bst[p].cnt, bst[tp].cnt);
    std::swap(bst[p].val, bst[tp].val);
    update(tp), update(p);
}

inline void maintain(uint p) {
    if(bst[ls(p)].h > bst[rs(p)].h + 1) { //uint不能直接相减，惨痛的教训QwQ
        if(bst[ls(ls(p))].h < bst[rs(ls(p))].h) 
            rotate(ls(p), false);
        rotate(p, true);
    } else if(bst[rs(p)].h > bst[ls(p)].h + 1) {
        if(bst[rs(rs(p))].h < bst[ls(rs(p))].h)
            rotate(rs(p), true);
        rotate(p, false);
    } else update(p);
}
void doInsert(uint val, uint p = rt) { //插入
    uint *tp = &p;
    if(val < bst[p].val) tp = &ls(p);
    else if(bst[p].val < val) tp = &rs(p);
    if(*tp == p) ++bst[p].cnt, update(p);
    else if(!(*tp)) {
        *tp = newnode();
        bst[*tp].val = bst[*tp].sum = val;
        update(p);
    } else doInsert(val, *tp), maintain(p);
}
void doDelete(uint val, uint p = rt) { //偷懒版删除qwq
    uint *tp = &p;
    if(val < bst[p].val) tp = &ls(p);
    else if(bst[p].val < val) tp = &rs(p);
    if(*tp == p) --bst[p].cnt, update(p);
    else doDelete(val, *tp), update(p);
}
void getInfo(uint val, uint &rk, uLL &sum, uint p = rt) { //获取排名与和
    if(!p) return;
    if(val < bst[p].val) getInfo(val, rk, sum, ls(p));
    else { 
        rk += bst[p].cnt + bst[ls(p)].siz;
        sum += (uLL)bst[p].val * bst[p].cnt + bst[ls(p)].sum;
        getInfo(val, rk, sum, rs(p));
    }
}

inline void Change() {
    uint tp, tn;
    qio >> tp >> tn;
    if(ar[tp]) doDelete(ar[tp]), --acnt;
    ar[tp] = tn;
    if(tn) {
        if(!rt) {
            rt = newnode();
            bst[rt].val = bst[rt].sum = tn;
        } else doInsert(tn);
        ++acnt;
    }
}
inline void Query() {
    uint tc, ts;
    qio >> tc >> ts;
    uint tnum = 0; uLL tsum = 0;
    getInfo(ts, tnum, tsum);
    if(tsum + (uLL)(acnt - tnum) * ts >= (uLL)tc * ts)
        qio << "TAK\n";
    else qio << "NIE\n";
}