自动搬运

查看原文

来自洛谷，原作者为

	_zhangcx 支持互关 || Bocchi the Rock 第二季快来啊

搬运于2025-08-24 21:49:26，当前版本为作者最后更新于2025-08-19 08:34:24，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

---

这道题咋没有题解，调了我好久

题意：二维平面上有 $z$ 个点，给定 $p$ 个询问，每次两个点 $P1$、$P2$，求距离 $P1$ 更近的点的个数、距离 $P2$ 更近的点的个数以及与 $P1$、$P2$ 距离相同的点的个数。距离为曼哈顿距离，横坐标值域为 $[1,n]$，纵坐标值域为 $[1,m]$。

首先发现只需要考虑处理距离 $P1$ 更近的点即可，因为问题的对称性。

以下记点 $A$ 的横坐标为 $X_A$，纵坐标为 $Y_A$。对于 $z$ 个点中的任意一个点 $A$，我们列出关系式：$|X_A - X_{P1}| + |Y_A - Y_{P1}| < |X_A - X_{P2}| + |Y_A - Y_{P2}|$。

根据初中数学知识，$X_A$、$Y_A$ 都有 3 种情况，一共 9 种情况，我们把它们在图像中表示出来。假设给定的 $X_{P1} \le X_{P2}$，$Y_{P1} \le Y_{P2}$。

rt，显然区域 2、4、6、8，区域 1、9，区域 3、7，区域 5 为四种不同情况，以下进行分讨：

记 $a = X_{P2} - X_{P1}$，$b = Y_{P2} - Y_{P1}$

1. 区域 2、4、6、8

以区域 8 为例，$\operatorname{dist}(P1,A) = \Delta y + (a - \Delta x) + b$，$\operatorname{dist}(P2,A) = \Delta x + \Delta y$。

要保证 $\operatorname{dist}(P1,A) < \operatorname{dist}(P2,A)$，即要保证 $\Delta y + (a - \Delta x) + b < \Delta x + \Delta y$，即 $\Delta x > \frac{a + b}{2}$，带入 $\Delta x = X_{P2} - X_A$ 得 $X_A < X_{P2} - \frac{a + b}{2}$。

因而该区域满足条件的点 $A$ 需满足 $X_A \in [X_{P1},X_{P2}] \cap [0,X_{P2} - \frac{a + b}{2})$，$Y_A \in (Y_{P2}, m]$。

2. 区域 1、9

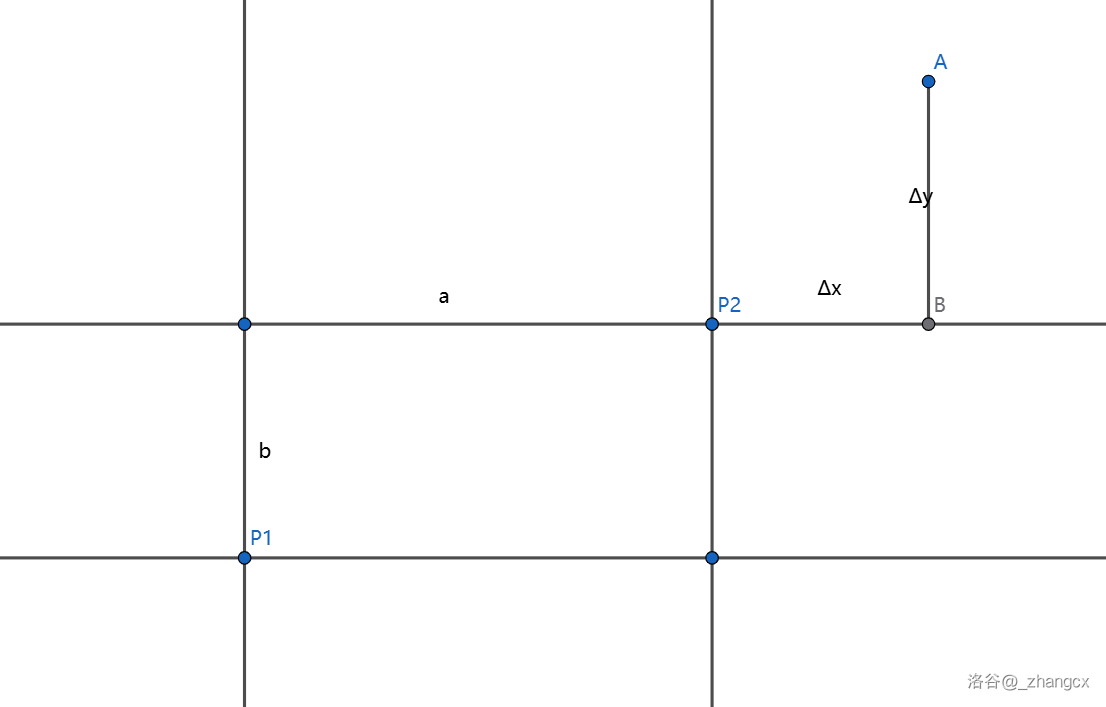
以区域 9 为例，显然 $\operatorname{dist}(P1,A) > \operatorname{dist}(P2,A)$。（当然 P1 = P2 的情况需要特判）

因此该区域所有点均不满足。

3. 区域 3、7

以区域 7 为例，$\operatorname{dist}(P1,A) = \Delta x + \Delta y + b$，$\operatorname{dist}(P2,A) = \Delta x + \Delta y + a$。

可以发现当 $b < a$ 时 $\operatorname{dist}(P1,A) < \operatorname{dist}(P2,A)$。

所以当 $b < a$ 时该区域所有点均满足。

4. 区域 5

区域 5 中，$\operatorname{dist}(P1,A) = (a - \Delta x) + (b - \Delta y)$，$\operatorname{dist}(P2,A) = \Delta x + \Delta y$。

要保证 $\operatorname{dist}(P1,A) < \operatorname{dist}(P2,A)$，即要保证 $(a - \Delta x) + (b - \Delta y) < \Delta x + \Delta y$，即 $\Delta x + \Delta y > \frac{a + b}{2}$，带入 $\Delta y = Y_{P2} - Y_A$、$\Delta x = X_{P2} - X_A$ 得 $X_A + Y_A < X_{P2} + Y_{P2} - \frac{a + b}{2}$。

因而该区域满足条件的点 $A$ 需满足 $X_A \in [X_{P1},X_{P2}]$，$Y_A \in [Y_{P1}, Y_{P2}]$，$X_A + Y_A \in [0, X_{P2} + Y_{P2} - \frac{a + b}{2})$。

到这儿分类讨论结束。

如果 $P1$、$P2$ 不是偏序关系怎么办？一开始我想的是再分讨一次，但是太麻烦，我们可以考虑将整个平面反转。具体的，我们考虑翻转 $(1,1)(n,m)$ 这个矩形，若是左右翻转则所有横坐标 $X$ 变为 $n + 1 - X$，若是上下翻转则所有纵坐标 $Y$ 变为 $m + 1 - Y$。

现在尝试维护答案。我们发现前三类只与 $X_A$，$Y_A$ 有关，且均为一段区间，考虑二维偏序，扫描线 + 树状数组即可。

第 4 类（即区域 5）另外有个 $X_A + Y_A$ 的限制，是三维偏序。第一次打的时候用了二维线段树，空间爆炸喜提暴力分，于是专门新学了 KD-Tree 来用。

不幸的是，KD-Tree 常数过大，加上代码自带大常数，无法 AC。

尝试优化。我们在统计答案的时候换一个思路：统计 $\operatorname{dist}(P1,A)<\operatorname{dist}(P2,A)$、与 $\operatorname{dist}(P1,A)\le\operatorname{dist}(P2,A)$ 的点的数量 $a1$、$a2$。后者只是在原先的推导上，将小于改为小于等于。那么其实它们有很多询问是重叠的，甚至是相同的，可以在相同的时候一块维护。

注意三个答案要变为 $a1$，$z - a2$，$a2 - a1$。

另外，KD-Tree 的询问速度较慢，可以把询问排一下序，相邻相同的询问使用同一个答案。

最后再加上一些各类广为人知的卡常技巧就可以 AC 啦。

Code