自动搬运

查看原文

来自洛谷，原作者为

	poorpool **

搬运于2025-08-24 21:46:45，当前版本为作者最后更新于2018-01-19 11:41:00，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

前置技能：poj3041

如果是二维平面有一些方块，这些方块被染了黑色，你每次可以选择 $(x,y)$ 的区域染成白色，代价是 $\min(x,y)$，问你付出的最小代价

显然我们不会这么染

因为这样我们的代价是 $\min(x,y)$，为了研究的方便我们假设 $x$ 比 $y$ 小，那我们就相当于染 $x$ 次 $1 \times y$ 的区域，因此一次染一片总是不如一次染一条的。下面这么染就很好

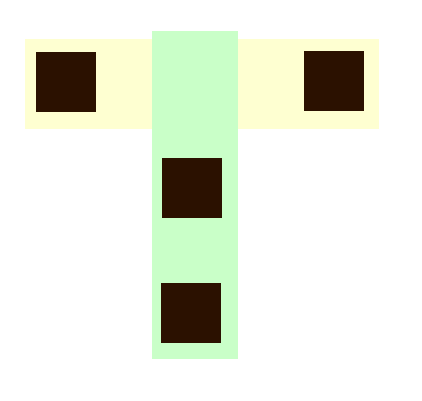
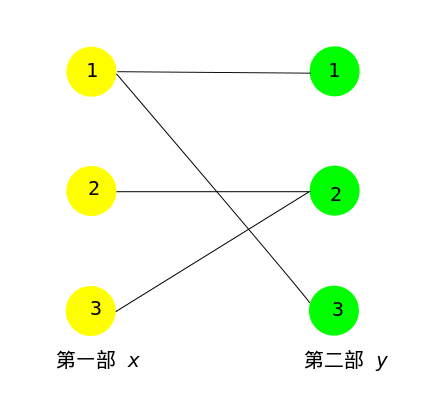
所以我们建立二分图，对于每个黑色块 $(x,y)$，我们将其处于第一部的 $x$ 与处于第二部的 $y$ 连接，求一个最小点覆盖。二分图中最小点覆盖=最大匹配，就得到了答案。

回到本题，题目中扩展到了三维空间，我们也有类似的想法。然而我们并不会三分图匹配这种东西……

观察到 $abc \leq 5000$，反证法可以轻易地证出 $a,b,c$ 中有一个 $\leq \sqrt[3]{5000} \approx 17.1$，为了研究方便我们钦定是 $a \leq \sqrt[3]{5000}$，这样就暴力枚举 $1\ldots a$ 中的某一层是直接削掉还是一会儿再处理（只有这两种情况，别的都不好，想一想为什么）。

对于没有被直接削掉的层，我们把它们剥离出来，然后拍扁成二维平面上的问题求解。

代码。跑得不是很快，借鉴了一下网上的代码

#include <iostream>
#include <cstring>
#include <cstdio>
using namespace std;
int T, hea[5005], cnt, a, b, c, minn, sx[4][5005], uu, ans, lnk[5005], qaq;
bool isn[5005], qwq[25], vis[5005];
struct Edge{
    int too, nxt;
}edge[5005];
void add_edge(int fro, int too){
    edge[++cnt].nxt = hea[fro];
    edge[cnt].too = too;
    hea[fro] = cnt;
}
bool dfs(int x){
    for(int i=hea[x]; i; i=edge[i].nxt){
        int t=edge[i].too;
        if(!vis[t]){
            vis[t] = true;
            if(!lnk[t] || dfs(lnk[t])){
                lnk[t] = x;
                return true;
            }
        }
    }
    return false;
}
void work(int x){
    for(int i=1; i<=b; i++)    hea[i] = 0;
    cnt = 0;
    for(int i=1; i<=c; i++)    lnk[i] = 0;
    int tmp=0;
    for(int i=0; i<a; i++){
        if(x&(1<<i))    qwq[i+1] = false, tmp++;
        else    qwq[i+1] = true;
    }
    for(int i=1; i<=qaq; i++)
        if(qwq[sx[1][i]])
            add_edge(sx[2][i], sx[3][i]);
    for(int i=1; i<=b; i++){
        for(int j=1; j<=c; j++)    vis[j] = false;
        if(dfs(i))    tmp++;
    }
    ans = min(tmp, ans);
}
int main(){
    cin>>T;
    while(T--){
        qaq = 0;
        ans = 0x3f3f3f3f;
        scanf("%d %d %d", &a, &b, &c);
        minn = min(a, min(b, c));
        for(int i=1; i<=a; i++)
            for(int j=1; j<=b; j++)
                for(int k=1; k<=c; k++){
                    scanf("%d", &uu);
                    if(!uu)    continue;
                    sx[1][++qaq] = i;
                    sx[2][qaq] = j;
                    sx[3][qaq] = k;
                }
        if(minn==b)    swap(a, b), swap(sx[1], sx[2]);
        else if(minn==c)    swap(a, c), swap(sx[1], sx[3]);
        for(int i=0; i<(1<<a); i++)
            work(i);
        printf("%d\n", ans);
    }
    return 0;
}