自动搬运

查看原文

来自洛谷，原作者为

	Froranzen 你没有那个实力，不要再欺骗自己了

搬运于2025-08-24 21:40:40，当前版本为作者最后更新于2020-12-20 00:54:17，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

---

题目传送门

---

1.第一种 $O(n^3)$ 做法

本人第一个想到的做法就是用二维前缀和来暴力查找最大子矩阵。

具体来讲，就是用一个三维的 bool 数组 $vis_{i,j,k}$，表示在第 $i$ 行的第 $j \sim k$ 个数间是否有 $0$。然后在查找最大子矩阵时，在上下两边之间跑一遍循环来检查有无 $0$。

---

二维前缀和

1. 首先，设 $sum_{i,j}$，代表从 $(1,1)$ 为左上角 到 $(i, j)$ 为右下角的矩形区域的加权和。

令 $(i, j)$ 表示位置为从左往右数第 $i$ 列，从上往下数第 $j$ 行的格子。

---

---

2. 根据上图，我们可以得出这样的公式：

$$sum_{i,j} = sum_{i-1,j} + sum_{i,j-1} - sum_{i-1,j-1} + val_{i,j} $$

因为左下角为 $(i - 1, j - 1)$ 的矩形，在 $(i, j - 1)$ 矩形中加了一次，在 $(i - 1, j)$ 矩形中又加了一次，所以要减去矩形 $(i - 1, j - 1)$ 。

---

---

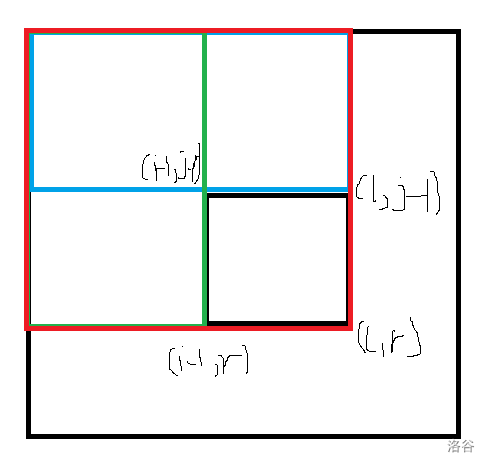
3. 如上图，我们根据 $sum$ 数组的值，可以较为容易地推出下面公式，即点 $(i,j)$ 为左上角，点 $(l,r)$ 为右下角的矩阵中值的和为：

$$sum_{l, r} - sum_{i-1,r} - sum_{l,j-1} + sum_{i-1,j-1} $$

理解了二维前缀和，这道题就没什么难度了。

---

代码

---

#include <cstdio>
#include <cstring>
using namespace std;

int _map[333][333];
int qwq[333][333]; 	//二维前缀和，维护数值
bool wqw[333][333][333];  //维护有无0
int n, m;
int ans;

inline int min (int a, int b) {
	return a < b ?a :b;
}

inline int max (int a, int b) {
	return a >b ?a :b;
}

int main () {
	scanf ("%d %d", &n, &m);
	for (int i(1); i <= n; ++i)
		for (int j(1); j <= m; ++j)
			scanf ("%d", &_map[i][j]);
	for (int i(1); i <= n; ++i) {
		for (int j(1); j <= m; ++j) {
			qwq[i][j] = qwq[i][j - 1] + qwq[i - 1][j] - qwq[i - 1][j - 1] + _map[i][j];  //二维前缀和
		}
	}
	for (int i(1); i <= n; ++i) {  
		for (int l(1); l <= m; ++l) {  //枚举一个点
			int len = m - l;  //求出剩余长度
            bool flag = false;  //标记
			for (int s(0); s <= len; ++s) {  //循环一遍长度
                if (flag == true) wqw[i][l][l+s] = 1;  //如果之前已经有过'0'，直接记录为有'0'
				if (!_map[i][l + s]) {  //如果当前点是'0'
					wqw[i][l][l + s] = 1;
                    flag = true;
				}
			}
		}
	}
	for (int i(1); i <= n; ++i) {
		for (int j(1); j <= m; ++j) {  //枚举一个点
			int tmp = m - j;  //求出剩余长度
			bool flag = false;  //标记
			int orz;  //标记
			for (int len(0); len <= tmp; ++len) {  //枚举长度
				for (int k(i); k <= n; ++k) {  //枚举另一个点，因为是一个矩形，所以我们只枚举行数，相应的顶点都是和上面两层枚举的顶点平行
                    if (flag && k == orz) break;  //剪枝，因为len是正序枚举，所以之前有'0'，现在到了当时的行数，一定还会有'0'
					if (wqw[k][j][j +len]) {  //有0
						flag = true;
						orz = k;  //标记
						break;
					}
					ans = max (ans, qwq[k][j +len] - qwq[i - 1][j +len] - qwq[k][j -1] + qwq[i - 1][j - 1]);  //二维前缀和公式
				}
			}
		}
	}
	printf ("%d", ans);
	return 0;
}

---

upd: 2022.10.17

这样一个暴力题解成了点赞数最多的，感觉有点误导别人了，所以本人在这里补充一下别的做法。

2.另外一种 $O(n^3)$ 做法

首先做一步转化：我们直接将 $0$ 位置的权值赋成负无穷，所以不合法的矩形的权值都变成负无穷了，然后求出新矩形的最大子矩形就是答案。

设 $w(l,r,i,j)$ 表示 $(l,r)$ 为左上端点，$(i,j)$ 为右下端点的矩形权值。

暴力 $O(n^2)$ 枚举上下边界 $l, r$，再从左往右扫右边界 $i$，维护最优左边界 $j$。答案的形式一定是 $w(1,l,i,r) - w(1,l,j-1,r)$，所以维护一个 $w(1,l,i,r)$ 的最小值即可。

时间复杂度 $O(n^3)$。

---

3. $O(n^2)$ 做法

来到正题。给 $0$ 位置赋负无穷然后求最大子矩阵的话，其实有点浪费题目给的性质了，我们能选出的矩形，一定是极大的，因为权值为正，而上面的 $O(n^3)$ 做法却抛弃了这个性质。所以我们还是考虑原来的问题。

考虑最后的矩形会长成一个什么样子：扩展一格上边界一定会使得这个矩形不合法，不然我们再扩展一格上边界显然更优。设扩展一格上边界后，第 $x$ 列会变得不合法，那我们不妨去枚举这个 $x$。即对于每个点 $(i, j)$，求出同一列，之前的第一个不合法的位置 $(i, k)$，然后去扩展这个以 $(i, k+1)$ 为右上端点，$(i, j)$ 为左下端点的矩形直到不能扩展。具体求这个左右边界，可以先求出 $(i, j)$ 在当前行里，能扩展到的边界，然后和同一列上一个矩形的左右边界取交即可。

时间复杂度 $O(n^2)$。

---

感谢您的阅读 :)