自动搬运

查看原文

来自洛谷，原作者为

	IC_QQQ **

搬运于2025-08-24 21:37:49，当前版本为作者最后更新于2019-05-13 10:21:07，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

求逆序对

但这肯定不是普通的求逆序对题目：数据范围太大了，会超时。

尽管数据范围很大，但是k不大，最多只牵涉到了2k个数。

我们举个例子：

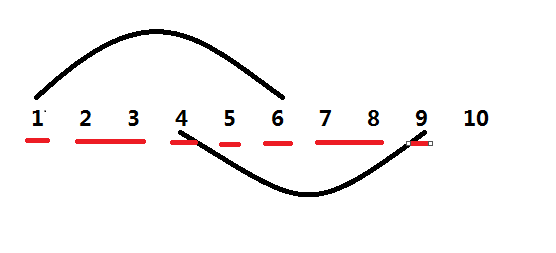
需要交换的两组数是：1—6 , 4—9。

我们可以发现，数2、3可以看做一个整体，数7、8可以看做一个整体。

也就是说，一段连续的数，我们可以把它看做一个整体，记录下它的代表元id和权值t。

什么意思呢？我们来看处理之后应该是怎样的：

（1,1) ， (2,2) ， (4,1) ， (5,1) ， (6,1) ， (7,2) ， (9,1)

我们就把所有的连续区间记做了二元组。用这个区间最小的数作代表元，权值就是区间数的个数。

然后进行交换：

（6,1），（2,2），（9,1），（5,1），（1,1），（7,2），（4,1）

剩下的就是普通的求逆序对了。

别忘了离散化。

代码：

#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int N=1e5+5;
int n,st,tot;
struct aaa{
	int x,y;
}Q[N];//记录需要交换的数
int t[2*N],id[2*N];//t:权值。id:代表元
int s[2*N],row[22*N];
ll ans,c[2*N];

int query(int val){//离散化的查询
	return lower_bound(row+1,row+1+tot,val)-row;
}

void adds(int pos,ll w){//
	for(;pos<=tot;pos+=pos&-pos) c[pos]+=w;
	return;
}

ll asks(int pos){
	ll sum=0;
	for(;pos;pos-=pos&-pos) sum+=c[pos];
	return sum;
}

int main(){
	scanf("%d",&n);
	for(int i=1;i<=n;i++){
		scanf("%d%d",&Q[i].x,&Q[i].y);
		s[i]=Q[i].x;s[i+n]=Q[i].y;
	}
	sort(s+1,s+1+2*n);
	st=unique(s+1,s+1+2*n)-(s+1);
	row[++tot]=s[1];t[tot]=1;
	for(int i=2;i<=st;i++){
		if(s[i]-s[i-1]>1){
			row[++tot]=s[i-1]+1;
			t[tot]=s[i]-s[i-1]-1;
		}
		row[++tot]=s[i];t[tot]=1;
	}
	for(int i=1;i<=tot;i++) id[i]=i;
	for(int i=1;i<=n;i++){
		int x=query(Q[i].x),y=query(Q[i].y);
		swap(t[x],t[y]);
		swap(id[x],id[y]);
	}
	for(int i=tot;i>=1;i--){
		ans+=asks(id[i]-1)*(ll)t[i];//注意，乘法 
		adds(id[i],(ll)t[i]);
	} 
	printf("%lld",ans);
	return 0;
}