自动搬运

查看原文

来自洛谷，原作者为

	BitByBit a.k.a. 海绵猴子

搬运于2025-08-24 21:37:25，当前版本为作者最后更新于2025-03-22 08:33:54，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

AC记录

题意

给你一个电路，电路中的元件有一个损坏的概率，求整个电路断路的概率。

分析

令 $P$ 为整个电路断路的概率，$P_1,P_2$ 分别为 $R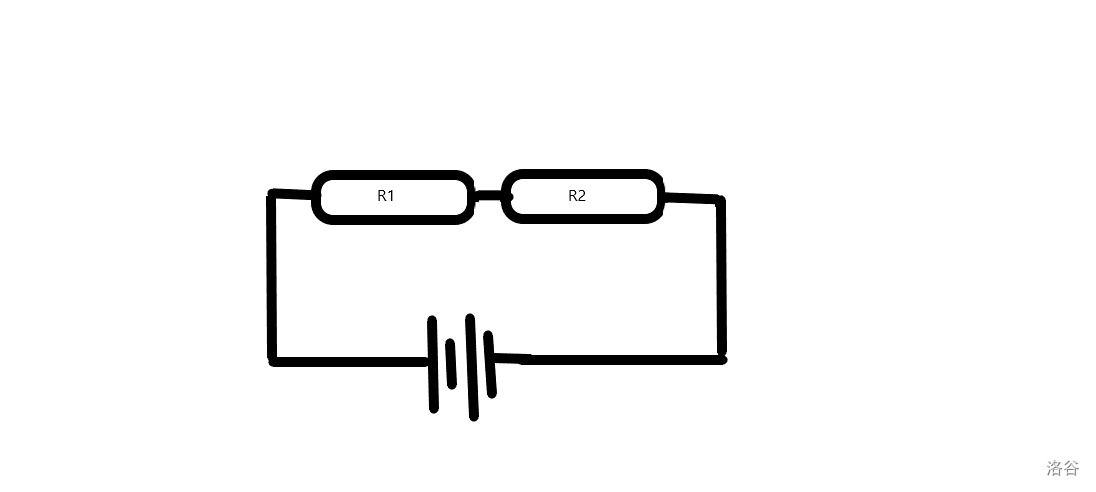_1,R_2$ 断路的概率。 如图，对于一个串联的电路，$R_1$ 和 $R_2$ 中只要有一个损坏了，整个电路就断路了。所以只有两个元件都不损坏才能使整个电路不损坏。所以根据乘法原理 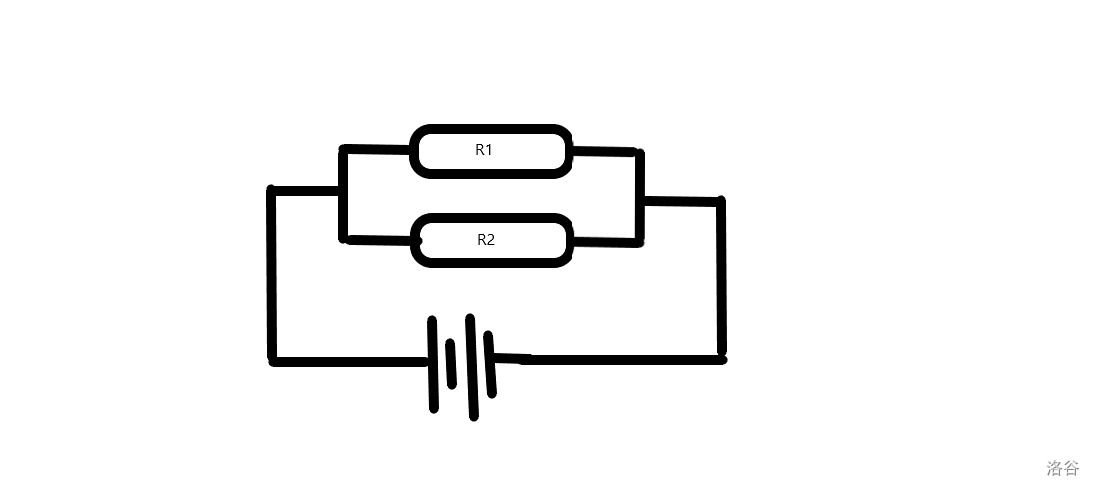$P=1-(1-P_1)\times (1-P_2)$。 同理，对于并联电路，只有两个原件断路，整个电路才断路。所以 $P=P_1 \times P_2$。

于是就把题目变成了表达式求值。

首先应匹配括号。用一个栈，每次遇到左括号就压入，遇到右括号就让栈顶括号匹配当前括号。

#define ll long long
...
stack<ll>q;
...
for(ll i=1;i<=m;i++)
    if(s[i]=='(')q.push(i);
  	else if(s[i]==')')
  	{
  		f[q.top()]=i;
  		q.pop();
  	}

然后分治处理表达式。

double dfs(ll x,ll y)//处理s[x..y]
{
	if(f[x]==y)//如果x和y匹配就把括号去掉
	{
		x++;y--;
	}
	if(x==y&&isalpha(s[x]))return a[s[x]-64];
//如果只有一个元件就返回其损坏概率
	ll k=0;
	for(ll i=x;i<=y;i++)
	{
		if(s[i]=='(')k++;
		else if(s[i]==')')k--;
		if(k==0&&s[i]==',')return 1-(1-dfs(x,i-1))*(1-dfs(i+1,y));
//找到串联的地方，分治解决两边
	}
	for(ll i=x;i<=y;i++)
	{
		if(s[i]=='(')k++;
		else if(s[i]==')')k--;
		if(k==0&&s[i]==')'&&s[i+1]=='('&&i!=y)return dfs(x+1,i-1)*dfs(i+1,y);
//找并联的地方
	}
	return 1;
}

所求就是 dfs(1,n)。

完整程序

#include<bits/stdc++.h>
#define ll long long
using namespace std;
const ll N=100010;
ll n,m;
ll f[N];
double a[N];
string s;
stack<ll>q;
double dfs(ll x,ll y)
{
	if(f[x]==y)
	{
		x++;y--;
	}
	if(x==y&&isalpha(s[x]))return a[s[x]-64];
	ll k=0;
	for(ll i=x;i<=y;i++)
	{
		if(s[i]=='(')k++;
		else if(s[i]==')')k--;
		if(k==0&&s[i]==',')return 1-(1-dfs(x,i-1))*(1-dfs(i+1,y));
	}
	for(ll i=x;i<=y;i++)
	{
		if(s[i]=='(')k++;
		else if(s[i]==')')k--;
		if(k==0&&s[i]==')'&&s[i+1]=='('&&i!=y)return dfs(x+1,i-1)*dfs(i+1,y);
	}
	return 1;
}
int main()
{
	scanf("%lld",&n);
	cin>>s;
	s=" "+s;
	m=s.size()-1;
	for(ll i=1;i<=n;i++)
		scanf("%lf",&a[i]);
	for(ll i=1;i<=m;i++)
		if(s[i]=='(')q.push(i);
		else if(s[i]==')')
		{
			f[q.top()]=i;
			q.pop();
		}
	printf("%.4f",dfs(1,m));
}