自动搬运

查看原文

来自洛谷，原作者为

	龙·海流 我很懒，什么也没有留下

搬运于2025-08-24 21:36:37，当前版本为作者最后更新于2019-03-09 17:12:24，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

由于不会用洛谷的表格，所以之前写的题解看起来比较呲毛，在即将退役之际，用图床优化了一下外观。。。（真的退役了，闭关虽云乐，不如早早滚回去学文化课。。。）

这道题，如果考虑暴力的话，肯定会炸...

只能对公式**max{Vi; Vj}×|Xi − Xj |**进行优化

对于max，很容易想到sort将vi从小到大排序。。。

然后，优化绝对值的漫漫征程就此开始...

先研究一下样例 （sort后）

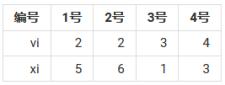
我们建立一个坐标轴，安置一下各位奶牛

先把第一头放进去

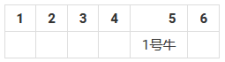
此时他周围没有牛，不发声

接着是第二头

2号牛前面有一头牛，于是发出声音2*（6-5）

然后是第三头...

在3号后面有两头牛，发出声音3*（5-1+6-1）也就是3*（5+6-1*2）（但愿你会想到什么）

最后是第四头

4号前有一头牛，后有两头牛，于是发出声音3*（3-1）+3*（5+6-3*2）

样例讲完了...

这时思路就出来了，我们把牛一头又一头地放入坐标系，每次放进去都算一次他与其他所有放进去的牛的声音，最后把每次放入求出的值加起来就是答案

或许你会发现，第i头牛和其他的牛发出的声音就等于=第i头牛的vi*（它之前牛的数目它的坐标-它之前所有牛的坐标和）+vi（它之后所有牛的坐标和-它之后牛的数目*他的坐标），对于牛的数目和牛的坐标，我们都可以用树状数组来维护一下...

如果你不明白为什么树状数组能维护，那我就拿牛的坐标来举一个例子...

以样例为例，开一个和坐标轴等长的树状数组，加入1号（插入位置为1号的横坐标，值为1），此时sum[maxx]=1,加入2号，sum[maxx]=2,二号之前于是有sum[5]头牛，之后有sum[maxx]-sum[6]头牛，加入三号，它之前有sun[0]头牛，之后有sum[maxx]-sum[1]头牛，以此类推...

一定开long long ！！！

切记切记

代码如下

#include<iostream>
#include<cstdio>
#include<algorithm>
using namespace std;
long long wz[20010],yy[20010],n,mn=20000;
long long ans;
long long read()
{	
    long long xx=0;
    char ch=getchar();
    while(ch<'0'||ch>'9') ch=getchar();
    while(ch>='0'&&ch<='9')
    {
     	xx=xx*10+ch-'0';
     	ch=getchar();
    }
    return xx;
}
struct node{
    long long xi;
    long long vi;
}a[20010];
bool cmp(node x,node y)
{
   	return x.vi<y.vi;
}
int lobit(int x) {	return x&(-x);}
void crwz(int x) { for(;x<=mn;x+=lobit(x)) wz[x]++;}
int z(int x)
{
    int sum=0;
    for(;x>=1;x-=lobit(x)) sum+=wz[x];
    return sum;
}
void cryy(int x,int v) { for(;x<=mn;x+=lobit(x)) yy[x]+=v;}
int y(int x)
{
    int sum=0;
    for(;x>=1;x-=lobit(x)) sum+=yy[x];
    return sum;
}
int jdz(int x)
{
    if(x<0) return -x;
    else return x;
}
int main()
{
    n=read();
    for(int i=1;i<=n;++i) a[i].vi=read(),a[i].xi=read();
    sort(a+1,a+1+n,cmp);
    for(int i=1;i<=n;++i)
    {
        int j=a[i].xi;
        ans+=a[i].vi*(z(j-1)*j-y(j-1)+y(mn)-y(j)-(z(mn)-z(j))*j);
        crwz(a[i].xi);
        cryy(j,a[i].xi);
    }
    printf("%lld",ans);
    return 0;
}

谢谢观看！！！