自动搬运

查看原文

来自洛谷，原作者为

	Soulist 再见了

搬运于2025-08-24 21:34:39，当前版本为作者最后更新于2018-07-19 12:15:17，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

关于本题

由于作者比较蒟蒻，所以做这道题的时候调试了非常之久......然后被卡常了？？？

反正由于常数问题，最后不得不将cin改为快读，才在400ms的时差下惊险通过此题。。。

因为本题题解大部分都看不懂，所以特意写一篇来让大家理解

关于做法

本题因为树的坐标均为给定的， 而查询比较多， 所以考虑使用2维前缀和QAQ， 对于每一个点我们都建立一个$S_{i,j}$表示以($0$,$0$)为左下坐标，($i$,$j$)为右上坐标的矩阵内部有多少课树。

那么对于每一个查询左下为点($a$, $b$)，右上为点($c$, $d$)的矩阵的查询，可以将之进行拆分。如下图：

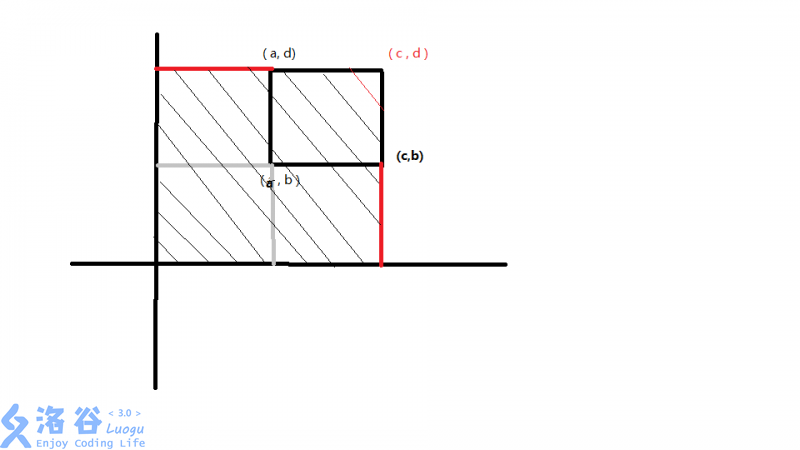
则图中的黑色部分为整个大的黑色部分也就是S_{c,d}减去旁边两个红色边所（自行想象一下）形成的矩形，也就是 $S_{a,d}$和 $S_{c,b}$ ; 注意到图中灰边矩形被减去了两次，所以还应当被加上上一次，所以有：黑色矩形中的树的数量为下式：

黑色矩形 $=$ $S_{c,d}$ + $S_{a-1,b-1}$- $S_{a-1,d}$-$S_{c,b-1}$

(自行想一想为什么是$a$ - $1$和$b$ - $1$)

(上面那一串话比较拗口搞不懂的话，其实您可以考虑画一张类似的如上的图，然后根据$S_{i,j}$的定义来手动模拟一下上式的计算过程)

所以目前的问题就转化成为了求出上述的2维前缀和了。

但由于本题数据范围过大，所以直接使用二维前缀和肯定是会炸的（不仅仅是因为它是$2$维，还有因为这里的前缀和对应的是题中坐标，而坐标过于广泛），所以考虑先对坐标进行离散化，然后对于所有的坐标（包括询问坐标）按照$x$轴进行排序，

按照$x$坐标排序后，我们进行前缀和操作的时候就不需要考虑$x$坐标了，然后同时将$y$坐标离散化掉（我是用排序离散化掉y的）

Q1：为什么按$x$坐标排序后就不需要考虑$x$坐标了

A1:因为排序后一定有后面来的点的$x$坐标一定比前面所有的$x$坐标都大，故当这个点为询问时只需要判断比该点的$y$坐标小的点有多少个即可。

所以之后对于每一个按照$x$坐标顺序读入的树点，可以将之分为两类操作：

(1):加入一个树点

(2):询问比该点$y$坐标要小的点数量

介于上述两个操作，我们可以显然可以使用一个数据结构来操作。（树状数组这么短为什么不用它呢？）

所以，下面给出代码了：（直接抄是肯定不会对的啦。）

#include<bits/stdc++.h>
using namespace std;
const int N = 3000000 + 5;
const int M = 1e7 + 5;
int tree[N], n, m;
struct node
{
   int x, y, id, qs, ut;
}t[N];
int cnt;
int qy[N], ans[N];
//刘氏快读
#define Finline __inline__ __attribute__ ((always_inline))
Finline char get_char()
{
   static char buf[200000001], *p1 = buf, *p2 = buf + fread(buf, 1, 200000000, stdin);
   return p1 == p2 ? EOF : *p1 ++;
}
inline int read(){
   int num = 0;
   char c;
   while((c = get_char()) < 48);
   while(num = num * 10 + c - 48, (c = get_char()) >= 48);
   return num;
}
//以上均为刘氏快读优化 
bool cmp(node r1, node r2)
{
   if(r1.x == r2.x) 
   	if(r1.y == r2.y) return r1.qs <= r2.qs;//x,y均相同的情况下优先处理树点而不是询问点
   if(r1.x == r2.x)
   	return r1.y < r2.y;//x相同则按y排序
   return r1.x < r2.x ; 
}
int lowbit(int x)//树状数组
{	
   return x&(-x);
}
int find1(int x)// 2分查找找出离散化后的y
{
   int l = 1, r = cnt;
   while(l < r)
   {
   	int mid = (l + r) / 2;
   	if(qy[mid] < x)
   		l = mid + 1;
   	else
   		r = mid - 1;
   }
   return l;
}//考虑优化find1？？？不知道怎么优化啊QAQ？？？离散化？？？ 
void add(int root, int rx, int ry, int rq)
{
   cnt++;
   t[cnt].x = rx;
   t[cnt].y = ry;
   t[cnt].id = root;
   t[cnt].qs = rq;
   qy[cnt] = ry;
}//加入一个点
void add_tree(int root, int k)//树状数组加入点
{
   for(int i = root; i <= cnt; i += lowbit(i))//从编号开始，每次向上依次传值。。。 
   	tree[i] += k;
}
int find(int root)查找比该点y小的点有多少个
{
   int num = 0;
   for(int i = root; i != 0; i -= lowbit(i))
   	num += tree[i];//从节点x开始，依次找到下路 
   return num;
}
void q_read()
{
   int p;
   n = read();
   m = read();
   int sx, sy;
   for(int i = 1; i <= n; i++)
   {
   	sx = read(); sy = read();
   	add(i, sx, sy, 0);//读入 
   }
   int a, b, c, d;
   for(int i = 1; i <= m; i++)
   {
   	a = read(); b = read(); c = read(); d = read();
   	p = m ;
   	add(i, a - 1, b - 1, 1);//0,1表示这个数是否为问题 
   	add(i + p, c, d, 1);
   	add(i + 2 * p, a - 1, d, 1);
   	add(i + 3 * p, c, b - 1, 1);
   }
}
void doit()
{
   sort(t + 1, t + cnt + 1, cmp);//通过关于x的排序离散化掉x
   sort(qy + 1, qy + cnt + 1);//通过关于y的排序离散化掉y
   for(int i = 1; i <= cnt; i++)
   {
   	int tof = find1(t[i].y);//查找值为t[i].y的坐标的点在离散化后的y序列中的位置
   	if(t[i].qs == 0)//是树点
   		add_tree(tof, 1);//加入一个点
   	else//是询问
   		ans[t[i].id]+=find(tof);//记录答案
   }
}
int qans(int x)
{
   int p = m ;
   return ans[x] + ans[x + p] - ans[x + 2 * p] - ans[x + 3 * p];//之前讲的前缀和，把最后一个1 * p改为3 * p即可A了
}
void write()//输出程序
{
   for(int i = 1; i <= m; i++)
   	cout << qans(i) <<endl;
}
//以下是优美的主程序 
int main()
{
   q_read();
   doit();
   write();
   return 1;//防止抄袭
}