自动搬运

查看原文

来自洛谷，原作者为

	GossWandering 千万里，风流去；我想哭，我想你。

搬运于2025-08-24 21:32:51，当前版本为作者最后更新于2020-03-28 20:12:36，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

---

• $\text{Update by Curry on 2020/12/1}$ : 修了图 & $\LaTeX$，更新了一点内容
• $\text{Update by Curry on 2021/3/12}$ : 感谢 $\color{black}\text{f}\color{red}\text{gtl}$ 神仙的提醒，修改了一个小错误。

题意大概是说 $n\times m$ 的矩形中找到一个边长为 $c$ 的矩形使它的价值最大。

根据题意，我们可以枚举左上角的坐标，利用边长 $c$ 算出左下、右上、右下角。再暴力枚举价值和，更新答案即可。

时间复杂度：$O(nmc^2)$

预计得分：50~70 points

程序如下：

#include <bits/stdc++.h>
#define inf 0x3f3f3f3f
using namespace std;
const int N=1010;

int n,m,c;
int val[N][N],maxx=-inf,wherex,wherey;

int main(){
    scanf("%d%d%d",&n,&m,&c);
    for(int i=1; i<=n; i++)
        for(int j=1; j<=m; j++)
            scanf("%d",&val[i][j]); //输入
    for(int x1=1; x1<=n-c+1; x1++) 
        for(int y1=1; y1<=m-c+1; y1++){  //枚举左上角
            int x2=x1+c-1;
            int y2=y1+c-1;  //计算右下角
            int ans=0;
            for(int i=x1; i<=x2; i++)
                for(int j=y1; j<=y2; j++)
                    ans += val[i][j];
            if(ans>maxx){
                maxx=ans;
                wherex=x1;
                wherey=y1;
            }//更新答案
        }
    printf("%d %d",wherex,wherey);
    return 0;
}

提交上去？？啊，果然70分。沮丧的我们不得不思考优化。

在此之前，我们思考，我们写出的程序到底差在哪儿？？？

请先思考，再往下阅读

原来，我们的程序有些地方算重复了：

$\text{for example}$:

• $(1,1)$ 为左上角，$c=2$ 时我们算了$(1,1)+(1,2)+(2,1)+(2,2)$；
• $(1,2)$ 为左上角，$c=2$ 时我们算了$(1,2)+(1,3)+(2,2)+(2,3)$；

咦？$(1,2)+(2,2)$ 被我们算重了！对于这种情况，有一个经典的解决方法——预处理。

所以我们考虑用（二维）前缀和优化

下面我们讲一下什么是二维前缀和，建立在一维前缀和之上，我们要求一个矩阵内一个任意的子矩阵的数的和，我们就可以用二维前缀和，我们还是用DP来预处理，状态和一维前缀和差不多，只不过我们多加了一维。

用 $f(i,j)$ 表示 $1,1$ 这个点与 $(i,j)$ 这个点两个点分别为左上角和右下角所组成的矩阵内的数的和，则状态转移方程为：

$f(i,j)=f(i,j-1)+f(i-1,j)-f(i-1,j-1)+val_{i,j}$

其中 $val_{i,j}$ 表示 $(i,j)$ 这一格的价值。

怎么来的呢？我们画一下图就知道了。

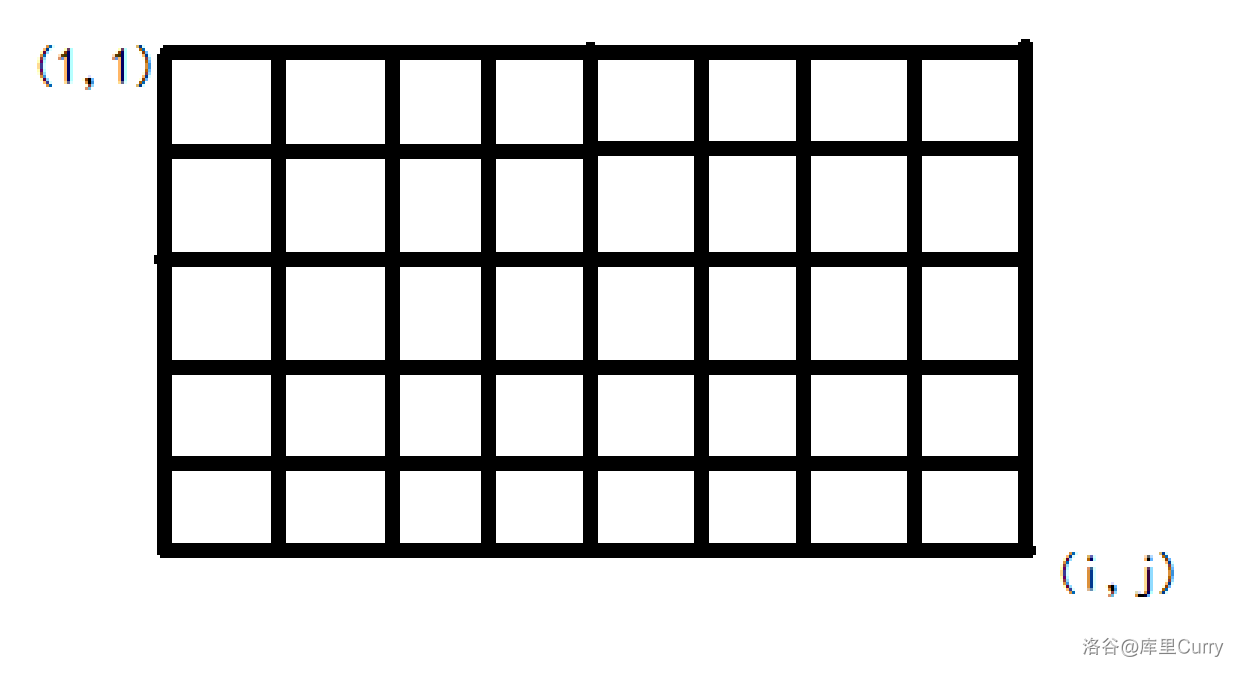
一开始是这样的：$f(i,j)$ 为 $0$，即图中所有格子都是白色的。

回顾转移方程：$f(i,j)=f(i,j-1)+f(i-1,j)-f(i-1,j-1)+val_{i,j}$

第一个加的是 $f(i,j-1)$，所以我们将 $(1,1)$ ~ $(i,j-1)$ 染成黄色，表示加过一次。如上图所示。

此后再加上 $f(i-1,j)$，但是我们发现两次染色中有一部分是重复染色的。即：$(1,1)$~$(i-1,j-1)$，它们被染过两次色，在上图中我们将这一块区域染成棕色。

既然重复计算了，那我们就剪掉，即减去$f(i-1,j-1)$，此时 $(1,1)$~$(i-1,j-1)$ 又回归了黄色（即只染过一次色）。我们发现：只需再把 $(i,j)$ 这一格染成黄色，便大功告成了！

即加上：$val_{i,j}$，如下图：

所以我们用图解证明了转移方程 $f(i,j)=f(i,j-1)+f(i-1,j)-f(i-1,j-1)+val_{i,j}$

我们看一下实现代码：

for(int i=1; i<=m; i++)
    for(int j=1; j<=n; j++)
        f[i][j]=val[i][j]+f[i-1][j]+f[i][j-1]-f[i-1][j-1];

现在只需枚举左上角，根据边长 $c$ 算出左下角，然后用二维前缀和 $O(1)$ 更新。

附 $(x_1,y_1)$ 到 $(x_2,y_2)$ 权值和的计算方法：

$f(x_2,y_2)-f(x_2,y_1-1)-f(x_1-1,y_2)+f(x_1-1,y_1-1)$

这可以用二维前缀和的定义进行理解，或用图解也行。

完整代码不提供了，其余几篇题解都讲的挺好。