自动搬运

查看原文

来自洛谷，原作者为

	System32 We shall never surrender!

搬运于2025-08-24 21:32:01，当前版本为作者最后更新于2025-01-23 14:30:10，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

这篇题解里有这样一段话：

4. 那这题是不是没做头了？

题当然还是可以做，你可以枚举棋盘上每一个点来判断是否为王与骑士相遇点，然后暴力枚举骑士，再暴力枚举集合点，最劣是 $O(R^3*C^3)$ ，但是不可能达到这么大。

但是实际上没有 $R \times C$ 这么多点（但是 $5 \times 5$ 和 $7 \times 7$ 很明显不够）。

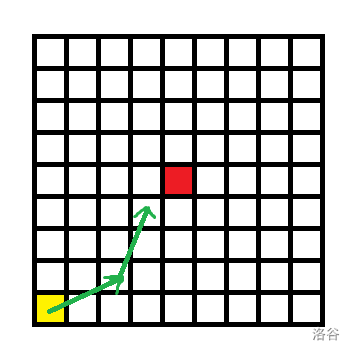
先考虑对角线的情况，图中红点是国王，黄点是骑士，绿色箭头是骑士的移动路线。

这段路线骑士走会产生 $4$ 的代价，但国王走只有 $3$ 的代价，由此可以得出上车点在对角线上时只能让国王走到上车点。

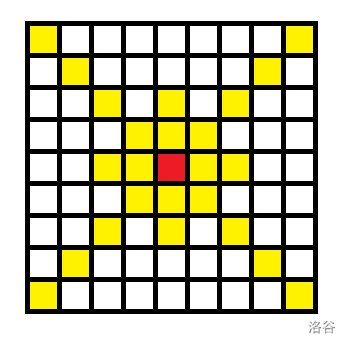
手玩一下这幅图（也可以写暴力来验证），可以得出结论：如果上车点在黄色点上，那么就一定会让国王走到上车点。

所以只需要把 $5 \times 5$ 的题解复制借鉴一下，把贪心范围加上国王所处的两条对角线就可以了。

最后时间复杂度为 $O((R + C) \times R^2 \times C^2)$，可以通过本题。

Code

#include <bits/stdc++.h>
using namespace std;

#define int long long

struct node {
	int x, y;
	int d;
} pe[2010];

int r, c, dx[] = {1, 2, 2, 1, -1, -2, -2, -1},  dy[] = {2, 1, -1, -2, -2, -1, 1, 2}, cnt;
bool v[50][30];
int ans = 1145141919810ll, d[50][30][50][30];

void bfs(int a, int b) {
	queue<node> q;
	q.push({a, b, 0});
	v[a][b] = 1;
	d[a][b][a][b] = 0;
	while (!q.empty()) {
		int x = q.front().x, y = q.front().y;
		d[a][b][x][y] = q.front().d;
		q.pop();
		for (int i = 0; i < 8; i++) {
			int nx = x + dx[i], ny = y + dy[i];
			if (nx >= 1 && nx <= r && ny >= 1 && ny <= c && !v[nx][ny]) {
				v[nx][ny] = 1;
				q.push({nx, ny, d[a][b][x][y] + 1});
			}
		}
	}
}

signed main() {
	cin >> r >> c;
	for (int i = 0; i <= r + 1; i++) {
		for (int j = 0; j <= c + 1; j++) {
			for (int a = 0; a <= r + 1; a++) {
				for (int b = 0; b <= c + 1; b++) {
					d[i][j][a][b] = 2e8;
				}
			}
		}
	}
	char t1;
	int t2;
	while (cin >> t1 >> t2) {
		pe[cnt].x = t2;
		pe[cnt].y = t1 - 'A' + 1;
		cnt++;
	}
	cnt--;
	for (int i = 1; i <= r; i++) {
		for (int j = 1; j <= c; j++) {
			memset(v, 0, sizeof(v));
			bfs(i, j);
		}
	}
	for (int i = 1; i <= r; i++) {
		for (int j = 1; j <= c; j++) {
			int g = 0;
			for (int k = 1; k <= cnt; k++) {
				g += d[pe[k].x][pe[k].y][i][j];
			}
			ans = min(g + max(abs(pe[0].x - i), abs(pe[0].y - j)), ans);
			for (int k = 1; k <= cnt; k++) {
				int temp = g - d[pe[k].x][pe[k].y][i][j];
				for (int a = max(1ll, pe[0].x - 2); a <= min(r, pe[0].x + 2); a++) {
					for (int b = max(1ll, pe[0].y - 2); b <= min(c, pe[0].y + 2); b++) {
						ans = min(temp + d[pe[k].x][pe[k].y][a][b] + max(abs(a - pe[0].x), abs(b - pe[0].y)) + d[a][b][i][j], ans);
					}
				}
				int a = pe[0].x, b = pe[0].y;
				while (a > 0 && b > 0) {
					a--;
					b--;
					ans = min(temp + d[pe[k].x][pe[k].y][a][b] + max(abs(a - pe[0].x), abs(b - pe[0].y)) + d[a][b][i][j], ans);
				}
				a = pe[0].x, b = pe[0].y;
				while (a > 0 && b <= c) {
					a--;
					b++;
					ans = min(temp + d[pe[k].x][pe[k].y][a][b] + max(abs(a - pe[0].x), abs(b - pe[0].y)) + d[a][b][i][j], ans);
				}
				a = pe[0].x, b = pe[0].y;
				while (a <= r && b > 0) {
					a++;
					b--;
					ans = min(temp + d[pe[k].x][pe[k].y][a][b] + max(abs(a - pe[0].x), abs(b - pe[0].y)) + d[a][b][i][j], ans);
				}
				a = pe[0].x, b = pe[0].y;
				while (a <= r && b <= c) {
					a++;
					b++;
					ans = min(temp + d[pe[k].x][pe[k].y][a][b] + max(abs(a - pe[0].x), abs(b - pe[0].y)) + d[a][b][i][j], ans);
				}
			}
		}
	}
	cout << ans << endl;
	return 0;
}