自动搬运

查看原文

来自洛谷，原作者为

	Huami360 菜是原罪

搬运于2025-08-24 21:27:42，当前版本为作者最后更新于2018-09-18 14:57:54，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

不知道为什么$O(n^4)$的玄学方法能过，正解显然是$O(n^2)$的，枚举对角线，然后算出另外两点判断存不存在。

关键就在怎么通过对角线算出另外两点的坐标。

先贴公式。

int midx = (x[i] + x[j]) / 2;
int midy = (y[i] + y[j]) / 2;            
int x1 = midx - (midy - y[i]), y1 = midy + (midx - x[i]);
int x2 = midx + (midy - y[i]), y2 = midy - (midx - x[i]);

$(x[i],y[i]),(x[j],y[j])$是对角线的两个点，

$(x1,y1),(x2,y2)$是我们算出来的另两个点的坐标。

怎么来的呢？

如图，

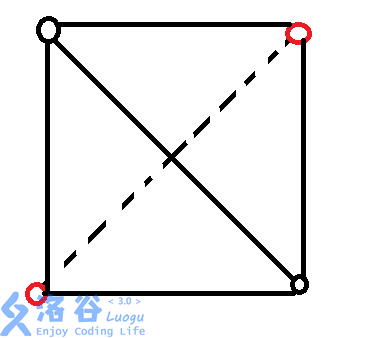
黑点是我们枚举的对角线，红点就是我们要算的另外两点。

我们算出对角线的重点$(midx,midy)$。

然后做几条辅助线，如图：

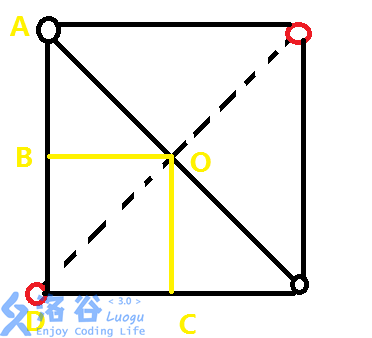
图中的$OC$,$OB$是垂直于$x$轴和$y$轴，并不一定垂直于正方形的边。

易得△$ABO$ ≌ △$DCO$，于是，这两个三角形以$AB$,$CD$为底的高也相等，现在是不是就能理解这个公式了。

贴代码$O(n^2)$常数小

#include <cstdio>
#define Open(s) freopen(s".in","r",stdin);freopen(s".out","w",stdout);
#define Close fclose(stdin);fclose(stdout);
int n, ans;
int x[60000], y[60000], vis[1100][1100], xs[1100][1100];
int main(){
	Open("count");
	scanf("%d", &n);
	for(int i = 1; i <= n; ++i){
		scanf("%d%d", &x[i], &y[i]);
		x[i] = (x[i] + 51) << 1; //防止负数和小数
		y[i] = (y[i] + 51) << 1;
		vis[x[i]][y[i]] = 1;
	}
	for(int i = 1; i < n; ++i)
		for(int j = i + 1; j <= n; ++j){
            int midx = (x[i] + x[j]) / 2;
            int midy = (y[i] + y[j]) / 2;            
            int x1 = midx - (midy - y[i]), y1 = midy + (midx - x[i]);
            int x2 = midx + (midy - y[i]), y2 = midy - (midx - x[i]);
            if(x1 <= 0) continue; if(x2 <= 0) continue;
            if(y1 <= 0) continue; if(y2 <= 0) continue; 
            if(vis[x1][y1] && vis[x2][y2]) ++ans;
        }
	printf("%d\n", ans >> 1);
	return 0;
}