自动搬运

查看原文

来自洛谷，原作者为

	enceladus ？

搬运于2025-08-24 21:27:19，当前版本为作者最后更新于2018-09-06 15:45:44，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

只有两篇题解，那窝来水一篇题解QAQ。

安利博客

题目传送门

先说一下我犯得一个严重错误。题目没读清。让输出移动k个点的，而不是n个。一定要

认真读题

啊。

这个题是暴力枚举，可是，为什么可以。

下面让我们想一下这个；

则需要的代价为|x0-x1|+|y0-y1|。求使得K(K=1,…,N)个点在同一位置上最少需要的代价。

最优的点的横纵坐标一定来源于已知点的横纵坐标

为什么这么说呢，联想两点之间线段最短，如果有两个点，把它们移动到一个点上，最优解是移动到他两个连线的线段上。

比方说下面的图

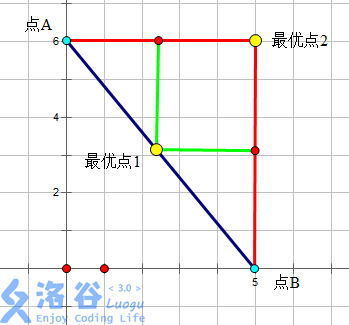
1是一个最优点，而根据曼哈顿距离的计算公式，我们可以发现，最优点2与最优点1是等效的。

我们考虑找到每两个点的最优点，这些点的最优点又会在最优点连城的线段上。

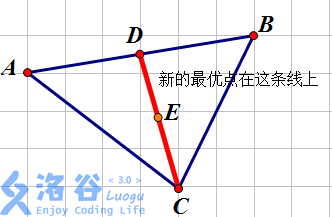
而这个点，又可以经过转化，转到一个横纵坐标已知的点上。

而且就算是多边形也没有关系啊。

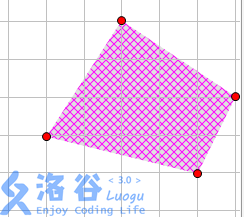
最优点一定在网格区域内，网格区域的点又可以转化位已知的点的横纵坐标。

现在就证明了枚举横纵坐标的 正确性 了

下面还有有一个要注意的点。本人的最大值付为了0x7fffff； 然后

看看这个QAQ

${\Huge\color{Salmon}{Make-sure-your-maximum-is-the-maximum}}$

付成0x7fffffff就可以了。

${\color{Green}{By}}$

${\color{Green}{enceladus}}$

最后献上本人丑陋的代码,(代码有锅，勿抄，不要变棕啊）

#include<iostream>
#include<cstdio>
#include<cmath>
#include<algorithm>
#define INF 0x7fffffff
#define ll long long
#define IL inline
#define R register
using namespace std;
ll ans[57];
int x[57],y[57];
long long l[57];
ll tot=0;
int mx,my; 
int n;

int main()
{
    cin>>n;
    for(int i=1;i<=n;i++)
    {
    	cin>>x[i]>>y[i];
        ans[i]=0x7fffffff;
    }  
	    for(int j=1;j<=n;j++)
		{
			for(int k=1;k<=n;k++)
			{
			    for(int t=1;t<=n;t++) 
			    {
			    	l[t]=abs(x[t]-x[j])+abs(y[t]-y[k]);
				}
				tot=0;
				sort(l+1,l+1+n);
			    for(int i=1;i<=n;i++) 
				{
				    tot+=l[i];
				    ans[i]=min(ans[i],tot); 
			    }
			}	
		} 
	for(int i=1;i<=n;i++)
	{
		cout<<ans[i]<<endl;
	}
	return 0;
}