自动搬运

查看原文

来自洛谷，原作者为

	JRzyh Back.

搬运于2025-08-24 21:26:11，当前版本为作者最后更新于2021-08-21 13:00:24，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

---

从基础开始讲解记忆化搜索。

$\texttt{Part~-1~前置知识}$

深度优先搜索（dfs）。

$\texttt{Part~0~开始之前}$

拿到 P1535 这题的第一反应就应该是搜索。

这题爆搜思路很好想。

首先从出发点开始搜，

向上下左右四个方向搜索。

那么就只要到达目的地 ans++。

const int dx[4]={1,-1,0,0};
const int dy[4]={0,0,1,-1};
int n,m,t,r1,c1,r2,c2,ans;
bitset<108>b[108];
void dfs(int x,int y,int time)
{
	if(time>t)return ;
	if(time==t)
	{
		if(x==r2&&y==c2)
		{
			ans++;
			return ;
		}
		else return ;
	}
	for(int i=0;i<4;i++)
	{
		if(b[x+dx[i]][y+dy[i]]||x+dx[i]<1||x+dx[i]>n||y+dy[i]<1||y+dy[i]>m)continue;
		dfs(x+dx[i],y+dy[i],time+1);
	}
}
int main()
{
	cin>>n>>m>>t;
	for(int i=1;i<=n;i++)
	{
		string s;
		cin>>s;
		for(int j=0;j<m;j++)
		{
			if(s[j]=='*')b[i][j+1]=1;
		}
	}
	cin>>r1>>c1>>r2>>c2;
	dfs(r1,c1,0);
	cout<<ans<<endl;
 	return 0;
}

但肯定是过不了的，现在开始记忆化。

$\texttt{Part~1~记忆化是啥}$

记忆化搜索，就是把已经搜到的状态开个数组记录下来，再次搜的时候直接返回。

举个例子：dfs 求斐波那契数列。

众所周知：

$$F_n = \left\{\begin{aligned} 1 \space (n \le 2) \\ F_{n-1}+F_{n-2} \space (n\ge 3) \end{aligned}\right. $$

所以很好写：

int f(int n)
{
   if(n<=2)return 1;
   else return f(n-1)+f(n-2);
}

现在调用 f(5) 看看搜索树是怎样的：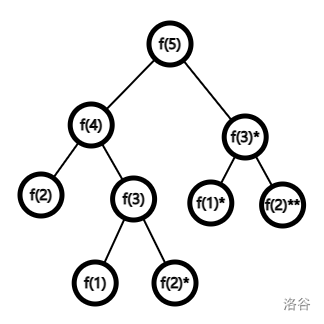

发现了什么：

相同函数有多次重复调用，这个计算花的时间就是浪费的。

可以怎么办呢？

记忆化呀。

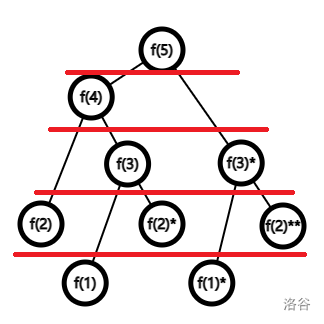
开一个数组 re[]={0} 记录下来搜过的状态。

int f(int n)
{
   if(re[n]!=0)return re[n];
   if(n<=2)return re[n]=1;//等价于 re[n]=1;return re[n]; 下同。
   else return re[n]=f(n-1)+f(n-2);
}

这样搜索树就会好多了：

$\texttt{Part~2~记忆化咋写}$

把上面的 dfs 扒下来：

void dfs(int x,int y,int time)
{
	if(time>t)return ;
	if(time==t)
	{
		if(x==r2&&y==c2)
		{
			ans++;
			return ;
		}
		else return ;
	}
	for(int i=0;i<4;i++)
	{
		if(b[x+dx[i]][y+dy[i]]||x+dx[i]<1||x+dx[i]>n||y+dy[i]<1||y+dy[i]>m)continue;
		dfs(x+dx[i],y+dy[i],time+1);
	}
}

注意到 dfs 是 void 类型的，借助全局变量统计答案。把它改成另一种写法：int 型，用返回值返回答案。

int dfs(int x,int y,int time)
{
	if(time>t)return 0;
	if(time==t)
	{
		if(x==r2&&y==c2)return 1;
		else return 0;
	}
	int ans=0;
	for(int i=0;i<4;i++)
	{
		if(b[x+dx[i]][y+dy[i]]||x+dx[i]<1||x+dx[i]>n||y+dy[i]<1||y+dy[i]>m)continue;
		ans+=dfs(x+dx[i],y+dy[i],time+1);
	}
	return ans;
}

然后定义一个记忆化数组 re[x][y][t]，初始值都为 $-1$。

表示 dfs(x,y,t) 的值，也就是花了 $t$ 秒走到 $(x,y)$ 的方案数。

搜的时候加入发现搜过就直接返回。

if(re[x][y][time]!=-1)return re[x][y][time];

然后再每个 dfs 算出答案的时候记录即可。

code:

int dfs(int x,int y,int time)
{
	if(re[x][y][time]!=-1)return re[x][y][time];
	if(abs(x-r2)+abs(y-c2)>t-time)return re[x][y][time]=0;
	if(time>t)return re[x][y][time]=0;
	if(time==t)
	{
		if(x==r2&&y==c2)return re[x][y][time]=1;
		else return re[x][y][time]=0;
	}
	int ans=0;
	for(int i=0;i<4;i++)
	{
		if(b[x+dx[i]][y+dy[i]]||x+dx[i]<1||x+dx[i]>n||y+dy[i]<1||y+dy[i]>m)continue;
		ans+=dfs(x+dx[i],y+dy[i],time+1);
	}
	return re[x][y][time]=ans;
}

别走，还没结束。还没点赞呢。

$\texttt{Part~3~复杂度分析}$

dfs 复杂度 $=$ 节点个数 $\times$ 一次递归复杂度。

一次递归复杂度是 $O(1)$。

因为每个 re[x][y][t] 至多计算一次，所以节点个数是 $O(nmt)$。

复杂度 $O(nmt)$。

但假如不记忆化，

一次递归复杂度还是 $O(1)$。

但因为没有记忆化，节点个是深为 $t$ 的满 $4$ 叉树 $=\dfrac{(4^t-1)}{3}$ 也就是 $O(4^t)$ 。

记忆化还是很有用的。

$\texttt{Part~4~code}$

////////////////////////
///////////////////////
//////////////////////
/////////////////////
/////Author/////////
//////zyh//////////
//////////////////
/////////////////
////////////////
///////////////
//////////////
/////////////
////////////
#include<bits/stdc++.h>
#define EL putchar('\n')
#define SP putchar(' ')
using namespace std;
const int dx[4]={1,-1,0,0};
const int dy[4]={0,0,1,-1};
int n,m,t,r1,c1,r2,c2;
bitset<108>b[108];
int re[108][108][20];
int dfs(int x,int y,int time)
{
	if(re[x][y][time]!=-1)return re[x][y][time];
	if(abs(x-r2)+abs(y-c2)>t-time)return re[x][y][time]=0;
	if(time>t)return re[x][y][time]=0;
	if(time==t)
	{
		if(x==r2&&y==c2)return re[x][y][time]=1;
		else return re[x][y][time]=0;
	}
	int ans=0;
	for(int i=0;i<4;i++)
	{
		if(b[x+dx[i]][y+dy[i]]||x+dx[i]<1||x+dx[i]>n||y+dy[i]<1||y+dy[i]>m)continue;
		ans+=dfs(x+dx[i],y+dy[i],time+1);
	}
	return re[x][y][time]=ans;
}
int main()
{
	cin>>n>>m>>t;
	memset(re,-1,sizeof(re));
	for(int i=1;i<=n;i++)
	{
		string s;
		cin>>s;
		for(int j=0;j<m;j++)
		{
			if(s[j]=='*')b[i][j+1]=1;
		}
	}
	cin>>r1>>c1>>r2>>c2;
	cout<<dfs(r1,c1,0)<<endl;
 	return 0;
}

$\texttt{Part~5~一些后话}$

其实记忆化和 dp 是有亿点点像的。

求赞 。