自动搬运

查看原文

来自洛谷，原作者为

	ctq1999 今晚はの月が綺麗ですね

搬运于2025-08-24 21:25:56，当前版本为作者最后更新于2019-10-27 12:16:37，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

传送门

这题有个证明比较难想（其他题解都没看懂），其他还好。

题面简述

有一个矩形。矩形上的格子有不同高度。你可以在第一行（x = 1）的任意多个格子放水，水会沿低的格子一直落下来。

要求能否使最后一行（x = n）所有格子有水。

思路

前置知识： 搜索

对于水流的过程的搜索就不多阐述了

对于最后一行没有标记的格子直接统计并输出即可

对于有解（最后一行全部覆盖）的最少统计：

经过思考可以发现一个水流到最后一行的覆盖必是一个连续的线段

证明：

前提：有解

假设有一条水流是这样的

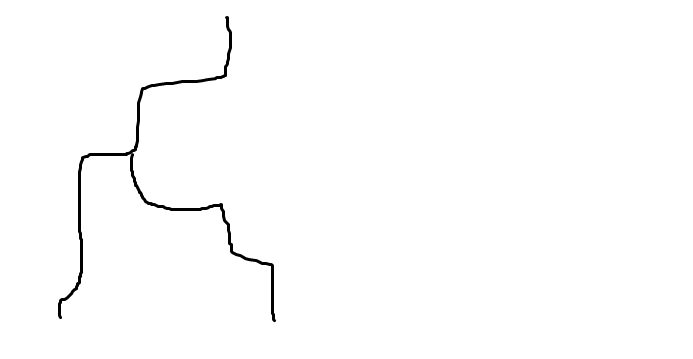
若有解，则必定有另一条水流流到图中蓝色区域

则棕线（第二条水流）必与黑线有交点

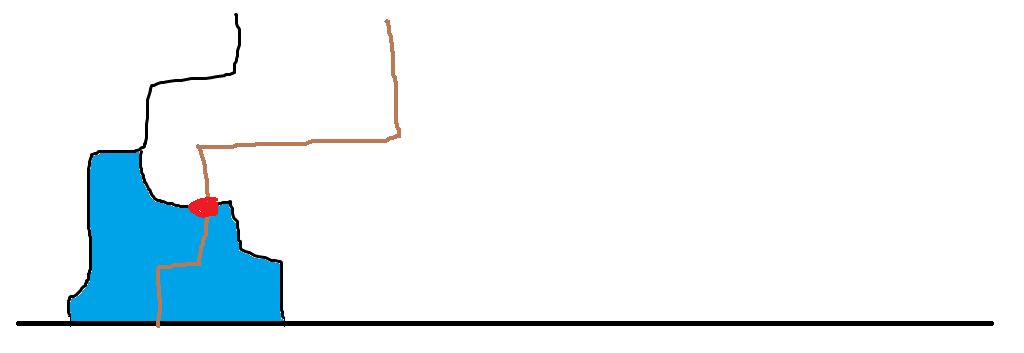
棕线流到蓝色区域，黑线也可从红点处流入蓝色区域

与假设矛盾，所以有解时，一条水流必定有连续区间

再不懂看这个

你的水流可以长这样（蓝色是不能流到的区域）

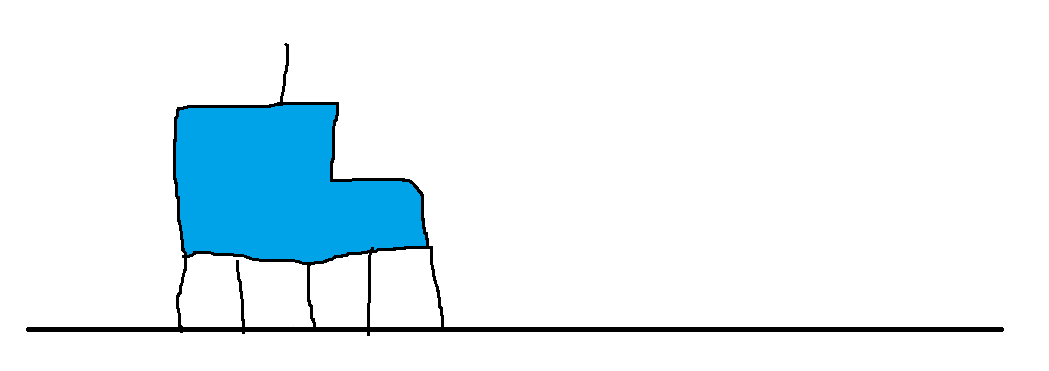
但这样的话

别的水一定流过不去了呀（否则它自己也过去了），所以这样一定无解

于是我们可以在最后一行贪心，从(n, 1)开始，不断找一个左端点在上一个右端点之内，右端点最远的区间。不要说着说着忘记统计区间了（笑

更多细节看程序

懂的话尽量自己写，否则没什么收获的

#include <bits/stdc++.h>

#define MAXN 1010

using namespace std;

int n, m;

int dx[] = {-1, 0, 1, 0};
int dy[] = {0, 1, 0, -1};//方向数组 方便搜 

int vis[MAXN][MAXN];

int h[MAXN][MAXN], l[MAXN][MAXN], r[MAXN][MAXN];

void dfs(int x, int y) {
	vis[x][y] = 1;
	for (int i = 0; i < 4; i++) {
		int x1 = x + dx[i];
		int y1 = y + dy[i];
		if (x1 < 1 || x1 > n || y1 < 1 || y1 > m || h[x][y] <= h[x1][y1]) continue;
		if (!vis[x1][y1]) dfs(x1, y1);
		//注意  若(x1, y1)格子已经过就不用搜了
		//但    l和r还是要更新的 
		l[x][y] = min(l[x][y], l[x1][y1]);
		r[x][y] = max(r[x][y], r[x1][y1]);
	}
}

int main() {
	scanf("%d%d", &n, &m);
	memset(l, 21000000, sizeof(l));
	
	for (int i = 1; i <= n; i++) {
		for (int j = 1; j <= m; j++) {
			scanf("%d", &h[i][j]);
			if (i == n) l[i][j] = r[i][j] = j;//最后一行初始化 
		}
	}	
	
	for (int i = 1; i <= m; i++) {
		if (!vis[1][i]) dfs(1, i);//若这格已经搜过了就不用搜了 
	}
	
	bool check = true;
	int ans = 0;
	
	for (int i = 1; i <= m; i++) {
		if (!vis[n][i]) {
			check = false;
			ans++;		
		}
	}
	
	if (!check) {
		cout << 0 << endl << ans << endl;
		return 0;
	}
	
	int left = 1, right = r[1][1];
	
	//统计区间数 
	while (left <= m) {
		for (int i = 1; i <= m; i++) {
			if (l[1][i] <= left) {
				right = max(right, r[1][i]);
			}
		}
		
		left = right + 1;
		ans++;
	}
	
	cout << 1 << endl << ans << endl;
	return 0;
} 

日拱一卒，功不唐捐