自动搬运

查看原文

来自洛谷，原作者为

	狸狸养的敏敏 **

搬运于2025-08-24 21:25:04，当前版本为作者最后更新于2019-03-10 16:27:42，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

---

题意简述

给出一个$N$行的，第$i$行有$N＋1－i$个数的倒三角形，从其中选取$M$个数,选取条件为当前数的左上角和右上角必须被选取过才能选取，求选取的数字的最大和。

分析：

拿到题目首先找题目的特点，就是和别的题目不同的地方，这题的特点就是：每个数选取条件为左上和右上的数已选。

通常的思路，数从上往下取，那么这一层的某个数能不能取，只与上一层的数取不取有关。

极像数字三角形问题的变形。

比较容易想到了Dp，想到的状态表示法为$F[i,j,k]$表示第$(i,j)$个位置，已经选取了$k$个数字的最大值，转移自然是从左上角和右上角（在直角三角形中位正上方和右上方）转移过来。

问题：

1、如何判断左上角和右上角的状态能否转移到当前状态？即左上与右上都已经选取，则可转移；

2、如何转移呢？找不出方程。

原因：

本问题符合DP的子结构性质，却不符合DP的无后效性。

(以下关于无后效性的解释来自网络)

---

所谓无后效性原则，指的是这样一种性质：某阶段的状态一旦确定，则此后过程的演变不再受此前各状态及决策的影响。

也就是说，“未来与过去无关”，当前的状态是此前历史的一个完整总结，此前的历史只能通过当前的状态去影响过程未来的演变。

具体地说，如果一个问题被划分各个阶段之后，阶段$i$ 中的状态只能由阶段 $i+1$ 中的状态通过状态转移方程得来，与其他状态没有关系，特别是与未发生的状态没有关系，这就是无后效性。

---

对于$F[i,j,k]$ ，能否转移，与之前的方案是有关的。 即有后效性，为了消除后效性，通常和方法是加记一维，用二进制数表示上一行的选取情况。

这样，就没有后效性了。而且转移的方法也简单，直接判断上一行所需的两个数是否已经选取了。

然而，状态数为$N^2*2^N$，这个数量级在$N=50$的时侯是不可承受的。

看来这条思路已经山穷水尽了。只能回头从别的方面想了。题目中有否可用的信息呢？

转换思路

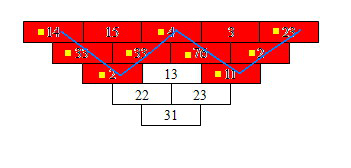
分析题目中的选取条件，我们会发现：

这道题最终解的形态（选中的数字）可以描述成若干个三角形相互连接或重叠，如上图中的红色砖块，由两个蓝色标识的三角形部分重叠而成。

将最终解的形态（选中的数字）的每列最下层点用线画出（图中的蓝线），可以发现：

1、构成的轮廓线是一条锯齿状的折线；
2、轮廓线上的相邻点布局在三角形的相列与相邻行上，即如果从左向右观察列，轮廓线上的点只能从其左列的上方行或下方行连过来；
3、轮廓线上点所在列的上方点一定全部被选中。

则把原问题转化为沟画出重叠三角形的锯齿状轮廓折线，找到一条合法的路径，使得围在轮廓线内的数字代价和最大。

另，根据第3点分析，轮廓线上点所在列的上方点一定全部被选中，可将选中的数字压缩到轮廓线上点，问题进一步转化为求轮廓线上点的代价和最大。

算法：

1、预处理：

设$cost[i,j]$表示选取第$i$行第$j$个，需要一起选取的其他点的个数。即与这个点同一列，且在这个点之上的点的个数。

2、

$sum[i,j]$表示选取第$i$行第$j$个，需要一起选取的其他点的数值和。即与这个点同一列，且在这个点之上的点的数值之和。

这样，cost[],sum[]分别记录了走到每个格子本列的数字个数与代价和。

3、

因为对于任意一列的任意一个数字，转移到它的前提与之前的方案无关，所以满足了Dp的无后效性。 同时当前列必定要由之前的某个最优状态转移过来，所以又满足了最优子结构的性质。故DP是可行的。

4、重新回到原来的状态表示：

记$F[i,j,k]$表示(i,j)这个点，已经选取了K个数字的最优值。

从左到右进行DP，一个点的最优值则由这个点左列上行的点或左列下行的点转移过来，因为轮廓线是连续的。

得到了Dp方程： $F[i,j,k]:=max(F[i-1,j,k-cost[i,j]],F[i+1,j-1,k-cost[i,j]])+sum[i,j] $

Tips:

要额外开一排0排，用来表示每一列一个都不取的情况。

End.