自动搬运

查看原文

来自洛谷，原作者为

	ARIS2_0 路虽远，行则将至；事虽难，做则必成。

搬运于2025-08-24 23:03:31，当前版本为作者最后更新于2024-09-06 18:00:12，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

（下文简称 Drifty 为 d，hgcnxn 为 h，放心，他们都是我同学，不会在意的……应该吧 （逃））

结论：

在图中找具有如下结构的节点 $x$ ，我们将这种节点命名为关键点。

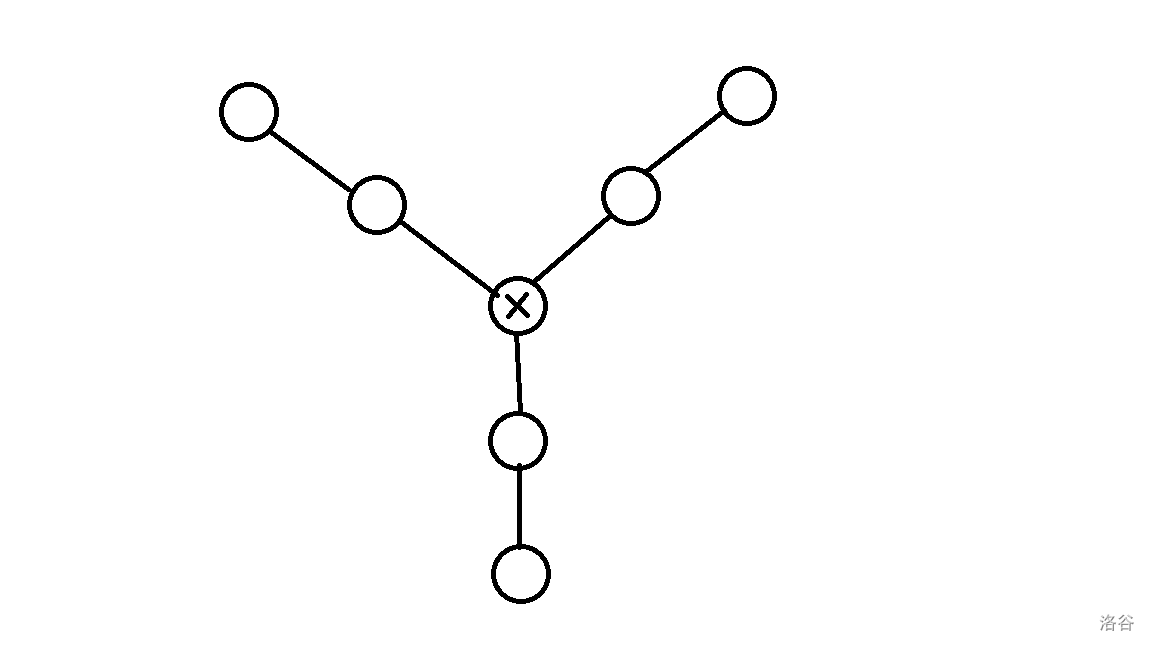
严谨地，满足以下条件的为关键点 $p$：

• $p$ 的入度不小于 $3$

• 与 $p$ 相连的节点中，至少有 $3$ 个节点的入度不小于 $2$。

对图跑一遍 BFS，得到 $d_i$ 与 $h_i$，分别代表 d 到点 $i$ 的距离与 h 到点 $i$ 的距离。最后，对于图中的每一个关键点，若有任何一个关键点 $p$ 满足 $d_p< h_p-1$ ，输出 Drifty，否则输出 hgcnxn。

下面给出证明。过程可能会有一点冗长而且不严谨，但相信我，我能把你讲懂，应该比官方题解好一点……吧？

证明：

让我们先理解题意。因为 h 的目标仅仅是捉到 d，并且还没有时间限制，所以 h 的最优方案一定是把整个图全跑一遍。那么，如果 d 能赢，他一定有方法和 h 玩“套圈子”。而本题给定的又是无向无环图，所以，我们要找到一个 d 可以与 h 玩“套圈子”的子图。那么，我们现在来开始寻找这个子图。

首先，子图显然不可能是一条链，这样 h 肯定能捉到 d；其次，子图如果是以下这种结构，也是不可能的：

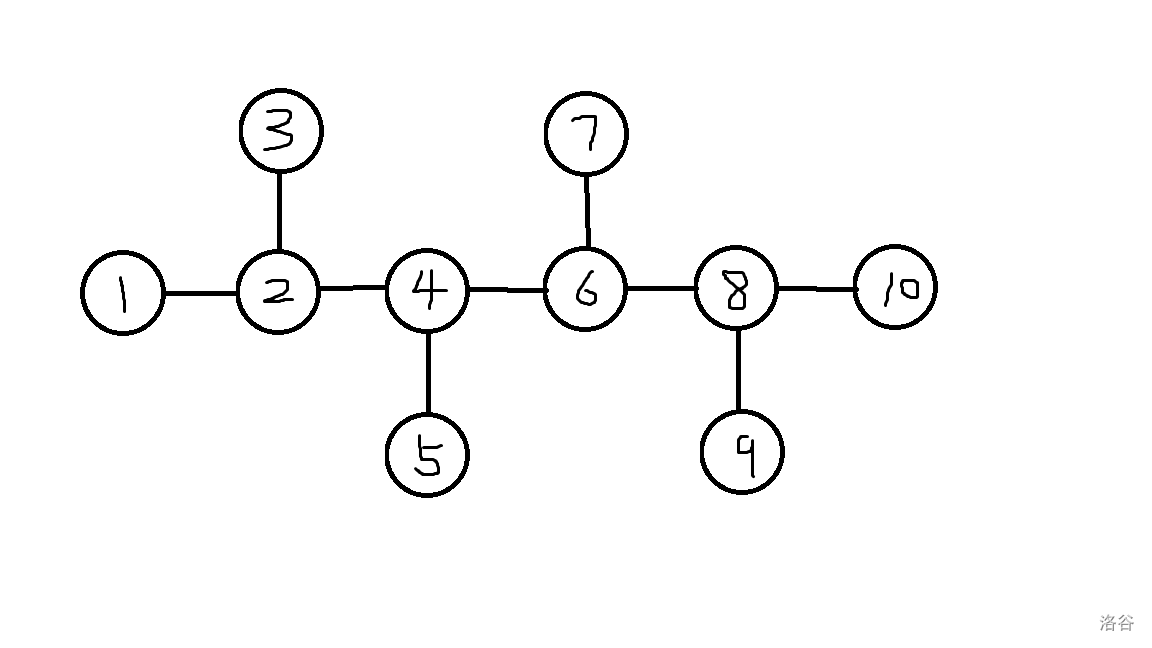
对于这样的结构，h 可以先到一号节点，然后按
1->2->3->2->4->5->4->6->7->6->8->9->8->10
的顺序搜，也总能找到 d。

那么，回收开头，开始证明：

对于图中的每一个关键点，若有任何一个关键点 $p$ 满足 $d_p< h_p-1$ ，输出 Drifty，否则输出 hgcnxn。

以这张图为例子说明：

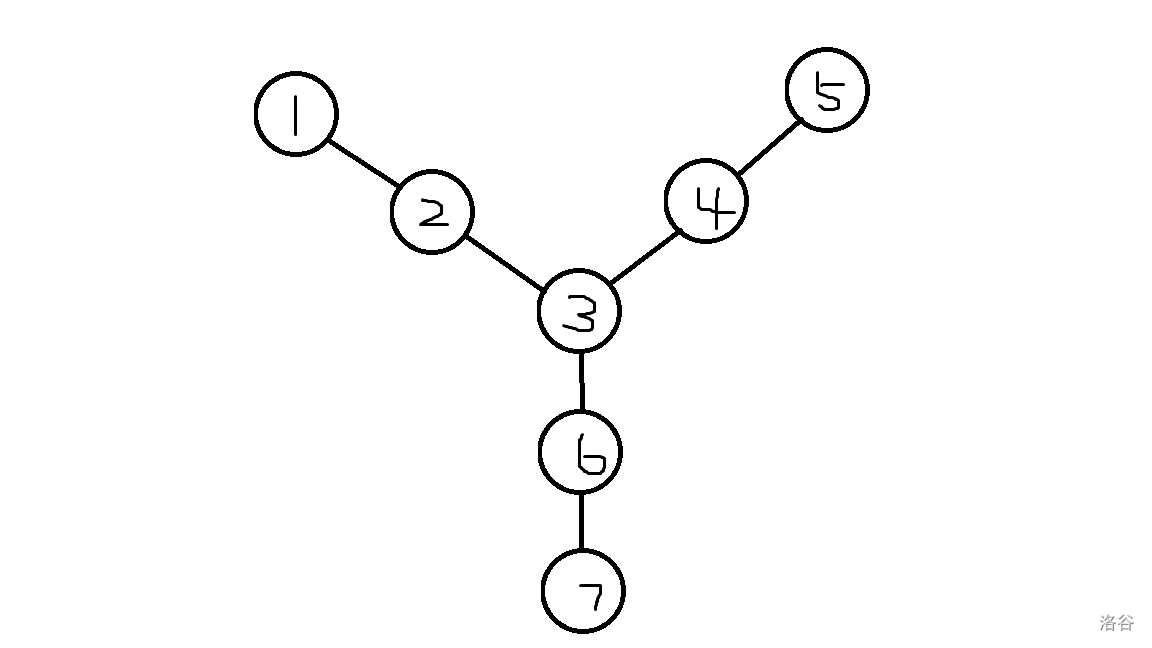
假设 h 在 1 号节点，d 在 3 号节点。此时，对于关键点 3 号节点，$h_3=2$，$d_3=0$。

显然，h 想要捉到 d，他一定要进入 4 号或 6 号节点，由于两者是等价的，不妨设 h 进入了 4 号节点。此时，h 有三种选择：

1. 走进 5 号节点，即选择 1->2->3->4->5 的路线。此时，d 可以选择 3->6->6->6->3 的路线，可以发现，此时 h 在 5 号节点，d 在 3 号节点，两人可以进行无数次这样的行动，即 h 永远也捉不到 d；

2. 回马枪杀回 3 号节点，然后在 2、3、4、6 号节点之间乱逛。显然，d 只要藏在 1、5、7 号节点之中的任意一个即可。

3. 回马枪杀回 3 号节点，然后在 2、3、4、6 号节点之间乱逛一阵之后，回到 1、5、7 号节点之中的任意一个节点，这里假设 h 回到的是 1 号节点。对于这种情况，d 可以选择 3->6->7 的路线，然后在 7 号节点躲无数个回合，直到 h 走 3->2->1 路线的时候，走 7->6->3 的路线，就又回到了开始的状态！

以上是 $d_p< h_p-1$ 的情况。然而，如果不满足这个条件呢？

考虑以下状态：h 在 1 号节点，d 在 6 号节点，此时 $h_3=2$，$d_3=1$。当 h 选择 1->2->3->6->7 的路线时，可以发现，d 必然会被 h 抓住。

综上，得：

对于图中的每一个关键点，若有任何一个关键点 $p$ 满足 $d_p< h_p-1$ ，输出 Drifty，否则输出 hgcnxn。

证明完毕，撒花！（bushi）

下面给出代码：

代码：

#include<bits/stdc++.h>//赛时AC代码，可能有点丑，见谅
using namespace std;
const int maxn=2e5+10;
vector<int>v[maxn];bool b[maxn];//vector存图
queue<int>q;int dist_carry[maxn],dist_be_carried[maxn];
//dist_carry对应h，dist_be_carried对应d;
int n;
void bfs(int s,int a[]){//bfs搜距离
	memset(b,0,sizeof(b));
	memset(a,-1,sizeof(a));
	while(!q.empty())q.pop();
	b[s]=1;q.push(s);a[s]=0;
	while(!q.empty()){
		int x=q.front();q.pop();
		for(int i=0;i<v[x].size();i++){
			int y=v[x][i];
			if(!b[y]){
				b[y]=1;a[y]=a[x]+1;q.push(y);
			}
		}
	}
}
bool istysan(int x){//判断节点x是否为关键点
	if(v[x].size()>2){
		int ans=0;
		for(int i=0;i<v[x].size();i++){
			if(v[v[x][i]].size()>1)ans++;
		}
		if(ans>2)return 1;
	}return 0;
}
bool canrunout(int carry,int be_carried){//判断d能否让h捉不到
	for(int i=1;i<=n;i++){
		if(istysan(i)){
			if(dist_be_carried[i]+1<dist_carry[i])return 1;
		}
	}return 0;
}
int main(){
	ios::sync_with_stdio(0);
	cin.tie(0);cout.tie(0);
	int t;cin>>t;
	while(t--){
		int carry,be_carried;cin>>n>>carry>>be_carried;
		for(int i=1;i<=n;i++)v[i].clear();
		for(int i=1;i<n;i++){
			int p,q;cin>>p>>q;v[p].push_back(q);v[q].push_back(p);
		}bfs(carry,dist_carry);bfs(be_carried,dist_be_carried);
		if(canrunout(carry,be_carried))cout<<"Drifty\n";
		else cout<<"hgcnxn\n";
	}
	return 0;
}

后言： 有什么问题可以在评论区友好讨论