自动搬运

查看原文

来自洛谷，原作者为

	zzlzk **

搬运于2025-08-24 21:20:50，当前版本为作者最后更新于2017-08-22 15:37:24，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

这个题官方正解是高斯消元，可是我不会啊QAQ。

• 说一下搜索怎么做

• 这个题目第一个难点在于你要理解 $n$ 进制的加法

• $n$ 进制的加法就是在十进制的基础上满十进一改成满$n$ 进一

• 由于这道题只考虑加法，所以进位只可能是 $1$ ，证明小学生都会，略

• 搜索的大体思路就是从第 $1$ 位的值开始搜，搜到最后一位，判断是否合法

• 考虑剪枝

• $3$ 个字符串的长度都是 $n$ ，由此可以想到一个最简单的剪枝

• 最高位不能有进位

• 如果有进位，显然第 $3$ 个串的长度不会是 $n$ ，而是$n+1$，这并不合法

• 一个剪枝显然不够啊，再想一个

• 文字不太好描述，我们看图（不会用latex写竖式啊QAQ）

  

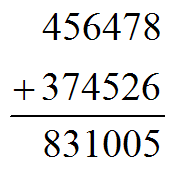
• 假设这是十进制下的加法，怎么判断这个竖式对不对？

• 显然这个竖式是错误的，因为个位上$(8+6) mod 10=4 \not=5$

• 由此推广到每一位，但是还要考虑进位，不慌，看另一张图

  

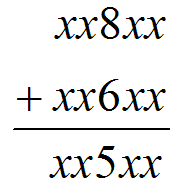
• 这个竖式是对的还是错的？

• 这并不好判断，虽然$(8+6) mod 10=4 \not=5$，但是这是中间位，有可能有进位

• 如果有进位， 那么$(8+6+1) mod 10=5$，这一位就是合法的了。

• 综合上面的分析，得到了另一个剪枝方法

• 用 $A$ 和 $B$ 表示两个加数，用 $C$ 表示两个加数的和

• 如果某 $i$ 位，满足$(A[i]+B[i])mod\;n\not=C[i]$ 和 $(A[i]+B[i]+1)mod\;n\not=C[i]$

• 根据上面的分析，这种状态肯定不对，直接 $return$ 就好了

• 或许还有别的剪枝，但是这两个应该够用了

• 我的代码里还用了一个玄学的 $next$ 数组，有什么用照着样例手推一遍就知道了，比较好理解。实在看不懂可以私信我qwq

学习科学，实用玄学——某钟姓dalao

#include<cstdio>
#include<algorithm>
using namespace std;
#define maxn 30
int a[maxn],b[maxn],c[maxn];
int num[maxn],Next[maxn],n,cnt;
char s1[maxn],s2[maxn],s3[maxn];
bool used[maxn];
bool Judge() {
    for(int i=n-1,x=0;i>=0;i--) {
        int A=num[a[i]],B=num[b[i]],C=num[c[i]];
        if((A+B+x)%n!=C) return false;
        x=(A+B+x)/n;
    }
    return true;
}
bool CanPrune() {//prune: 剪枝—百度翻译。
    if(num[a[0]]+num[b[0]]>=n)
        return true;
    for(int i=n-1;i>=0;i--) {
        int A=num[a[i]],B=num[b[i]],C=num[c[i]];
        if(A==-1||B==-1||C==-1) continue;
        if((A+B)%n!=C&&(A+B+1)%n!=C)
            return true;
    }
    return false;
}
void Print() {
    for(int i=0;i<n;i++)
        printf("%d ",num[i]);
    exit(0);
}
void dfs(int x) {
    if(CanPrune()==true) return;
    if(x==n) {
        if(Judge()==true) Print();
        return;
    }
    for(int i=n-1;i>=0;i--)
        if(used[i]==false) {
            num[Next[x]]=i;
            used[i]=true;
            dfs(x+1);
            num[Next[x]]=-1;
            used[i]=false;
        }
    return;
}
inline int id(char c) {
    return c-'A';
}
void GetNext(int x) {
    if(used[x]==false) {
        used[x]=true;
        Next[cnt++]=x;
    }
    return;
}
int main() {
    scanf("%d",&n);
    scanf("%s%s%s",s1,s2,s3);
    for(int i=0;i<n;i++) {
        a[i]=id(s1[i]);
        b[i]=id(s2[i]);
        c[i]=id(s3[i]);
        num[i]=-1;
    }
    for(int i=n-1;i>=0;i--) {
        GetNext(a[i]);
        GetNext(b[i]);
        GetNext(c[i]);
    }
    for(int i=0;i<n;i++) used[i]=false;
    dfs(0);
    return 0;
}

代码看不懂也可以问我qwq