自动搬运

查看原文

来自洛谷，原作者为

	认真的Ben **

搬运于2025-08-24 21:20:12，当前版本为作者最后更新于2019-08-29 00:05:48，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

---

Debug写了一个下午，写写题解纪念一下，顺便复习刚学的Floyed。本题解是针对初学Floyed的同学写的，请各位大佬忽略。

【算法分析】

这道题目的一种思路是对数字进行宽度优先搜索，但是本蒟蒻尝试写了一下，发现非常麻烦。 具体可参考传送门。

另外还有一些本蒟蒻尚不能理解的高端算法，亦可参考传送门。

题目只要求输出方案总数，那么就要引出我们的算法了，先请出今天的主人公——弗洛伊德（Floyed）算法！

【算法讲解】

看这样一道题目：

给出一张含6个点，9条边的图，要求求出每两个点之间的最短距离。

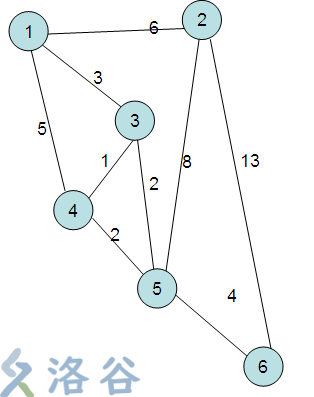
怎么做呢？我刚学的时候考虑的是宽度优先搜索，但这并非正解，为什么呢？

看图，若以宽度优先搜索解此题，我们将观察到栈的变化如下：

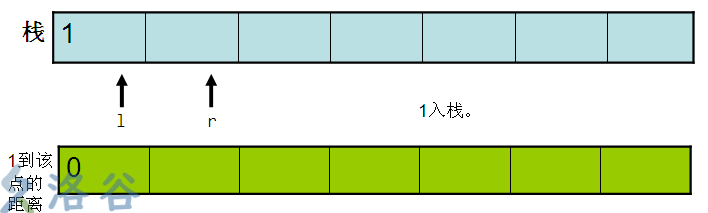
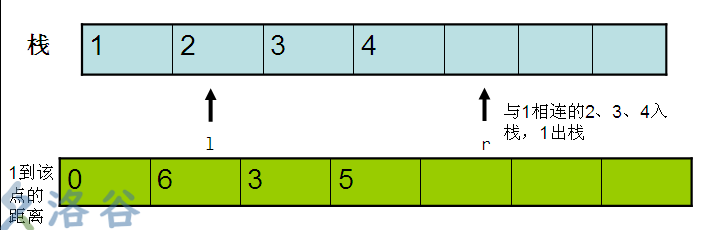
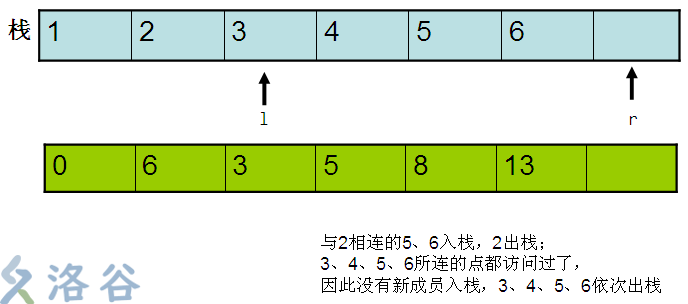
可以看到，宽度优先搜索的想法并不现实，因为宽度优先搜索中，一个点一旦被访问，就不会被二次访问，因此不会更新最优解。要修改宽度优先搜索，就变成了另外一种算法——SPFA了。而且，宽度优先搜索每辆点之间的距离是1，只能计算经过点最少的路径。

回到这里，如何处理这个问题呢？观察1到4的最短路径是1-3-4，可见如果选取中转点，可以使路径变短，这个过程叫做松弛。

以dis[i][j]表示从i到j的最短距离，则有

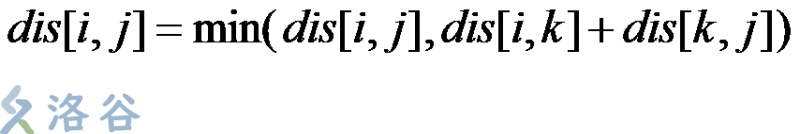
其中1<=i,j,k<=n。

于是我们得到了一个类似区间DP的算法，它的基本框架如下：

memset(dis,0x3f,sizeof(dis));      //初始化为极大值
for(int i=1;i<=n;i++) dis[i][i]=0; //自己到自己不必花费
for(int k=1;k<=n;k++)
{
	for(int i=1;i<=n;i++)
	{
		for(int j=1;j<=n;j++)
		{
			if(dis[i][j]<dis[i][k]+dis[k][j]) dis[i][j]=dis[i][k]+dis[k][j];
		}
	}
}

基本思想是枚举中转点和出发、到达的点，若有更优解就更新更优解。

问题又来了，为什么k要放在外面呢？

原因很简单，DP要保证正确性，就要保证每阶段的决策都是最优解，然而dis[i,k]和dis[k,j]未必在dis[i,j]之前算出，因此会导致一种错误。譬如下图中，从6到7的最短路径本是6-1-5-4-1，但dis[7,5],dis[7,1]和dis[7,4]并未算出，于是遍历了1-7几个中转点后，dis[6,7]还未更新为最优解，就因为i,j在循环外部而不会更新解了。

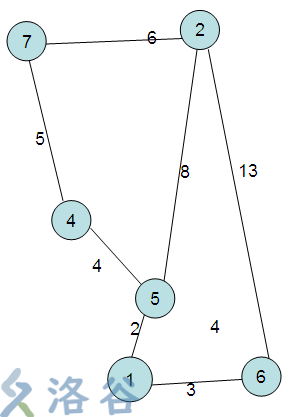
弗洛伊德算法的时间复杂度是O（N^3)，可以处理负边权，也可以求出每两个点之间的最短路。

另外，弗洛伊德算法还可以用于判断两点之间是否有相连的路：

memset(dis,0,sizeof(dis));
for(int k=0;k<=9;k++)
{
	for(int i=0;i<=9;i++)
	{
		for(int j=0;j<=9;j++)
		{
			if(dis[i][j] || (dis[i][k]&&dis[k][j])) dis[i][j]=1;
		}
	}
}

终于讲完啦！

【弗洛伊德算法的运用】

回到本题，观察输入部分：

n k

x_1 y_1

x_2 y_2

... ...

x_k y_k

咦，长得有点像图的输入，仔细分析可以发现：这就是一个有向图呀！

以这样一组数据为例，可以画出这样的图（箭头表示数字的转换关系）：

12040 7

1 2

1 3

4 1

2 5

5 3

4 6

6 0

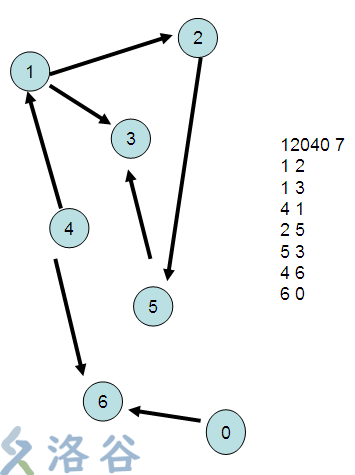
看图可知，

1可以变成2、3,2又可以变成5，共有1（不变）、2、3、5四个可能数字；

同理，2有2、5、3三个可能数字。

3不能变成其他数字，只有一个可能数字。

4可以变成4、1、2、3、5五个可能数字。

5可以变成5、3两个可能数字。

6不能变成其他数字，只有一个可能数字。

0可以变成0、6两个可能数字。

在12040这个数字中，每个数码都可能变为对应的可能数字，根据乘法原理，共有4×3×2×5×2=240种可能数字，并且不会重复。

Q:我们怎么找出每个数字对应的可能数字呢？

A：用弗洛伊德算法啊！

建立一个二维表dis[10][10]，dis[i][j]=1表示数字i可以变成数字j。那么套用刚刚的代码，就可以了！

可是看看这组数据：

222222 2

1 2

2 1

猜猜刚刚的代码会有什么结果？

dis[1]={0,1,1,0,0,0,0,0,0,0};

dis[2]={0,1,1,0,0,0,0,0,0,0};

是的，dis[i][i]=1是不合法的，我们要将它改为0。

for(int i=0;i<=9;i++)
	dis[i][i]=0; //自己不能变回自己 

【代码实现】

Q:怎么知道每个数字可以变成多少个可能数字呢？

A:t[i]表示i能变成多少个可能数字，check[i]=1表示原数字中有这个数码（要不然不能变）。check可以在输入中存储（见输入部分）。如下：

for(int i=0;i<=9;i++)  //枚举初始数据
{
	int tmp=1;         //不变为1种方案
	for(int j=0;j<=9;j++)   //枚举变成的数字
	{
		if(dis[i][j] && check[i]) tmp++; //如果i可以变成j，并且原数字中有这个数码，就多一种方案
	}
	if(s[0]-'0'==i && dis[i][0]) tmp--;   //处理最高位不能变为0的情况 
	if(tmp) t[i]=tmp;  //存储i能变成多少个可能数字
}

Q:n有30位数，最终答案也可能很大，怎么办？

A:高！精！度！

其实这是高精乘低精，因为每个数码对应的可能数字最多也就是10个。

void times(int tmp)  //高精度函数，用于计算答案
{
	int l=strlen(ans),x=0,cnt=0;   //x是每一位的得数，cnt存储进位情况
	if(tmp==10)   //唯一的两位数特别处理
	{
		for(int i=l;i>0;i--) ans[i]=ans[i-1];  //每一位都要前进一位
		ans[0]='0'; //末尾补0
    }
    else
	{
		for(int i=0;i<l;i++)  //注意高精度的数字逆序存储
		{
			x=(ans[i]-'0')*tmp+cnt;  //每一位都与乘数相乘，加上前一位的进位
			cnt=x;     //存一下以免x%10后丢失进位
			if(x>=10)
			{
				x%=10;	//只保留个位
			}
			ans[i]=x+'0';
			cnt=(cnt-x)/10;   //剩下的交给下一位
		}
		if(cnt) ans[l]=cnt+'0';  //如果乘第一位后还有进位，再填前一位
	}
}

Q:输入输出怎么办？

A:以字符串输入，以字符串输出。

scanf("%s %d",s,&K);  
int L=strlen(s);
for(int i=0;i<L;i++) 
	check[s[i]-'0']++;   //记录每一个数码有无出现
ans[0]='1';              //初值要赋为1而不是0
memset(dis,0,sizeof(dis));  //弗洛伊德算法要初始化，养成好习惯

for(int i=1;i<=K;i++)
{
	int a,b;
	cin>>a>>b;
	dis[a][b]=1;       //注意这里存的是有向图
} 

for(int i=0;i<L;i++) 
    if(t[s[i]-'0'])    //0不能乘上去
        times(t[s[i]-'0']);  //乘上数码所对应的可能数字数目
	
int L_=strlen(ans);
for(int i=L_-1;i>=0;i--) cout<<ans[i];  //逆序输出

经历这么多以后，我们终于迎来了最爱的

【AC代码】

#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
char ans[40],s[40];int K,check[10],dis[10][10],t[10];

void times(int tmp)
{
	int l=strlen(ans),x=0,cnt=0;
	if(tmp==10)
	{
		for(int i=l;i>0;i--) ans[i]=ans[i-1];
		ans[0]='0';
    }
    else
	{
		for(int i=0;i<l;i++)
		{
			x=(ans[i]-'0')*tmp+cnt;
			cnt=x;
			if(x>=10)
			{
				x%=10;	
			}
			ans[i]=x+'0';
			cnt=(cnt-x)/10;
		}
		if(cnt) ans[l]=cnt+'0';
	}
}
int main()
{
	scanf("%s %d",s,&K);
	int L=strlen(s);
	for(int i=0;i<L;i++) 
	    check[s[i]-'0']++;
	ans[0]='1';
	memset(dis,0,sizeof(dis));
	
	for(int i=1;i<=K;i++)
	{
		int a,b;
		cin>>a>>b;
		dis[a][b]=1;
	} 
	
	for(int k=0;k<=9;k++)
	{
		for(int i=0;i<=9;i++)
		{
			for(int j=0;j<=9;j++)
			{
				if(dis[i][j] || (dis[i][k]&&dis[k][j])) dis[i][j]=1;
			}
		}
	}
	for(int i=0;i<=9;i++)
		dis[i][i]=0; //自己不能变回自己 
	for(int i=0;i<=9;i++) 
	{
		int tmp=1;
		for(int j=0;j<=9;j++)
		{
			if(dis[i][j] && check[i]) tmp++;
		}
		if(s[0]-'0'==i && dis[i][0]) tmp--;//处理最高位不能变为0的情况 
		t[i]=tmp;
	}
	for(int i=0;i<L;i++) if(t[s[i]-'0']) times(t[s[i]-'0']);
	
	int L_=strlen(ans);
	for(int i=L_-1;i>=0;i--) cout<<ans[i];
	return 0;
}

上面的程序片段已经有详细注释了，我犯懒就不贴了。

【总结】

1、弗洛伊德算法的时间复杂度是O（N^3)，数据范围小于500时适用。可以处理负边权。可以求出每两个点之间的最短路，适用于多次提问的题目。弗洛伊德算法还可以用于判断两点之间是否有通路。不要忘了k要放在最外层，不要忘了初始化。

2、图论题目可能会变出许多形式，但是我们要善于在图的立场上思考，怎样把题目变成图？有什么算法可以解决？

3、熟悉高精度的写法。

PS：码字不易，希望支持！