自动搬运

查看原文

来自洛谷，原作者为

	AFewSuns 弱省弱校蒟蒻，tcl，zbl

搬运于2025-08-24 22:55:58，当前版本为作者最后更新于2024-03-13 11:51:04，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

题目大意

给定一张三角剖分图，外圈按顺序标号为 $1\sim n$。定义一次操作为删除一条边，再加入一条边得到一个新的三角剖分。

有 $q$ 次修改或询问，每次会进行一次合法操作，或询问一个点 $x$，求最少进行多少次操作使得所有对角线都有共同端点 $x$，以及达到最少操作次数的方案数。

$4 \leq n \leq 2\times 10^5,1 \leq q \leq 2\times 10^5$。

题目分析

首先操作数的下界就是顶点不含 $x$ 的对角线个数，而事实上这个下界很容易取到，所以只需要考虑方案数。

按照这个下界手玩一下，便可以发现新增边的加入顺序会有一定的先后关系，即加入某条边之前必须先加入另一条边：

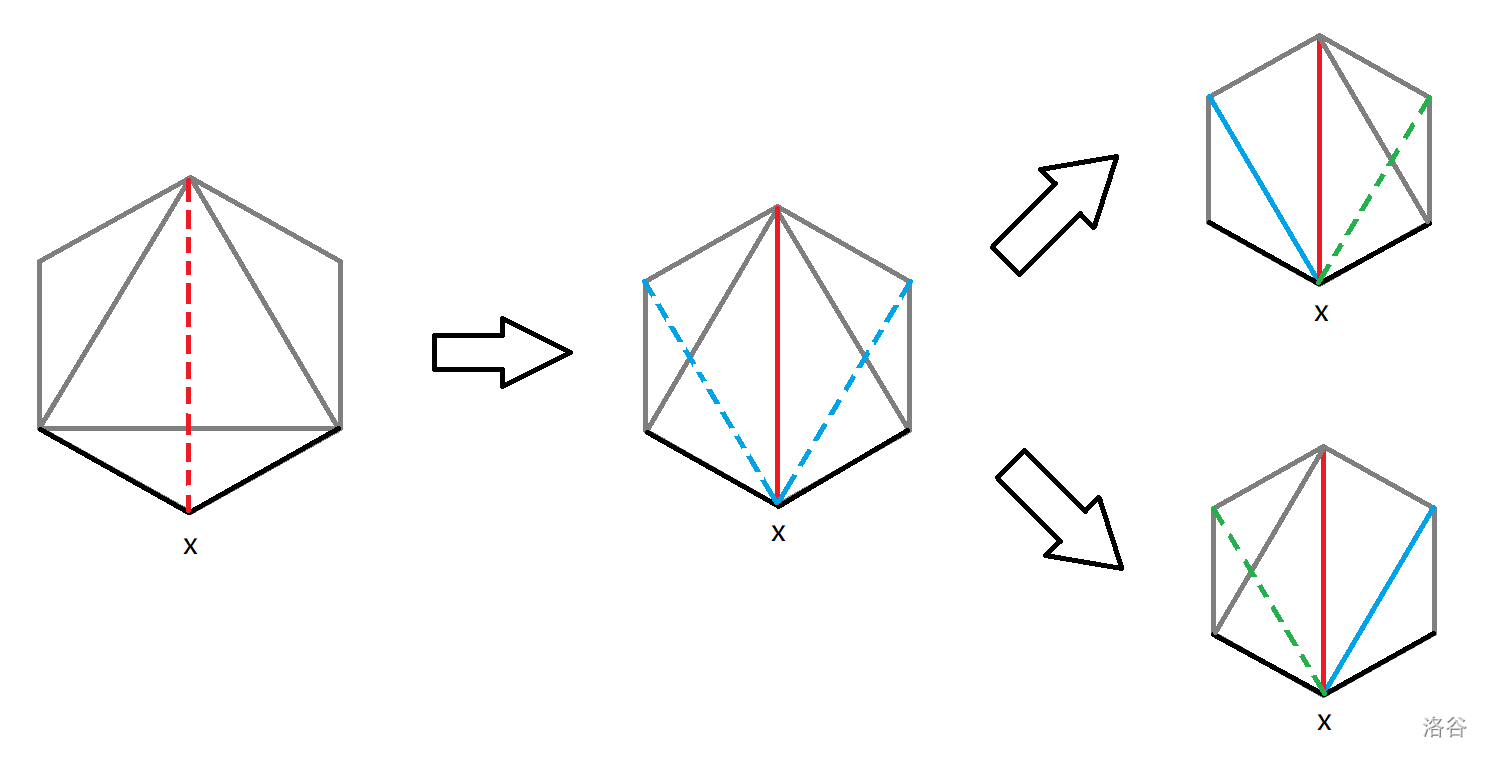
如图，只有在加入红色边之后才能加入另外两条边，故方案数为 $2$。

以此类推，可以发现其先后顺序会形成一种树形结构，必须按照树的拓扑序进行加边：

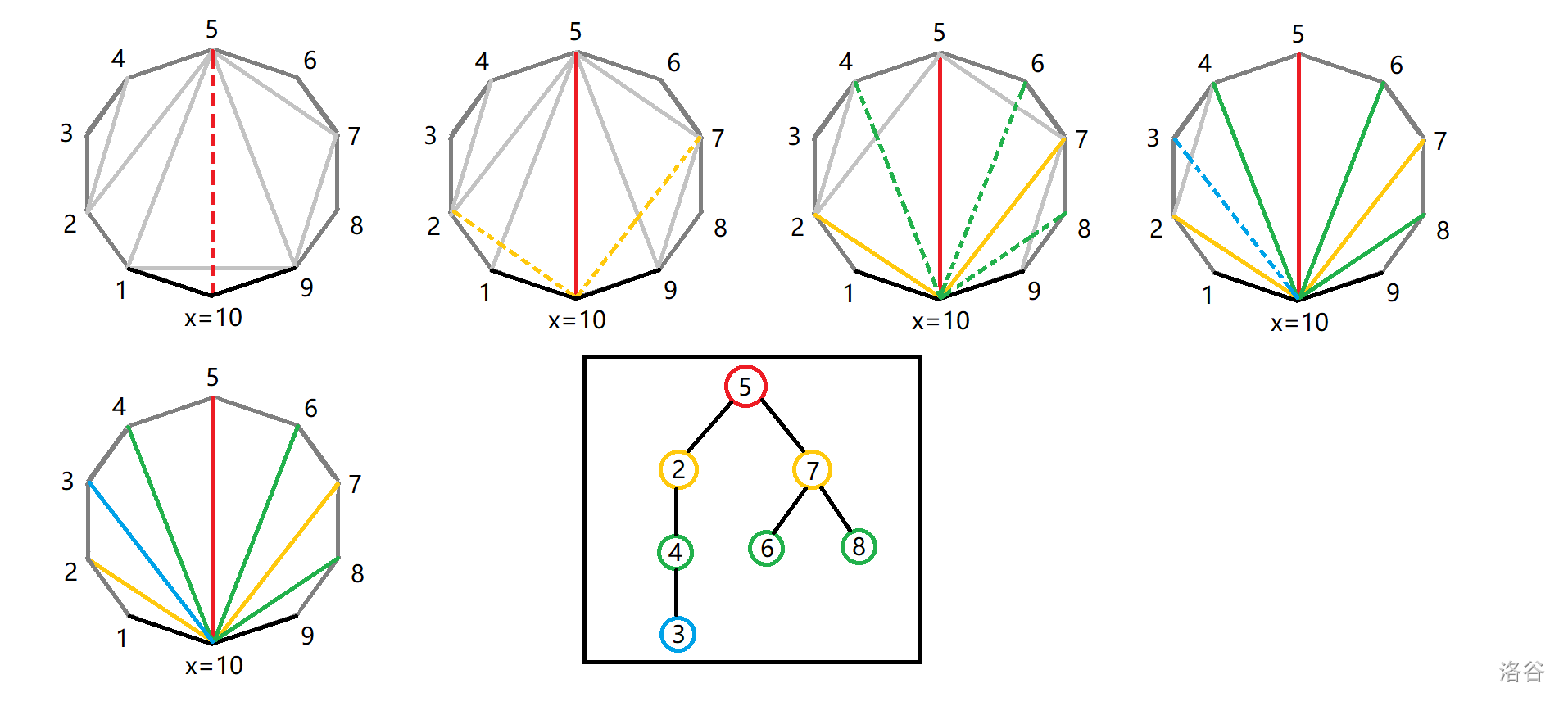
其中不交的两棵子树之间互相独立（中间的边会将两边分开），于是方案数即为这棵树的拓扑序个数。

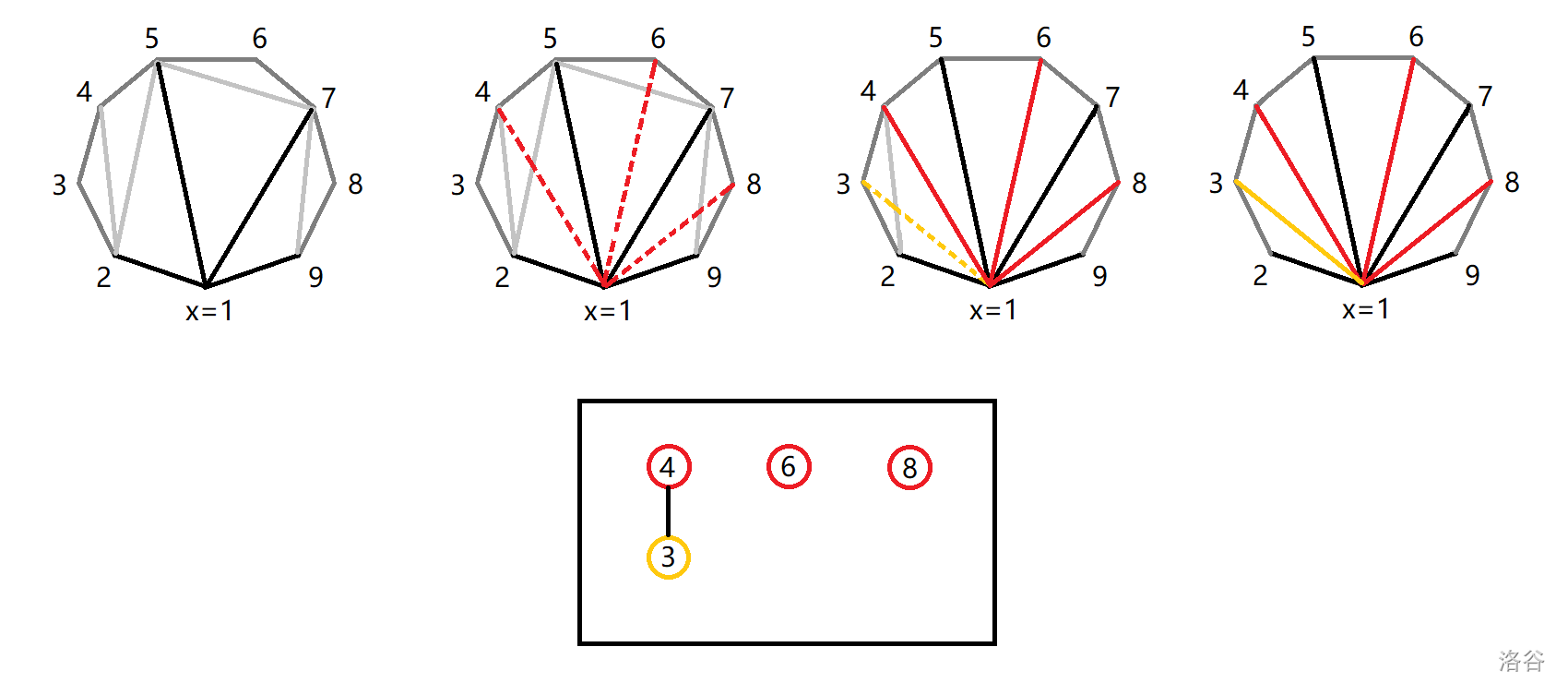
上图为样例二的示意图。可以发现，当初始有对角线顶点包含 $x$ 的时候，这些对角线划分出来的区域互相独立，最终也会形成若干棵树。

而树的拓扑序方案数即为 $\dfrac{n!}{\prod\limits_{i=1}^{n}{siz_i}}$，其中 $siz_i$ 为 $i$ 子树的大小，$n$ 为总节点个数，在题目中的显现即为第一问（最少操作次数）的答案。

考虑如何在原图中快速刻画这棵树。将三角剖分形成的树画出来：

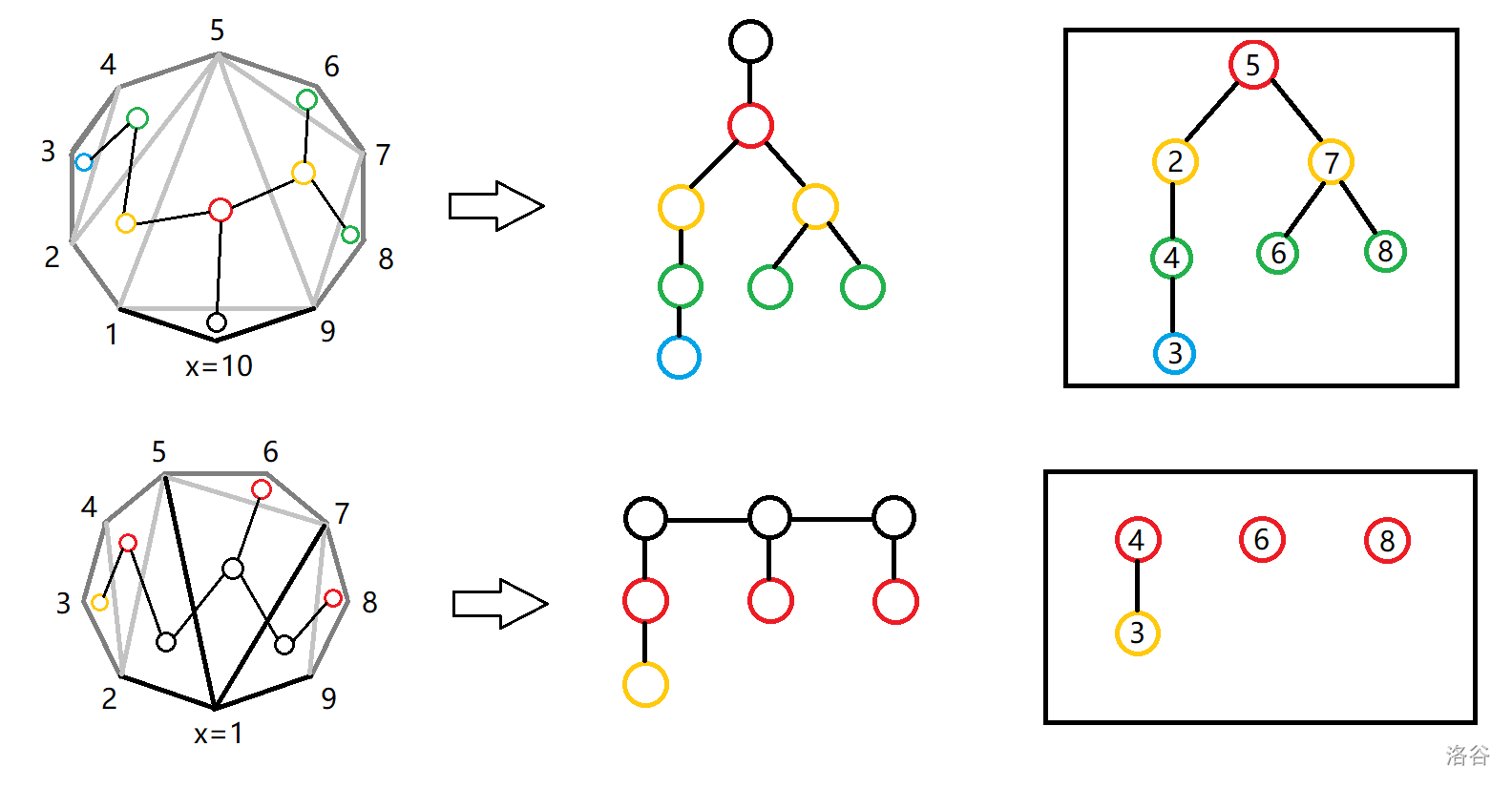
对比发现除去黑点之后，这就是我们想要的树，而黑点就是相邻两个顶点包含 $x$ 的边中间夹成的三角形。证明比较容易，在此省略。

于是现在的主要问题在于如何维护 $\prod\limits_{i}{siz_i}$，修改就相当于删边加边。考虑树上的一个点（非黑点）及其子树，它在原图上其实代表着一段完整圆弧，设其为 $[l,r]$，那么这个子树的大小即为中间剖出来的三角形个数，为 $r-l-1$。而它是非黑点的条件也很简单，即 $[l,r]$ 不能包括 $x$。

现在这道题的做法已经呼之欲出了：对于每条对角线 $(x,y)$，将没被 $x\to y$ 这段圆弧包含的点除以 $len_{x\to y}-1$；将没被 $y\to x$ 这段圆弧包含的点除以 $len_{y\to x}-1$。这是一个区间乘，单点查询问题，使用树状数组即可做到 $\mathcal O((n+q)\log n)$。

代码

#include<bits/stdc++.h>
using namespace std;
using namespace my_std;
#define mod 1000000007
ll n,q,jc[200020],jcinv[200020],invv[200020],sum[200020],tree[200020];
il ll lowbit(ll x){
	return x&(-x);
}
il void mdf(ll x,ll v){
	if(v<0) v=-v;
	else v=invv[v];
	while(x<=n){
		tree[x]=tree[x]*v%mod;
		x+=lowbit(x);
	}
}
il ll query(ll x){
	ll res=1;
	while(x){
		res=res*tree[x]%mod;
		x-=lowbit(x);
	}
	return res;
}
il void solve(ll x,ll y,ll t){
	sum[x]-=t;
	ll len=(y-x+n)%n-1;
	swap(x,y);
	x=x%n+1;
	y=(y+n-2)%n+1;
	if(x<=y){
		mdf(x,t*len);
		mdf(y+1,-t*len);
	}
	else{
		mdf(x,t*len);
		mdf(1,t*len);
		mdf(y+1,-t*len);
	}
}
int main(){
	n=read();
	q=read();
	jc[0]=1;
	fr(i,1,n) jc[i]=jc[i-1]*i%mod;
	jcinv[n]=inv(jc[n],mod);
	pfr(i,n-1,0) jcinv[i]=jcinv[i+1]*(i+1)%mod;
	fr(i,1,n) invv[i]=jcinv[i]*jc[i-1]%mod;
	fr(i,1,n) sum[i]=n-3;
	fr(i,1,n) tree[i]=1;
	fr(i,1,n-3){
		ll x=read(),y=read();
		solve(x,y,1);
		solve(y,x,1);
	}
	while(q--){
		ll opt=read();
		if(opt==1){
			ll x=read(),y=read(),xx=read(),yy=read();
			solve(x,y,-1);
			solve(y,x,-1);
			solve(xx,yy,1);
			solve(yy,xx,1);
		}
		else{
			ll x=read();
			pf("%lld %lld\n",sum[x],jc[sum[x]]*query(x)%mod);
		}
	}
}