自动搬运

查看原文

来自洛谷，原作者为

	云浅知处 喵

搬运于2025-08-24 22:52:56，当前版本为作者最后更新于2023-12-22 20:16:09，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

考虑建一个 DFS 树，那么非树边都是返祖边。

考虑 $(u,v)$ 这样一条非树边，这里 $u$ 是 $v$ 的祖先。在删掉 $u$ 和 $v$ 之后图长这样：

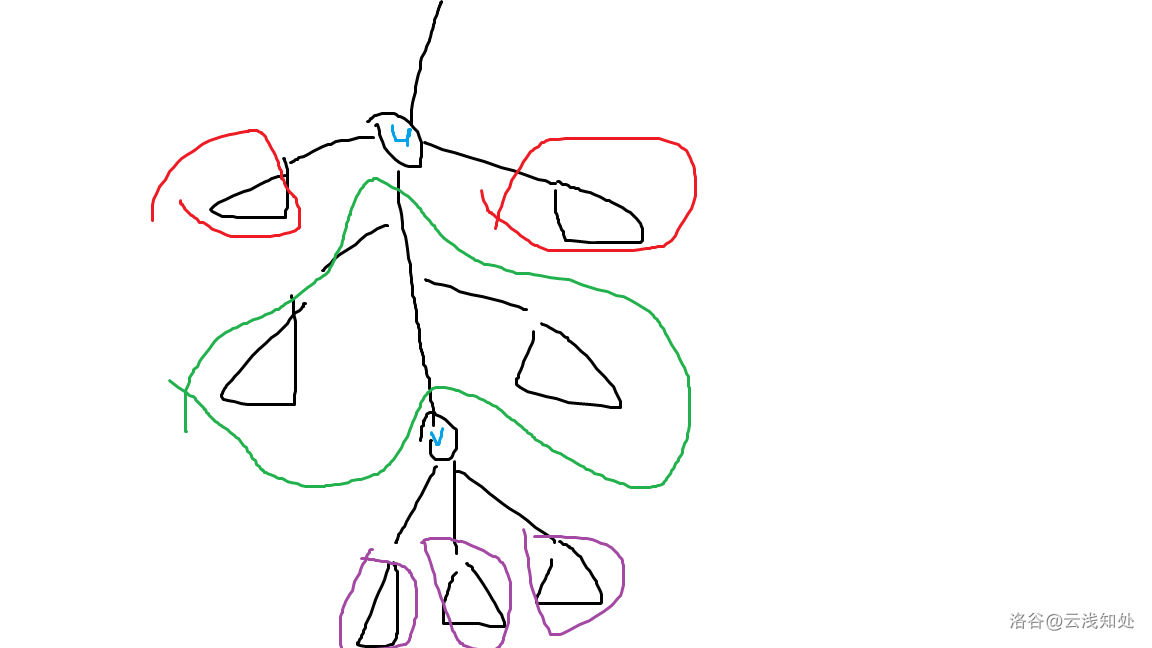
这里紫色部分和红色部分都可能不存在，但由于我们限定这是一条非树边因此绿色部分一定存在。$u$ 上面的部分也可能不存在，但稍后我们会看到这并不影响判断，

首先红色部分必须存在向上的连边否则就会和绿色部分分开。因此我们可以把红色部分和 $u$ 上面的部分看作一个整体。当 $u$ 为根节点的时候红色部分不存在，不过这不会影响我们的判断。

注意到绿色部分也是一个整体的连通块，紫色部分会构成若干连通块。那么紫色部分的每个子树要么和绿色部分有连边，要么和红色部分有连边（且红色部分存在）。我们分几类情况讨论：

• 存在一个紫色的子树和红绿均无连边：这个子树会被分割为独立的一个连通块，一定不合法。
• 存在一个紫色的子树同时和红绿均有连边（且红色部分存在）：（在判掉上面那种情况的前提下）一定合法。
• 每个紫色的子树都只和红色或绿色中的一个连边：这时需要绿色部分和红色部分有连边，或者红色部分不存在。

考虑三种情况怎么判，发现只需要维护某个子树内最浅和最深的一条返祖边，可以用线段树合并或启发式合并求出。对于第三种情况，绿色部分可以写成 DFS 序上的 $O(1)$ 个连续段，维护 DFS 序区间最小值即可。对于求出绿色部分顶端的点，发现本质上是树上 $k$ 级祖先。

接下来我们考虑树边怎么判。设 $u=fa_v$，有以下情况：

• $u$ 是根节点：如果 $u$ 在 DFS 树上的儿子数量 $\ge 3$ 一定无解，如果 $u$ 在 DFS 树上的儿子数量 $=2$ 那么要求 $v$ 在删去 $u$ 之后是一个孤立点。如果 $u$ 在 DFS 树上的儿子只有 $v$，那么这要求 $v$ 在 DFS 树上也只有一个儿子，或者 $v$ 是孤立点。
• $u$ 不是根节点：要求 $u$ 的除了 $v$ 的每个儿子都得有向上的连边，然后如果 $v$ 有儿子就必须连到 $u$ 的祖先上。

时间复杂度：$O(m\log n)$ 或 $O(m\log^2n)$。

//-DYUNQIAN -std=c++14 -O2 -Wall
#include<bits/stdc++.h>

#define ll long long
#define fi first
#define se second
#define mk make_pair

using namespace std;

inline int read(){
    int x=0,f=1;char c=getchar();
    for(;(c<'0'||c>'9');c=getchar()){if(c=='-')f=-1;}
    for(;(c>='0'&&c<='9');c=getchar())x=x*10+(c&15);
    return x*f;
}

void cmax(int &x,int v){x=max(x,v);}
void cmin(int &x,int v){x=min(x,v);}

const int N=3e5+5;
vector<int>G[N],adj[N];
vector<int>R[N];
set<int>S[N];
int n,m;

struct SegTree{
	int M,k,d[N<<2];
	void upd(int p){d[p]=min(d[p<<1],d[p<<1|1]);}
	void build(int n,vector<int>A){
		k=0,M=1;while(M<n)M<<=1,k++;
		for(int i=1;i<=M+M;i++)d[i]=n+1;
		for(int i=1;i<=n;i++)d[i+M-1]=A[i];
		for(int i=M-1;i>=1;i--)upd(i);
	}
	int qmin(int l,int r){
		int res=n+1;
		for(l+=M-1,r+=M;l<r;l>>=1,r>>=1){
			if(l&1)cmin(res,d[l++]);
			if(r&1)cmin(res,d[--r]);
		}
		return res;
	}
}T;

int dep[N],fa[N],sz[N],dfn[N],top[N],hson[N],dfc,pos[N],id[N];
void dfs1(int u,int de){
	dep[u]=de,sz[u]=1;
	for(int v:G[u]){
		if(v==fa[u])continue;
		fa[v]=u,dfs1(v,de+1),sz[u]+=sz[v];
		if(sz[v]>sz[hson[u]])hson[u]=v;
	}
}
void dfs2(int u,int tp){
	top[u]=tp,dfn[u]=++dfc,id[dfc]=u;
	if(hson[u])dfs2(hson[u],tp);
	for(int v:G[u]){
		if(v==fa[u]||v==hson[u])continue;
		dfs2(v,v);
	}
}
int getnode(int u,int v){
	assert(dfn[v]>=dfn[u]&&dfn[v]<=dfn[u]+sz[u]-1);
	int de=dep[u]+1;
	while(dep[top[v]]>de)v=fa[top[v]];
	int dis=dep[v]-de;
	return id[dfn[v]-dis];
}

struct BIT{
	int c[N];
	void clear(){memset(c,0,sizeof(c));}
	int lowbit(int x){return x&(-x);}
	void Add(int x,int v){for(int i=x;i<=n;i+=lowbit(i))c[i]+=v;}
	int sum(int x){int res=0;for(int i=x;i;i-=lowbit(i))res+=c[i];return res;}
	void add(int l,int r,int v){if(l<=r)Add(r+1,-v),Add(l,v);}
	int qval(int x){return sum(x);}
}W;

signed main(void){

#ifdef YUNQIAN
    freopen("in.in","r",stdin);
//    freopen("out.out","w",stdout);
#endif
	
	n=read(),m=read();
	vector<pair<int,int> >E;vector<int>deg(n+1,0);
	for(int i=1;i<=m;i++){
		int u=read(),v=read();E.emplace_back(mk(u,v));
		adj[u].emplace_back(v),adj[v].emplace_back(u),deg[u]++,deg[v]++;
	}
	
	vector<bool>vis(n+1,0);
	function<void(int,int)>buildtree=[&](int u,int fa){
		vis[u]=1;
		for(int v:adj[u]){
			if(!vis[v])dep[v]=dep[u]+1,buildtree(v,u),G[u].emplace_back(v);
			else if(dep[v]<dep[u]&&v!=fa)R[u].emplace_back(v);
		}
	};
	dep[1]=1,buildtree(1,0);
	dfs1(1,1),dfs2(1,1);
	
	vector<int>val(n+1,n+1);
	for(int i=1;i<=n;i++){
		for(int j:R[i])cmin(val[dfn[i]],dep[j]);
	}
	T.build(n,val);
	
	auto Merge=[&](set<int>&A,set<int>&B){
		if(A.size()<B.size())swap(A,B);
		for(int x:B)A.insert(x);B.clear();
	};
	
	vector<int>mxlow(n+1,0),mnlow(n+1,0);// max/min low
	function<void(int)>getlow=[&](int u){
		for(int v:G[u])getlow(v),Merge(S[u],S[v]);
		for(int j:R[u])S[u].insert(dep[j]);
		S[u].erase(S[u].lower_bound(dep[u]-1),S[u].end());
		if(S[u].size())mxlow[u]=*--S[u].end(),mnlow[u]=*S[u].begin();
		else mxlow[u]=0,mnlow[u]=n+1;
	};
	getlow(1);
	
	W.clear();vector<int>cut(n+1,0);
	
	fill(vis.begin(),vis.end(),0);
	map<pair<int,int>,bool>Ans;
	
	auto addres=[&](int u,int v){Ans[mk(u,v)]=Ans[mk(v,u)]=1;};
	auto getans=[&](int u){
		// (u,son[u]) | (anc[u],u)
		if(u==1){
			if(G[u].size()>=3)return ;
			if(G[u].size()==2){
				for(int v:G[u])if(sz[v]==1)addres(u,v);
			}
			if(G[u].size()==1){
				int v=G[u][0];
				if(G[v].size()<=1)addres(u,v);
			}
			return ;
		}
		for(int v:G[u]){
			if(mnlow[v]==mxlow[v])vis[mnlow[v]]=1;
			W.add(mnlow[v]+1,mxlow[v]-1,1);
		}
		for(int v:G[u]){
			if(mnlow[v]>=dep[u])cut[u]--;
			if(cut[u]==0){
				bool chk=1;
				for(int j:G[v])if(mnlow[j]>=dep[u])chk=0;
				if(chk)addres(u,v);
			}
			if(mnlow[v]>=dep[u])cut[u]++;
		}
		
		if(cut[u]>=1)goto ED2;
		for(int j:R[u]){
			int x=getnode(j,u);
			if(mnlow[x]>=dep[j])cut[j]--;
			if(cut[j]==0){
				if(vis[dep[j]])goto ED;
				if(W.qval(dep[j])>=1){addres(u,j);goto ED;}
				if(j==1){addres(u,j);goto ED;}
				if(T.qmin(dfn[x],dfn[u]-1)<dep[j]||T.qmin(dfn[u]+sz[u],dfn[x]+sz[x]-1)<dep[j])addres(u,j);
			}
			ED:if(mnlow[x]>=dep[j])cut[j]++;
		}
		
		ED2:for(int v:G[u]){
			if(mnlow[v]==mxlow[v])vis[mnlow[v]]=0;
			W.add(mnlow[v]+1,mxlow[v]-1,-1);
		}
	};
	
	for(int i=1;i<=n;i++)for(int j:G[i])cut[i]+=(mnlow[j]>=dep[i]);
	for(int i=1;i<=n;i++)getans(i);
	int res=0;for(auto e:E)res+=(Ans[mk(e.fi,e.se)]==0);cout<<res<<endl;

    return 0;
}