1 条题解
-
0
自动搬运
来自洛谷,原作者为

liangbowen
不能再摆了,,,搬运于
2025-08-24 22:52:35,当前版本为作者最后更新于2023-11-23 17:20:46,作者可能在搬运后再次修改,您可在原文处查看最新版自动搬运只会搬运当前题目点赞数最高的题解,您可前往洛谷题解查看更多
以下是正文
blog。NOIP2023 T3,特殊性质题。
什么是特殊性质题?就是题目给出了你极其神秘的性质,从而引导你想出正解。
本篇题解将从部分分的角度,一步步讲述部分分与正解的关系。这样看的话,本题会变得十分简单。
,
首先转换题意。,本质上就是满足两者中的一个:
- 所有 都有 。
- 所有 都有 。
这两件事情本质相同,我们只考虑第一件事情(),第二件事情就是将 对调一下再处理。
你想一想拓展的本质。其实就是有两个指针 与 ,每次如果有 ,那么可以做:
- ,表示 的下一位是 , 的下一位仍然是 。
- ,表示 的下一位仍然是 , 的下一位是 。
- ,表示 的下一位是 , 的下一位是 。
于是考虑 DP。 表示 匹配到第 位, 匹配到第 位,是否可行。转移即:
$$X_i<Y_j, dp_{i,j}\gets dp_{i-1,j}\cup dp_{i,j-1}\cup dp_{i-1,j-1} $$答案即 。这一部分的代码如下,时间复杂度 。
#include <iostream> #include <cstdio> #include <cassert> using namespace std; const int N = 5e5 + 5; bool dp[2005][2005]; bool chk(int x[], int y[], int n, int m) //是否可以构造出 fi<gi { if (x[1] <= y[1] || x[n] <= y[m]) return false; //特判 for (int i = 1; i <= n; i++) for (int j = 1; j <= m; j++) dp[i][j] = false; //初始化 dp[1][1] = true; //(1,1) 作为起点,显然可以到达 for (int i = 1; i <= n; i++) for (int j = 1; j <= m; j++) //下面的转移方程就和思路中的一样 if (x[i] > y[j]) dp[i][j] |= (dp[i - 1][j - 1] | dp[i - 1][j] | dp[i][j - 1]); return dp[n][m]; } int x[N], y[N], ttx[N], tty[N]; int main() { int n, m, q; scanf("%*d%d%d%d", &n, &m, &q); for (int i = 1; i <= n; i++) scanf("%d", &x[i]); for (int i = 1; i <= m; i++) scanf("%d", &y[i]); putchar(chk(x, y, n, m) || chk(y, x, m, n) ? '1' : '0'); while (q--) { for (int i = 1; i <= n; i++) ttx[i] = x[i]; for (int i = 1; i <= m; i++) tty[i] = y[i]; int cx, cy; scanf("%d%d", &cx, &cy); while (cx--) {int p, v; scanf("%d%d", &p, &v); ttx[p] = v;} while (cy--) {int p, v; scanf("%d%d", &p, &v); tty[p] = v;} putchar(chk(ttx, tty, n, m) || chk(tty, ttx, m, n) ? '1' : '0'); } return 0; }, 特殊性质
考虑上面那个做法是在干啥。
令 ,从 开始,每次可以向右、下、右下的 的点走一步,问能否走到 。
首先,如果 ,说明 的那一列的全部 都是 。显然路被堵死了,走不到捏。
同理, 也是走不到。
考虑完这些小情况后,根据这个特殊性质,必然有:
- 对于 ,都有 。
- 对于 ,都有 。
这说明,只要我们能走到第 行或者第 列,就一定能顺着这条通路到达 。看起来像下面这样:
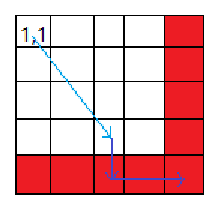
以此类推,找到 的最小值,如果有 ,说明:对于 ,都有 。
这说明,只要我们能走到第 行或者第 列,就一定能顺着这条通路到达第 行或者第 列,然后再到达 。
同样地,列也可以类似地操作。
可以理解为,现在有一个边框,你只要到达了边框就能走到 了。那么每次缩小整个边框地大小,必然是不会更劣的。
于是你一直缩小边框,如果中途无法缩小( 且 ),不可行;否则,如果边框到达了 ,那么就是可行。
实现方面可以采用递归,维护前缀最小值 / 最大值的位置即可。时间复杂度 。
bool check(int x, int y) //能否从 (1,1) 走到第 x 行或者第 y 列 { if (x == 1 || y == 1) return true; //如果刚好是第 1 行或者第 1 列,可行 Node X = preX[x - 1], Y = preY[y - 1]; //找到前缀最值的位置 if (f[X.min] < g[Y.min]) return check(X.min, y); if (g[Y.max] > f[X.max]) return check(x, Y.max); return false; }正解
特殊性质的提示性非常强。你可以找到 的最小值与 的最大值的位置。
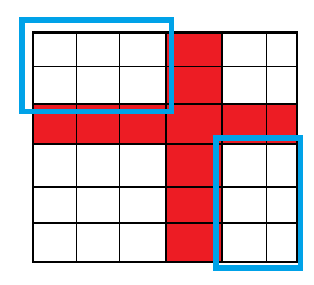
如图所示,分左上与右下两个区域,如果 能走到红线部分,并且红线部分能走到 ,那么就是可行了。
所以,你只要实现两个
check()函数,一个看左上部分的合法性,一个看右下部分的合法性即可。完整代码如下,时间复杂度 。
#include <iostream> #include <cstdio> #include <cassert> using namespace std; const int N = 5e5 + 5; int f[N], g[N]; struct Node {int min, max; Node(int ge = 0, int fe = 0): min(ge), max(fe){}} preX[N], preY[N], sufX[N], sufY[N]; #define update(T, p) (Node){T[i] < T[p.min] ? i : p.min, T[i] > T[p.max] ? i : p.max}; bool check1(int x, int y, int n, int m) //左上区域 { if (x == 1 || y == 1) return true; Node X = preX[x - 1], Y = preY[y - 1]; if (f[X.min] < g[Y.min]) return check1(X.min, y, n, m); if (g[Y.max] > f[X.max]) return check1(x, Y.max, n, m); return false; } bool check2(int x, int y, int n, int m) //右下区域,同左上区域 { if (x == n || y == m) return true; Node X = sufX[x + 1], Y = sufY[y + 1]; if (f[X.min] < g[Y.min]) return check2(X.min, y, n, m); if (g[Y.max] > f[X.max]) return check2(x, Y.max, n, m); return false; } bool solve(int tmpf[], int tmpg[], int n, int m) { if (tmpf[1] >= tmpg[1]) return false; //一个特判 for (int i = 1; i <= n; i++) f[i] = tmpf[i]; //copy 一下,方便在全局定义函数 for (int i = 1; i <= m; i++) g[i] = tmpg[i]; //这里求出 X,Y 的前后缀 最大/最小值 的位置,为了让代码更优美,使用了 update() for (int i = 1; i <= n; i++) preX[i] = (i == 1) ? (Node){1, 1} : update(f, preX[i - 1]); for (int i = 1; i <= m; i++) preY[i] = (i == 1) ? (Node){1, 1} : update(g, preY[i - 1]); for (int i = n; i >= 1; i--) sufX[i] = (i == n) ? (Node){n, n} : update(f, sufX[i + 1]); for (int i = m; i >= 1; i--) sufY[i] = (i == m) ? (Node){m, m} : update(g, sufY[i + 1]); Node X = preX[n], Y = preY[m]; //找出两条红线的位置 if (f[X.min] >= g[Y.min] || g[Y.max] <= f[X.max]) return false; //一个特判 return check1(X.min, Y.max, n, m) && check2(X.min, Y.max, n, m); //分左上右下递归即可 } int tx[N], ty[N], ttx[N], tty[N]; int main() { int n, m, q; scanf("%*d%d%d%d", &n, &m, &q); for (int i = 1; i <= n; i++) scanf("%d", &tx[i]); for (int i = 1; i <= m; i++) scanf("%d", &ty[i]); putchar(solve(tx, ty, n, m) || solve(ty, tx, m, n) ? '1' : '0'); while (q--) { for (int i = 1; i <= n; i++) ttx[i] = tx[i]; for (int i = 1; i <= m; i++) tty[i] = ty[i]; int cx, cy; scanf("%d%d", &cx, &cy); while (cx--) {int p, v; scanf("%d%d", &p, &v); ttx[p] = v;} while (cy--) {int p, v; scanf("%d%d", &p, &v); tty[p] = v;} putchar(solve(ttx, tty, n, m) || solve(tty, ttx, m, n) ? '1' : '0'); } return 0; }希望能帮助到大家 /qq。
- 1
信息
- ID
- 9427
- 时间
- 1000ms
- 内存
- 512MiB
- 难度
- 6
- 标签
- 递交数
- 0
- 已通过
- 0
- 上传者
