自动搬运

查看原文

来自洛谷，原作者为

	Diaоsi Enemy of God

搬运于2025-08-24 22:52:22，当前版本为作者最后更新于2024-05-23 17:52:20，作者可能在搬运后再次修改，您可在原文处查看最新版

自动搬运只会搬运当前题目点赞数最高的题解，您可前往洛谷题解查看更多

以下是正文

[ICPC2021 Nanjing R] Paimon Polygon

恶心题，先分类讨论。

由于 $O$ 这个点比较特殊，我们可以从它入手，讨论它是否在 $\mathbb{S}\cup \{O\}$ 的凸包上。下文中的凸包都默认为严格凸包，即凸包轮廓上不存在三点共线。

第一种情况：$O\in C_{\mathbb{S}\cup \{O\}}$

对于这种情况，答案可能有两类，一类是完全包含，另一类是以极角序相邻的点作为分界。需要进一步划分。

1. 完全包含： 此时外层的凸包只能是 $C_{\mathbb{S}\cup \{O\}}$，把这个凸包求出来之后判断剩余的点和 $O$ 是否构成一个凸包即可。

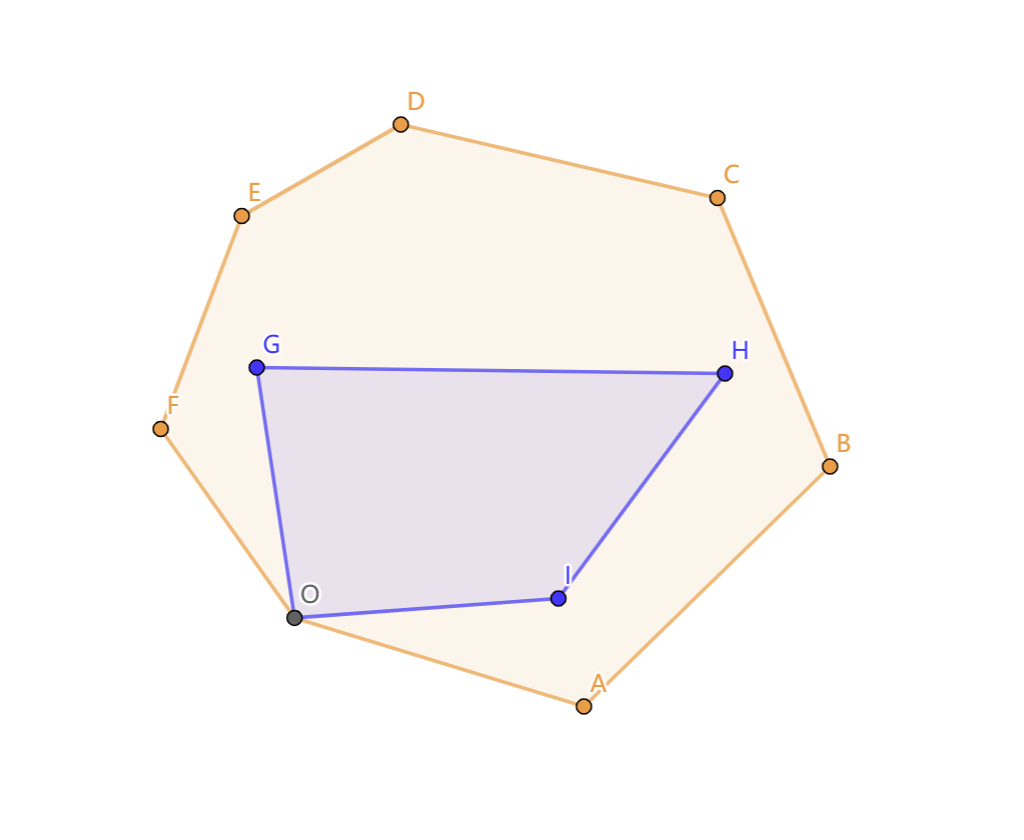
但是此时内层的凸包不一定合法，题目中要求两个凸包的交只能是 $O$，所以还要判掉下面这种情况：

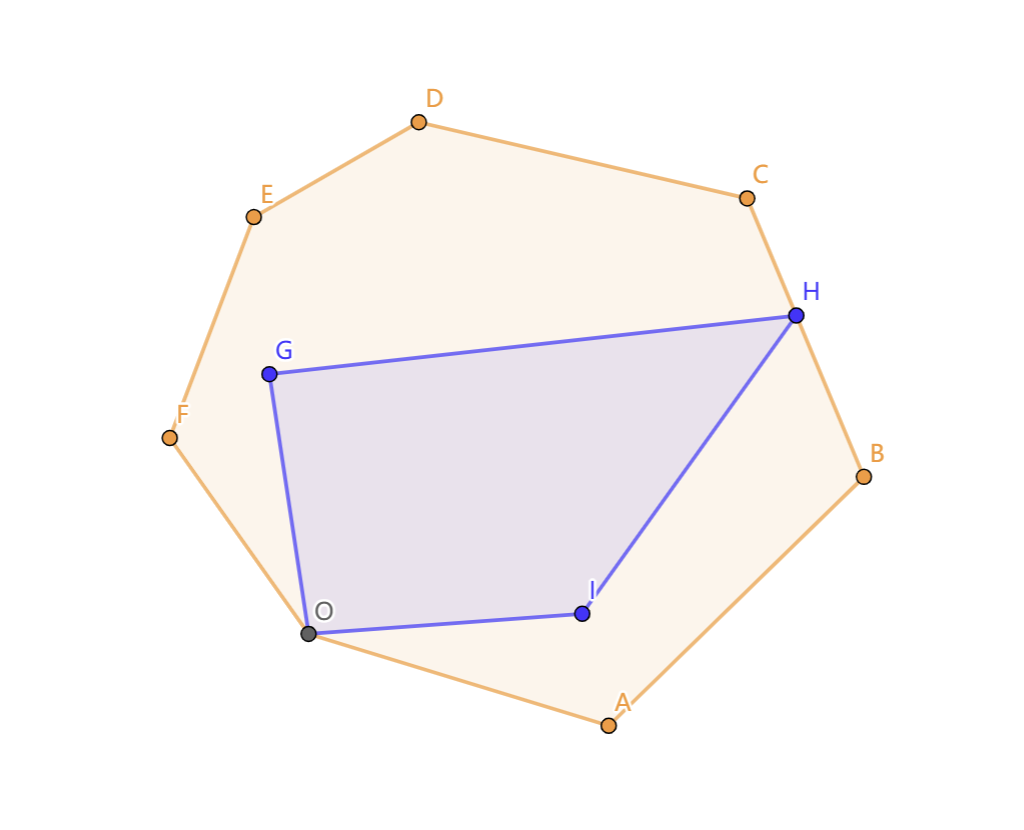
即内层凸包中的点与外层凸包的轮廓重合。判断的方法也很简单，在最开始求外层凸包时，可以先求出非严格凸包。不难发现如果求出来的非严格凸包存在三点共线，那一定是不可能构成包含的局面的，可以直接跳过。

2. 按照极角序分界：

这种情况比较直观，可以参考下图：

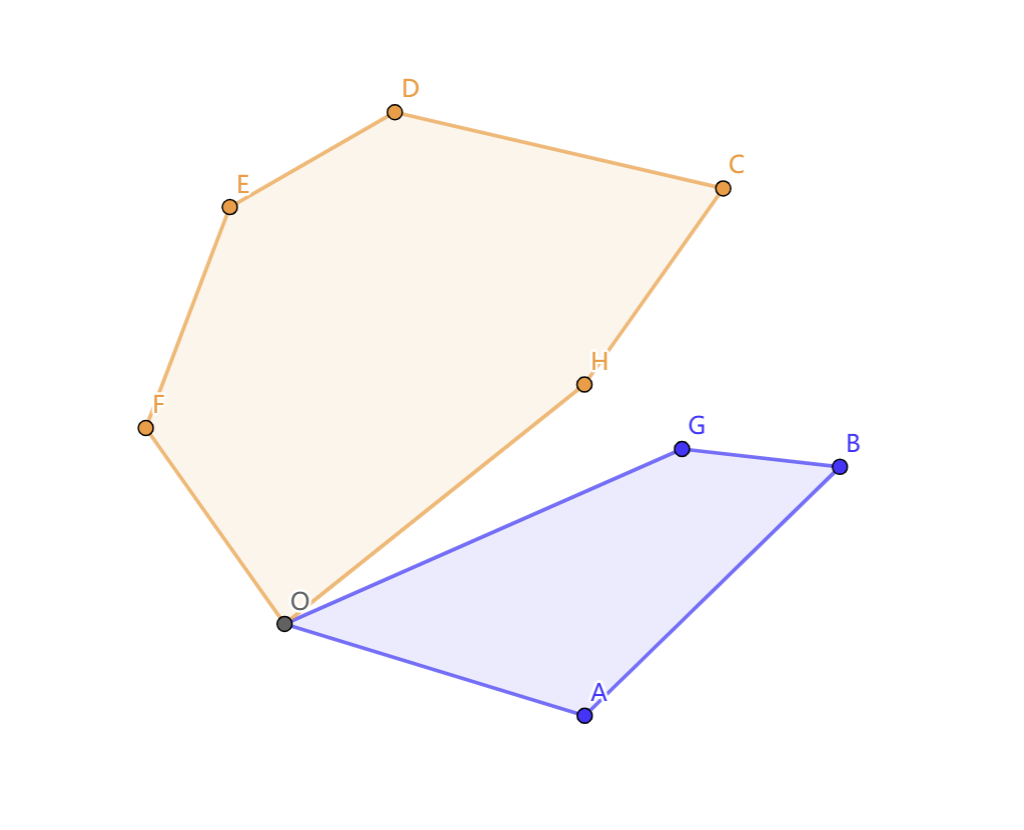
首先把所有点按照极角排序，然后找到相对于 $O$ 的后继（图中为 $A$）按照逆时针的顺序把所有点扫一遍，扫的过程中把点集分成两半并判断两边是否合法，合法则计入答案。

判断合法的方式有很多，我们考虑极角序上相邻的三个点（逆时针顺序）,若其构成的向量为 $\mathbf{u}$ 和 $\mathbf{v}$ 且 $\mathbf{u}\times\mathbf{v}\leq 0$，那么这三个点一定不能在同一个集合中。

当前这种分裂方式只能消耗两组叉乘为负的点，大于两组则当前这种划分方式无解，暴力逐个判断即可，这个方法会在下一个大类中沿用。

第二种情况：$O\notin C_{\mathbb{S}\cup \{O\}}$

这种情况比较棘手，由于被划分的两个集合在按极角排序之后一定是一段连续的区间，故可以考虑旋转卡壳。

先将所有的点按照极角排序，令两个指针 $L,R$ 在点集上移动，$[L,R]$ 中的点划分至 $\mathbb{A}$，剩余的点划分至 $\mathbb{B}$。

考虑对于一个特定的 $L$，$R$ 的取值范围是 $[l,r]$。设 $L$ 的前驱为 $L^\prime$，$R$ 的后继为 $R^\prime$，两个集合分别合法的一个必要条件是 $\angle LOR<180^\circ$ 且 $\angle L^\prime OR^\prime <180^\circ$。

发现 $[l,r]$ 一定是 $\angle L^\prime OL$ 的对顶角划分出来的一段区间。而所有 $L$ 对应的区间都是互不相交且随着 $L$ 单调移动的，所以总的划分方案只有 $\mathcal{O}(n)$ 种。

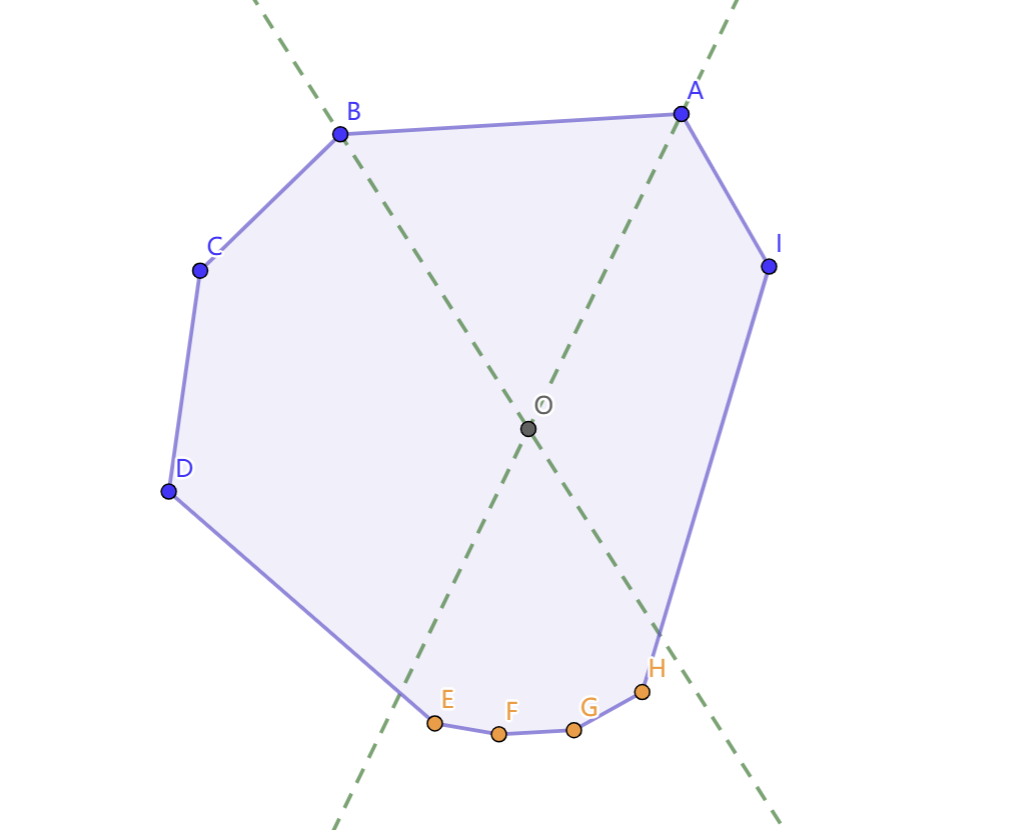
如上图，$B$ 对应的 $[l,r]$ 就是 $\{E,F,G,H\}$，发现这东西很好用旋转卡壳维护，每次扫到一个 $R$ 都考虑把 $L^\prime L$ 和 $RR^\prime$ 断开。

但角度这个条件并不充要，还是得考虑相邻的三元组。所有向量叉乘非正的三元组至多只能有四个（每断一条边至多消耗两个），所以在旋转卡壳的过程中还要判断所有的三元组是否都被消耗。

时间复杂度 $\mathcal{O}(n\log n)$，瓶颈在排序，代码细节较多。

#include<bits/stdc++.h>
#define fi first
#define se second
#define mp make_pair
#define pb push_back
typedef long long ll;
typedef long double ld;
using namespace std;
const int N=500010,M=5000010,INF=0x3f3f3f3f;
const ld eps=1e-6,inf=1e18;
int T,n,m,t,flg,s[N],v[N],w[N],b[N];
ld ans1,ans2;
struct rec{int x,y,z;};
vector<rec> h;

struct node{
	ll x,y;
	node(ll xx=0,ll yy=0){x=xx,y=yy;}
	void in(){scanf("%lld%lld",&x,&y);}
	void out(){printf("%lld %lld\n",x,y);}
}p[N],q[N];

node operator +(node a,node b){return node(a.x+b.x,a.y+b.y);}
node operator -(node a,node b){return node(a.x-b.x,a.y-b.y);}
ll operator *(node a,node b){return a.x*b.x+a.y*b.y;}
ll operator ^(node a,node b){return a.x*b.y-a.y*b.x;}

node operator *(ll x,node b){return node(x*b.x,x*b.y);}

node O(0,0),P(-1,0);
bool cmp1(node a,node b){return a.x!=b.x?a.x<b.x:a.y<b.y;}
bool cmp2(node a,node b){
	if(((a-O)^(b-O))==0){
		if(a*b>0)return a*a<b*b;
		else if((a^P)==0)return a.x<b.x;
		else return (a^P)<(b^P);
	}
    if(((P-O)^(a-O))==0&&(P.x-O.x)*(a.x-O.x)>0)return 1;
    if(((P-O)^(b-O))==0&&(P.x-O.x)*(b.x-O.x)>0)return 0;
    if((((P-O)^(a-O))>0)!=(((P-O)^(b-O))>0))return ((P-O)^(a-O))>((P-O)^(b-O));
    return ((a-O)^(b-O))>0;
}

ld sqr(ld x){return (ld)x*x;}
ld dis(node a,node b){return sqrt(sqr(a.x-b.x)+sqr(a.y-b.y));}

ll chk(node a,node b,node c){
	return (b-a)^(c-b);
}

int pre(int i){return i==1?n:i-1;}
int nxt(int i){return i==n?1:i+1;}

bool check(){
	for(rec t:h)
		if(v[t.x]==v[t.y]&&v[t.x]==v[t.z])return 0;
	return 1;
}
ld solve1(){
	flg=0;
	int cnt=0,tot=0,cur=0;
	ld res=0;
	for(int i=1;i<=n;i++)q[i]=p[i];
	m=n+1;q[m]=node(0,0);
	//outer
	sort(q+1,q+m+1,cmp1);
	for(int i=1;i<=m;i++)v[i]=0;
	s[t=1]=1;
	for(int i=2;i<=m;i++){
		while(t>1&&chk(q[s[t-1]],q[s[t]],q[i])<0)t--;
		s[++t]=i;
	}
	for(int i=1;i<=t;i++){
		if(i>1)res+=dis(q[s[i-1]],q[s[i]]);
		v[s[i]]=1;
	}
	for(int i=1;i<=t;i++)b[++cur]=s[i];
	s[t=1]=1;
	for(int i=2;i<=m;i++){
		while(t>1&&chk(q[s[t-1]],q[s[t]],q[i])>0)t--;
		s[++t]=i;
	}
	for(int i=1;i<=t;i++){
		if(i>1)res+=dis(q[s[i-1]],q[s[i]]);
		v[s[i]]=1;
	}
	for(int i=t-1;i>1;i--)b[++cur]=s[i];
	for(int i=1;i<=m;i++){
		if(v[i]&&!q[i].x&&!q[i].y)w[++cnt]=i,flg=1;
		if(v[i])continue;
		if(!q[i].x&&!q[i].y)return 0;
		w[++cnt]=i;
	}
	//inner
	s[t=1]=w[1];
	for(int i=2;i<=cnt;i++){
		while(t>1&&chk(q[s[t-1]],q[s[t]],q[w[i]])>=0)t--;
		s[++t]=w[i];
	}
	for(int i=1;i<=t;i++){
		if(i>1)res+=dis(q[s[i-1]],q[s[i]]);
		v[s[i]]=2;
	}
	s[t=1]=w[1];
	for(int i=2;i<=cnt;i++){
		while(t>1&&chk(q[s[t-1]],q[s[t]],q[w[i]])<=0)t--;
		s[++t]=w[i];
	}
	for(int i=1;i<=t;i++){
		if(i>1)res+=dis(q[s[i-1]],q[s[i]]);
		v[s[i]]=2;
	}
	for(int i=1;i<=m;i++){
		if(!v[i])return 0;
		tot+=(v[i]==2);
	}
	if(tot<3)return 0;
	for(int i=1;i<=cur;i++)
		if(!chk(q[b[i==1?cur:i-1]],q[b[i]],q[b[i==cur?1:i+1]]))return 0;
	return res;
}
ld solve2(){
	ld res=0,tmp=0;
	h.clear();
	sort(p+1,p+n+1,cmp2);
	for(int i=1;i<=n;i++)v[i]=0;
	for(int i=1;i<=n;i++){
		if(chk(p[pre(i)],p[i],p[nxt(i)])<=0)h.pb((rec){pre(i),i,nxt(i)});
		if(!(p[i]^p[nxt(i)])&&(p[i]*p[nxt(i)])>0)return 0;
	}
	if(h.size()>4)return 0;
	if(flg){
		int flag=0,j=1;
		p[0]=node(0,0);
		for(int i=1;i<=n;i++)
			if((p[i]^p[nxt(i)])<=0)j=nxt(i);
		for(int i=1,k=j;i<=n;i++,k=nxt(k))
			tmp+=dis(p[k],p[nxt(k)]);
		tmp-=dis(p[pre(j)],p[j]);
		tmp+=dis(p[0],p[j]);
		tmp+=dis(p[0],p[pre(j)]);
		v[j]=1;j=nxt(j);
		for(int i=2;i<n-1;i++,j=nxt(j)){
			v[j]=1;
			if(!check())continue;
			flag=1;
			res=max(res,tmp+dis(p[0],p[j])+dis(p[0],p[nxt(j)])-dis(p[j],p[nxt(j)]));
		}
		if(flag)return res;
		return 0;
	}
	for(int i=1;i<=n;i++)tmp+=dis(p[i],p[nxt(i)]);
	v[1]=1;
	for(int i=1,j=1,k=1;i<=n;i++,k--){
		while((p[i]^p[nxt(j)])>0){
			j=nxt(j),v[j]=1,k++;
			if(!check()||n-k<2||(p[nxt(j)]^p[pre(i)])<=0)continue;
			res=max(res,tmp-dis(p[pre(i)],p[i])-dis(p[j],p[nxt(j)])
				+dis(p[0],p[i])+dis(p[0],p[j])+dis(p[0],p[pre(i)])+dis(p[0],p[nxt(j)]));
		}
		v[i]=0;
	}
	return res;
}
void solve(){
	scanf("%d",&n);
	for(int i=1;i<=n;i++)p[i].in();
	ans1=solve1();
	ans2=solve2();
	printf("%.10Lf\n",max(ans1,ans2));
}
int main(){
	scanf("%d",&T);
	while(T--)solve();
	return 0;
}